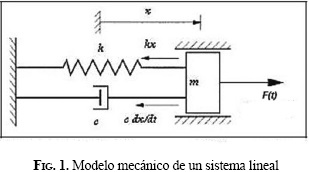
Implementación de una estrategia fuzzy adaptativa para el control activo de vigas vibratorias

Implementation of a Fuzzy Adoptive Strategy for Active Vibration Control of Beams

Francisco Ernesto Moreno-García*
José Armando Becerra-Vargas**
Edwin Martín Cárdenas-Contreras***

* Ph.D. Universidad Francisco de Paula Santander (San José de Cúcuta-Norte de Santander, Colombia). femgarcia@ufps.edu.co
** M.Sc. Universidad Francisco de Paula Santander (San José de Cúcuta -Norte de Santander, Colombia). josearmandobv@ufps.edu.co
*** Universidad Francisco de Paula Santander (San José de Cúcuta -Norte de Santander, Colombia). emc_ed@hotmail.com

Fecha de Recepción: 26 de Diciembre de 2013 Fecha de Aprobación: 24 de Enero de 2014

Resumen

Este trabajo propone un control activo de vibraciones en un sistema mecánico tipo viga en voladizo, utilizando un controlador fuzzy implementado en LabVIEW. Para la etapa de medición se utiliza un acelerómetro capacitivo capaz de detectar el desplazamiento presentado en la estructura debido a una fuerza generada mediante un impactador instrumentado con un sensor piezorresistivo. Para la implementación computacional es utilizado el software LabVIEW operando en conjunto con una tarjeta de adquisición de datos DAQ 6009. Para el sistema de actuación se ubican en la barra láminas de material piezoeléctrico, que tienen la función de atenuar la vibración presente mediante la generación de fuerzas opuestas. Los resultados experimentales se presentan con el objetivo de acumular experiencias y demostrar la eficacia del control activo de vibraciones con la utilización de actuadores piezoeléctricos.

Palabras clave: Control Activo de Vibraciones, Lógica Fuzzy, Material piezoeléctrico, Viga en Voladizo.

Abstract

This paper proposes an active control of vibrations in a mechanical system type beam cantilever using a Fuzzy controller implemented in LabVIEW. In the step of measuring a capacitive accelerometer is used to detect the displacement introduced in the structure due to a force generated by the impactor instrumented with piezoresistive sensor. For computational implementation is used LabVIEW software operating in conjunction with a DAQ 6009 acquisition card data. For actuation system are located in the sheet bar of piezoelectric material which has the function to attenuate the present vibration through the generation of opposing forces. The experimental results are presented with the objective of to gain experience and demonstrate the efficacy of the active control of vibrations using piezoelectric actuators.

Keywords: Active Vibration Control, Fuzzy Logic, Piezoelectric Material, Cantilever Beam.

I. Introducción

Los problemas estructurales debido a las vibraciones mecánicas son comunes en estructuras flexibles; de hecho, todas las estructuras pueden considerarse flexibles, desde que experimenten cierta deformación bajo el efecto de cualquier carga, no importa cuán pequeña sea. Las estructuras flexibles se pueden encontrar en maquinaria, aviones, vehículos y construcciones civiles. La mayoría de las vibraciones mecánicas son indeseables, porque pueden causar ruido, tensiones en la estructura y mal funcionamiento o fallos del sistema del cual forman parte. En los últimos años, con la creciente necesidad de equipos cada vez más fiables, el estudio y control de las vibraciones mecánicas ha sido de gran interés en proyectos de ingeniería, con el fin de evitar fracasos.

A pesar del daño que pueden causar las vibraciones en sistemas mecánicos, también se pueden utilizar para diversas aplicaciones en la industria de consumo. Algunos ejemplos industriales donde se aplican vibraciones son: cintas transportadoras, cribas vibratorias y tolvas. También está la aplicación de vibraciones en los procesos de mecanizado tales como mecanizado ultrasónico, forja y fundición [1].

La mecatrónica y las estructuras adaptativas abarcan un campo muy extenso que comprende aplicaciones tales como la cancelación de vibraciones y ruidos, aumento de la estabilidad aeroelástica, cambio de la forma de la estructura o distribución de esfuerzos. Ello está originando líneas de investigación relacionadas con el desarrollo y estudio de nuevos materiales para la construcción de estructuras, producción de nuevos sensores y actuadores e implementación de nuevas técnicas de control [2].

II. Marco teórico

A. Vibraciones Mecánicas

El estudio de las vibraciones mecánicas, también llamado mecánica de las vibraciones, es una rama de la mecánica que estudia el movimiento oscilatorio de los cuerpos, y de las fuerzas asociadas con él; se debe tener presente que los términos movimiento, oscilación y vibración no son sinónimos, pues toda vibración es una oscilación y toda oscilación es un movimiento, pero no se puede presentar en sentido inverso. Tanto las oscilaciones como las vibraciones se propagan en el tiempo mediante un proceso de cambios entre los distintos tipos de energía, pero la diferencia radica en que la oscilación es un intercambio de energía tanto cinemática como potencial gravitacional, a diferencia de las vibraciones mecánicas, en las cuales se encuentra presente la energía de deformación o la energía potencial elástica [3].

Los sistemas estructurales, como los sistemas robóticos, edificios civiles, vehículos de transporte, artículos deportivos, etcétera, a menudo están sujetos a excitaciones externas e internas que provocan vibraciones no deseadas, poniendo en peligro la integridad estructural del propio sistema y, en algunos casos, incluso la salud de las persona. En la actualidad se observa en gran crecimiento la demanda de estos sistemas, entre los que se encuentran:

-Necesidad de estructuras más ligeras y fuertes, en el caso de los medios móviles, ocasionando un ahorro en el consumo de combustible, o en el caso de los mecanismos robóticos, donde se necesita la operación bajo par de torsión.

-Excelente comportamiento dinámico para garantizar la estabilidad del sistema y la precisión del movimiento, en sistemas con dispositivos ligeros, reducción de fallo por fatiga, que puede lograrse reduciendo al mínimo la vibración, y mejora de la calidad de las estructuras mecánicas.

B. Características de un sistema vibratorio

En general, un sistema que experimenta vibraciones tiene cuatro características básicas:

Las vibraciones mecánicas pueden clasificarse desde diferentes puntos de vista, dependiendo de: a) la excitación, b) la disipación de energía, c) la linealidad de los elementos.

-Vibración libre: Es la que ocurre cuando un sistema oscila bajo la acción de fuerzas inherentes al sistema mismo, es decir, cuando no actúa ninguna fuerza externa. El sistema bajo vibración libre vibrará a una o más de sus frecuencias naturales, que son propiedades del sistema dinámico que dependen de su distribución de masa y de rigidez.

-Vibración forzada: Es la que ocurre cuando la vibración tiene lugar bajo la excitación de fuerzas externas. Cuando la excitación es oscilatoria, el sistema es obligado a vibrar a la frecuencia de excitación. Si esta coincide con una de las frecuencias naturales del sistema, se produce una situación de resonancia y ocurren oscilaciones peligrosamente grandes.

El amortiguamiento es un sinónimo de la pérdida de energía de sistemas vibratorios, y se manifiesta con la disminución del desplazamiento de la vibración; este hecho puede aparecer como parte del comportamiento interno de un material, por ejemplo, la fricción, o como un elemento físico, llamado precisamente amortiguador.

Por lo tanto, la vibración amortiguada es aquella en la que la frecuencia de oscilación de un sistema se ve afectada por la disipación de la energía, pero cuando la disipación de energía no afecta considerablemente la frecuencia de oscilación, la vibración es del tipo no amortiguada.

D. Controly atenuación de vibraciones

En la práctica, los sistemas de control que utilizan vibraciones mecánicas pueden ser clasificados como de control pasivo, de control activo o híbridos.

Típicamente, el control activo de vibración consiste en cancelar un disturbio mediante la adición de una señal igual o cercana en magnitud, pero el efecto es opuesto. Este tipo de control utiliza fuentes de energía externa al sistema para generar un esfuerzo de control; en otras palabras, una fuerza en la dirección opuesta para aliviar la respuesta de la estructura. Ejemplos de sistemas de control activo de vibraciones se pueden encontrar en [4]. En la Fig. 2 se ilustra el plan de control activo y pasivo.

El control pasivo incluye la aplicación de equipo mecánico para disipar energía en forma de vibraciones generadas en la estructura, es decir, una forma de atenuar la respuesta estructural y también reducir los posibles daños a las estructuras. Estos sistemas tienen características que no requieren alimentación externa para funcionar ni mediciones en la respuesta del sistema [5], [2]. Algunos de los equipos utilizados para disipar esta energía son amortiguadores de fricción en seco, amortiguadores de líquido sintonizado, amortiguadores de masa sintonizados y material viscoso líquido, y amortiguadores viscoelásticos. Desventajosamente, este tipo de control tiene una banda de frecuencias de operación limitada, como, por ejemplo, amortiguadores de líquido sintonizado y masa sintonizada, que son muchas veces para el primer modo de vibración.

Una manera simple, económica y que presenta buenas perspectivas en el área de vibraciones es trabajar con elementos piezoeléctricos; estos materiales son comúnmente llamados "materiales inteligentes" [6-9], debido a su habilidad de medir y contrarrestar vibraciones mecánicas para diferentes tipos de estructuras como barras, placas y armaduras. Investigaciones sobre "estructuras inteligentes" exige conocimiento en áreas tales como ciencia de los materiales, mecánica estructural, electrónica, procesamiento de señales, matemáticas y control.

III. Banco experimental

Cualquier estructura que sufre algún tipo de deformación bajo el efecto de una carga se considera flexible; así, la estructura física utilizada en las pruebas (Fig. 3) fue de una barra flexible tipo viga en voladizo. La elección de este tipo de estructura se debe al hecho de que muchos sistemas estructurales pueden ser modelados como una barra en voladizo, como álabes de turbinas y estructuras de robots.

La viga es instrumentada por un acelerómetro capacitivo MMA7361L colocado a 30 cm. del lado empotrado, en donde se considera teóricamente la influencia del primer modo de vibración; para el control propuesto solo se atenuarán vibraciones ocurridas en el primer modo. Los datos obtenidos por el acelerómetro son enviados a la tarjeta de adquisición de datos "DAQ 6009" para procesamiento en el software LabVIEW 2012, donde es implementado el controlador fuzzy con mecanismo de adaptación. Este sistema de monitoreo y control se encarga de adquirir los datos enviados desde el acelerómetro, calcular la señal de control y generar una señal de salida tipo senoidal que luego es acondicionada para alimentar los actuadores piezoeléctricos tipo BA4510.

A. Análisis de Frecuencia Natural de Vibración

El ensayo experimental para las frecuencias naturales de la viga se obtiene a partir del análisis de respuesta en frecuencia en el software LabVIEW 2012 con la herramienta (FFT Spectrum (Mag-Phase)). Para determinar estas frecuencias se utiliza la señal proveniente del acelerómetro capacitivo instalado en el extremo libre de la viga. El sistema es perturbado por el martillo de impacto instrumentado con el sensor FSR-01.

A partir de la Fig. 4 es posible obtener el valor de la primera frecuencia natural de la estructura con el elemento piezoeléctrico incorporado, aplicando una fuerza de 4N; este valor es de 5.8 Hz.

IV. Controlador fuzzy adaptativo

La necesidad de identificar cambios y de adaptarse a nuevas condiciones adiciona a los controladores fuzzy adaptativos dos componentes extras, que no están presentes en los controladores fuzzy convencionales [10]. El primer componente es el "monitor de procesos", que detecta los cambios en las características del proceso; este monitoreo puede ser hecho de dos maneras: midiendo el desempeño del sistema sobre el control o estimando continuamente algunos parámetros del modelo del proceso. El segundo componente responsable es el "mecanismo de adaptación"; este mecanismo puede modificar los parámetros del controlador para mejorar el desempeño con base en las salidas del monitor de proceso. La Fig. 5 muestra el esquema general de un controlador fuzzy adaptativo tipo con sus componentes.

Para realizar el control del sistema con base en la información anteriormente presentada fue usado, inicialmente, un controlador fuzzy principal (convencional), y enseguida fue implementado un mecanismo fuzzy de adaptación de ganancia. El diagrama de bloques del controlador fuzzy principal (convencional) es mostrado en la Fig. 6.

Fueron definidas para cada una de las entradas del controlador fuzzy principal tres funciones de pertinencia [(N)egativo, (Z)ero e (P)ositivo] del tipo triangular e igualmente espaciadas y definidas dentro de un universo del discurso sintonizados de forma heurística. La salida del controlador fuzzy es de tipo sugeno de orden cero, con valores "crisp" (N=-1.0, Z=0 y P=1.0) constantes. El mecanismo de inferencia utilizado fue el max-prod.

La definición de las variables de entrada del controlador Fuzzy es evaluada a partir de la señal de error y de la variación del error, definidas por las siguientes ecuaciones:

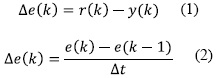
Donde k y Δt se refieren al instante y al intervalo de tiempo utilizados; y(k) es la lectura del sensor de aceleración.

Una vez proyectado el controlador principal, el segundo paso fue la adición del mecanismo de adaptación; para eso, el universo del discurso del controlador principal fue normalizado en un intervalo de -1 a 1, y acoplado al controlador fuzzy principal. El mecanismo fuzzy de adaptación de la ganancia se muestra en la Fig. 7.

Cabe destacar que el sistema es monitoreado a partir de la media absoluta derivada del error y de la media absoluta de la salida de control, observando los tres últimos tiempos de muestreo; estos valores son calculados de la siguiente forma:

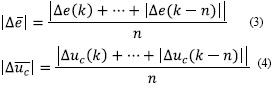
De forma similar al controlador fuzzy, fueron definidas para cada una de las entradas del mecanismo fuzzy de adaptación tres funciones de pertinencia [(P-pequeño, (M-medio e (G-grande] de tipo triangular, definidas dentro del universo de discurso de las variables de entrada y sintonizadas de forma heurística, como lo ilustra la Fig. 8. El mecanismo de inferencia fue max-prod y de salida de tipo Sugeno de orden cero.

A. Respuesta en malla abierta

Para realizar los ensayos con el objetivo de evaluar el desempeño del controlador lógico difuso adaptativo, el sistema es operado inicialmente en malla abierta (sin control). El ensayo al sistema en malla abierta sin controlador se realiza experimentalmente con una excitación de naturaleza impulsiva F=4N, aplicado a unos 24 cm. del extremo libre; a partir de ese instante el sistema oscila libremente y muestra un comportamiento poco amortiguado del sistema, destacando el tiempo de acomodamiento en (12s). En la Fig. 8 se ilustra este comportamiento.

B. Desempeno del controlador fuzzy con mecanismo de adaptación

El mecanismo de adaptación es de naturaleza fuzzy y tiene dos entradas provenientes del mecanismo de monitoreo: la media absoluta de la derivada del error |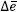| y la media absoluta de la salida de control |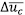| . De forma similar al controlador fuzzy principal, son definidas funciones de pertinencia para cada una de estas entradas, suponiendo tres funciones (pequeño, medio, grande) de tipos triangulares, igualmente espaciadas y definidas dentro de un universo de discurso apropiado. Las salidas son funciones de pertinencia que representan la acción deseada para el factor de escala, y serían:

(Aumentar Kv (Kv = 1.2)), (mantener Kv (KKv = 1)), (disminuir Kv (KKv = 0.8)), conforme se muestra en la Fig. 9.

Se puede decir heurísticamente que:

  1. Si |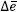| es grande y |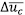| es pequeño, entonces es preciso aumentar el valor de control. Esto puede ser obtenido aumentando la sensibilidad de la variación de error del controlador fuzzy principal, o sea, aumentando Kv.

  2. Si |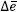| es grande y |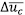| es grande, entonces es preciso disminuir el valor de control. Esto puede ser obtenido disminuyendo la sensibilidad de la variación de error del controlador fuzzy principal, o sea, disminuyendo Kv.

  3. Si |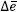| es pequeño y |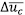| es pequeño, entonces Kv se mantiene.

El procedimiento de adaptación propuesto requiere del inicio del factor de escala Kv conforme a la ecuación (5). Al admitir una condición inicial de grandes perturbaciones, la evolución de Kv a lo largo del proceso debe permitir un crecimiento gradual del esfuerzo de control. Por lo tanto, debe comenzar pequeño (baja sensibilidad en la entrada), lo que conduce a que el esfuerzo inicial de control sea también pequeño. El controlador adaptativo de factor de escala, observando las condiciones iniciales de error elevado y pequeña señal de control, actúa para aumentar la sensibilidad del controlador fuzzy principal, aumentando el factor de escala Kv por medio de la salida KKv [11].

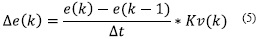
Cuando el sistema converge en una situación de baja señal de entrada y baja señal de control, el valor de Kv prácticamente es constante (KKv≈1). Ahora, si hay una perturbación que provoque un aumento de error, el algoritmo de adaptación, tal como se propuso, aumenta el valor de Kv (a través de KKv), que podría dar lugar a una divergencia en el controlador. Para hacer frente a esto, se propone que una vez detecta las condiciones de equilibrio (KKv cerca de la unidad durante cierto tiempo) debe disminuir el valor del factor de escala para el nivel de inicio. Si esto se hace y la señal de control es aún pequeña y el sistema está abierto a nuevas perturbaciones, los siguientes pasos deben garantizar el correcto funcionamiento del algoritmo:

-Inicio Kv con un valor pequeño que garantice baja señal de control, por ejemplo, Kv=1/1000.

-Comprobar si el sistema ha alcanzado el estado de equilibrio.

-Si durante las últimas N muestras el valor de KKv permanece en la faja de 1, N=20 y δ=1, por ejemplo.

-Si se alcanzó el régimen permanente, reiniciar el valor de Kv.

Esta formulación heurística para un controlador fuzzy adaptativo de factor de escala será objeto de estudio, comprobando su funcionamiento para el control activo de vibraciones mecánicas.

Las pruebas 1 y 2 muestran el comportamiento del sistema mecánico tipo viga en voladizo, realizando una comparación con las respuestas obtenidas en diferentes ensayos en los que se aplica una fuerza igual y otra fuerza mayor a la del sistema libre, como se muestra en la Tabla 1.

En la Fig. 10 se observa que el sistema es controlado aproximadamente en 8s, implicando un nivel de atenuación satisfactorio comparado con los 12s del sistema libre.

También se observa en la Fig. 11 la señal de control inicialmente pequeña (debido a un bajo desplazamiento) y va aumentando a medida que la viga oscila libremente; a medida que el sistema se amortigua, el valor de la señal de control disminuye notablemente.

En la prueba 2 se muestra el comportamiento del sistema con mecanismo de adaptación fuzzy al aplicar una fuerza mayor a la utilizada en el sistema libre mostrado en la Fig. 8.

En la Fig. 12 se observa que el sistema es controlado aproximadamente en 10s cuando se aplica una fuerza mayor (F2), implicando un nivel de atenuación aún mayor para desplazamientos mayores, comparado con los 8s de respuesta para la fuerza F1 y los 12s del sistema libre.

Ahora, para el caso cuando se presenta una gran fuerza de impacto que consecuentemente generó un gran desplazamiento, se observa que el tiempo de acomodamiento tiene una estabilización semejante al sistema libre sin controlador, lo cual indica la eficiencia del controlador, debido a que el valor de desplazamiento se mantiene superior al valor definido para el universo de discurso del controlador fuzzy principal; esto se debe a que la señal de control se limita al valor máximo, provocando una excitación mayor en los actuadores piezoeléctricos, la cual logra que el sistema se estabilice más rápidamente, como se muestra en la Fig. 13.

V. Conclusiones

La fuerza aplicada a cada uno de los ensayos realizados se encuentra en un rango no mayor a 10N, debido a que una fuerza mayor podría ocasionar el daño en el material resistivo ubicado en el área activa del sensor tipo FSR. El sensor FSR no es un medidor de deformación, célula de carga o transductor de presión. Si bien se puede utilizar para la medición dinámica, solo son, generalmente, obtenibles resultados cualitativos. La precisión de la fuerza varía de aproximadamente ± 5% a ± 25%, dependiendo de la consistencia del sistema de medición y la tolerancia repetitiva en la fabricación.

La frecuencia natural de vibración en la barra metálica aumenta su valor si su longitud efectiva es relativamente corta.

Para efectuar una correcta medición es necesario que la barra de prueba se encuentre ajustada firmemente en el soporte, pues si éste no es el caso se producirán vibraciones en este punto y se obtendrán resultados erróneos.

El análisis de vibración es una herramienta muy útil para evaluar la resistencia de materiales que serán usados en aplicaciones críticas.

Los controladores basados en lógica fuzzy para atenuar las vibraciones mecánicas no deseadas son una herramienta muy potente basada en el conocimiento heurístico del sistema.

No fue necesario desarrollar un modelo matemático para el comportamiento dinámico del sistema, y la comprensión intuitiva fue muy valiosa, sobre todo en la elaboración de la base de reglas.

Seguramente el tiempo de desarrollo de este controlador fue menor que el desarrollo de los clásicos controladores convencionales.

El controlador fuzzy adaptativo, alterando el factor de escala (Kv), así como el mecanismo de adaptación presentados en este trabajo es adecuado para el control en tiempo real, y tiene una fuerte capacidad de autosintonización para el rango de variables de entrada usando el error medio de la señal de control y el cambio en el error como índice de desempeño.

Referencias

[1] S. Rao, Vibraciones Mecánicas (quinta edición), Pearson Education, Inc. Prentice Hall, 744 p, 2011.

[2] I. Chopra, Review of state-of-art of smart structure and integrated systems. AIAA Journal, 40(11): 2145-2187, 2002.

[3] M. R. Pallares and W. C. Rodríguez, Modelación del fenómeno de vibración forzada formulando una analogía eléctrica con el programa de elementos finitos "Ansys". Revista Ingeniería e Investigación, ISSN: 0120-5609. Universidad Nacional de Colombia, 2005.

[4] P. H. Palma, Identificação Experimental e Controle Ativo de Vibrações Aplicadas em Estruturas Inteligentes, UNESP, Brasil, 2007.

[5] F. Cheng et al., Smart Structures. Innovative systems for seismic response control. 2008.

[6] T. Manjunath and B. Bandyopadhyay, Smart Control of cantilever structures using output feedback. International Journal of Simulation, Systems, Science & Technology. Oxford. EE.UU. 2006.

[7] P. Naucler, Modeling and control of a viscoelastic piezolaminated beam. In: IFAC World Congress, Prague. Proceedings Oxford, 2005.

[8] V Sethi and G. Song, Multimode optimal vibration control of flexible structure using piezoceramics. In: International Symposium on Intelligent Control. Taipei. Proceedings New York, EE.UU, 2004.

[9] G. Taylor, J. Gagnepain, T. Meeker, T. Nakamura, L. Shuvalov, Piezoelectricity. Gordon and Breach Science Publishers. New York, 1985.

[10] I. Cárdenas, Uso de controladores fuzzy adaptativos implementados em microcontroladores, no controle de vibrações de sistemas mecánicos. Dissertação de Mestrado. Universidade Federal de Uberlándia, Brasil, 2001.

[11] F. E. Moreno-Garcia, Avaliação Teórico-Experimentalde Técnicas de Controle Fuzzy Aplicadas a Sistemas de Refrigeração. Universidade Federal Uberlándia. Brasil, 2010.