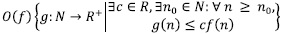
Eficiencia algorítmica en aplicaciones de grafos orientadas a redes GMPLS

Efficiency Graphs fllgorithmic's applications oriented to GMPLS networks

Simar Enrique Herrera-Jiménez^*
Octavio José Salcedo-Parra^**
Adriana Patricia Gallego-Torres^***

^* Universidad Distrital Francisco José de Caldas (Bogotá, Cundinamarca - Colombia). seherreraj@udistrital.edu.co
^** Ph.D. Universidad Distrital Francisco José de Caldas (Bogotá, Cundinamarca - Colombia). osalcedo@udistrital.edu.co
^*** Ph.D. Universidad Distrital Francisco José de Caldas (Bogotá, Cundinamarca - Colombia). adpgallegot@udistrital.edu.co

Fecha de Recepción: 06 de Enero de 2014 Fecha de Aprobación: 31 de Enero de 2014

Resumen

Los algoritmos utilizados en el desarrollo y aplicación de grafos hacen uso de recursos medibles en tiempo y espacio; al estudio de estos costos se le conoce como complejidad algorítmica; frecuentemente se hace uso de cualquier algoritmo al azar sin realizar un análisis de ellos en el ambiente en que se ejecutarán; el objetivo del presente artículo es hacer un análisis algorítmico en ambientes comunes, con el fin de generar estadísticas que evidencien la conveniencia del uso de algoritmos específicos.

Palabras clave: Algoritmo, Complejidad algorítmica, Grafo.

Abstract

The algorithms applied in the graphs' development and application, use measurable sources in time and space. This subject costs' study is called algorithmic complexity. Frequently algorithms are used at random, without any environmental analysis, in which they will be executed. The present paper's objective is to make an algorithmic analysis on different common environments, with the purpose to generate information sources, which can show the convenience to use any specific algorithm.

Keywords: Algorithm Complexity, Graph, Efficiency Optimization.

I. Introducción

Para trabajar con algoritmos relacionados con grafos y sus aplicaciones es necesario tomar en cuenta las ramas de las ciencias de la computación que prestan herramientas para realizar análisis detallado, describiendo medidas en tiempo y espacio, para evaluar la eficiencia de éstos.

II. Análisis algorítmico

El análisis algorítmico se puede definir como el estudio que se realiza sobre un algoritmo para determinar si su rendimiento y comportamiento cumple con los requerimientos [15]; adicionalmente, permite tomar en cuenta esta información para determinar la eficiencia del algoritmo. El objetivo del análisis de algoritmos es cuantificar las medidas físicas: "tiempo de ejecución y espacio de memoria" y comparar distintos algoritmos que resuelven un mismo problema [2]. En el análisis de algoritmos es necesario tener en cuenta, inicialmente, que los algoritmos construidos deben ser correctos, es decir, deben producir un resultado deseado en tiempo finito. Los criterios para realizar esta evaluación pueden ser eficiencia, portabilidad, eficacia, robustez, etc. [3]. El concepto de eficiencia de un algoritmo es relativo, dado que ante dos algoritmos que resuelven el mismo problema, uno es más eficiente que otro si consume menos recursos, presentándose que algunos dan una eficiencia en tiempo, pero con un consumo alto de recursos, o, por el contrario, un uso óptimo de recursos, pero con un tiempo un poco más largo. De acuerdo con esto, en muchas ocasiones es bastante útil predecir cómo se comportará un algoritmo sin llegar a su implementación, es decir, analizar el algoritmo matemáticamente.

III. Complejidad algorítmica

La teoria de la complejidad computacional es la parte de la teoría de la computación que estudia los recursos requeridos durante el cálculo para resolver un problema [16]. Dado que en las ciencias de la computación los algoritmos son la herramienta más importante que se presenta, deben dar solución a diferentes problemas, con pasos concretos, claros y finitos. Cada algoritmo arroja un cálculo correcto a través de la recepción de datos de entrada y de la generación de información de salida [5]. El análisis de complejidad de un algoritmo produce como resultado una "función de complejidad" [21], que da una aproximación del número de operaciones que realiza [17]. Cada algoritmo se puede medir en tiempo y espacio, un algoritmo será más eficiente comparado con otro, siempre que consuma menos recurso, como el tiempo y el espacio necesarios para ejecutar; para esto se realizan ciertas operaciones matemáticas que identifican la eficiencia teórica del programa; a estos estudios se les denomina complejidad algoritmica [2].

A. Notación asintótica

Dentro del análisis de complejidad existen factores constantes que son poco relevantes y pueden ser omitidos en la comparación de tasas; para tal fin se utiliza la notación asintótica [6]. La eficiencia de un algoritmo se puede definir como una función t(n) [20]. Al analizar un algoritmo, lo relevante es el comportamiento cuando se aumenta el tamaño de los datos; esto se conoce como eficiencia asintótica de un algoritmo. Para describir la notación asintótica se hace uso de las matemáticas, definiéndola como función para cual los números naturales N son su dominio [1].

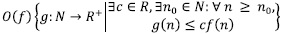
Algunas reglas sobre esta notación son las siguientes [8]:

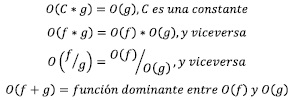
B. Divide y vencerás

Divide y vencerás es una técnica de diseño de algoritmos que consiste en resolver un problema a partir de la solución de subproblemas del mismo tipo, pero de menor tamaño. Si los subproblemas son todavia relativamente grandes se aplicará de nuevo esta técnica hasta alcanzar subproblemas lo suficientemente pequeños para ser solucionados directamente; ello, naturalmente, sugiere el uso de la recursión en las implementaciones de estos algoritmos [7]. La resolución de un problema por medio de esta técnica se da a través de, mínimo, los siguientes pasos:

1. División: Identificar los subproblemas del mismo tipo del problema original y organi-zarlos en los diferentes grupos, k.

2. Solución subproblemas: Deben solucionarse de manera independiente todos los subproblemas que estrictamente son de me

3. Solución problema: Dada una solución de los subproblemas, articular estas soluciones para construir la solución del problema en general.

C. Ordenes de complejidad

Utilizando la notación asintótica, podemos definir un "orden de complejidad" básico [8]; de esta forma enumeramos lo siguiente:

D. Recurrencias

En argumentos lógicos o en algoritmos se presenta la necesidad de resolver una sucesión de casos, para lo cual, a nivel matemático, normalmente se busca estructurar la conexión de cada caso con el anterior. La recurrencia es un método astuto que busca enlazar cada caso con el anterior, es decir, generalizar el procedimiento y que al resolver solo el último caso nos permita encontrar la respuesta de los demás, es decir, al final solo nos quedará un primer caso por resolver, del que se deducirán todos [9]. En algunos ejemplos se encuentra el cálculo de series, sucesiones o recorridos, que inicialmente son problemas iterativos, pero a través del estudio o análisis de complejidad, es posible plantear una ecuación de recurrencia; uno de los ejemplos nombrados y conocidos es el cálculo de la serie de Fibonacci: 1-1-2-3-5-813-21-...

Dentro del manejo dado a las ecuaciones de recurrencia, al llevarlas a un proceso algoritmico aparece una restricción, consistente en que mientras se resuelve el último caso, todo el proceso está haciendo uso de un gran espacio de memoria y genera conflictos en ejecución; por tal motivo, antes de hacer uso de esta técnica siempre es necesario tener presente esto y tomar la decisión de combinarla con otros métodos de solución o presentar otra posible solución desde el principio.

IV. Programación dinámica

Cuando se trabaja con algoritmos que buscan optimizar procesos, y más aún cuando se trabaja con algoritmos de representación en grafos, generalmente después de realizar el análisis correspondiente se encuentra que hay necesidad de utilizar un método más avanzado, por tal motivo se hace uso de la programación dinámica [22], que es un método general de optimización de procesos de decisión por etapas, adecuado para resolver problemas cuya solución puede caracterizarse recursivamente y en la que los subproblemas que aparecen en la recursión se solapan de algún modo, lo que significaria una repetición de cálculos inaceptable si se programa la solución recursiva de manera directa [10].

En ocasiones, las soluciones presentadas por otros métodos divisan un inconveniente, esto es, cuando cada uno de los subproblemas se solapan entre si, impidiendo la solución de forma independiente de cada uno de ellos, mostrando que la recursividad no resulta eficiente por la repetición de cálculos que conlleva; en estos casos, la programación dinámica ofrece una solución aceptable; la eficiencia de esta técnica consiste en resolver los subproblemas una sola vez, guardando las soluciones para su futura utilización [10].

Aplicar la programación dinámica no solo tiene sentido por razones de eficiencia, sino porque además presenta un método capaz de resolver de manera eficiente problemas cuya solución ha sido abordada por otras técnicas y ha fracasado [19]. La programación dinámica tiene mayor aplicación en la resolución de problemas de optimización, que, generalmente, presentan distintas soluciones, y lo que busca esta técnica es encontrar la solución de valor óptimo. La solución de problemas mediante esta técnica se basa en el llamado principio óptimo enunciado por Bellman en 1957: "En una secuencia de decisiones óptimas, toda sub-secuencia ha de ser también óptima" [7].

En grandes líneas, el diseño de un algoritmo de programación dinámica consta de los siguientes pasos:

1. Planteamiento de la solución como una sucesión de decisiones y verificación de que cumple el principio de óptimo.

2. Definición recursiva de la solución.

3. Cálculo del valor de la solución óptima mediante una tabla en donde se almacenan soluciones a problemas parciales para reutilizar los cálculos.

4. Construcción de la solución óptima haciendo uso de la información contenida en la tabla anterior.

A. Funciones con memoria

En la programación dinámica, la solución se basa en tener la solución de pequeños subproblemas más grandes, construyendo un árbol que nos lleve a la solución general del problema [10].

V. Algoritmos de grafos

Generalmente, el diseñador del algoritmo, o programador, busca que cada función sea resuelta de forma eficiente, y a través del análisis, que se puede realizar de la forma descrita en el presente documento, definir cuál es el método por utilizar. Al afrontar problemas que tienen una necesidad de optimización y cuya estructura se puede definir como un grafo cualquiera, la combinación del desarrollo de estructuras de datos, algoritmos de recorridos, algoritmos de búsquedas y la programación dinámica indican una cantidad de algoritmos ya estudiados y utilizados por su optimalidad. Dentro de esos algoritmos se encuentran los siguientes [11]:

1. Algoritmo de Dijkstra: Orden de complejidad; orden que genera una respuesta que en problemas complejos de este tipo tiene un tiempo de ejecución de no más de 1 segundo.

2. Algoritmo de Kruskal: Orden de complejidad.

3. Algoritmo de Floyd-Warshall: Orden de complejidad.

4. Algoritmo de Prim: Orden de complejidad .

5. Algoritmo de Bellman-Ford: Orden de complejidad.

6. Algoritmo de Ford-Fulkerson: Orden de complejidad.

Cada algoritmo de estos presenta un excelente rendimiento en determinado ámbito, por lo que lo ideal es conocer cuál es el ámbito en el que funciona mejor cada uno de ellos.

A. El algoritmo de Dijkstra

En la complejidad, uno de los clásicos problemas es encontrar la ruta más corta entre un vértice inicial y cualquiera de los vértices de un grafo dado. El algoritmo de Dijkstra presenta una solución por etapas, al estilo de la programación dinámica; cada etapa añade un nuevo vértice al conjunto de vértices, a los que se les conoce su distancia al origen. Cada ruta obtenida se basa en tomar el camino óptimo; si para ir de v_i a v_j es necesario pasar por v_k, los caminos v_i a v_k y v_k a v_j han de ser mínimos.

Algoritmo de Dijkstra en JAVA

Este algoritmo presenta un orden de complejidad de 0(|V|² + |E|), sin utilizar cola de prioridad, o 0(|E| + |V|log|V|), si se utiliza cola de prioridad, y presenta una solución eficiente en cuanto a un camino entre dos nodos.

B. El algoritmo de Floyd

Continuando el trabajo con grafos, otra propuesta algoritmica es presentada cuando se necesita indicar cuál es el camino más corto entre cualquier par de nodos. El algoritmo Floyd, dada la matriz L de adyacencia del grafo g, calcula una matriz D con la longitud del camino mínimo que une cada par de vértices.

Algoritmo de FLOYD en JAVA

La complejidad de este algoritmo es 0(n³). El algoritmo resuelve eficientemente la búsqueda de todos los caminos más cortos entre cualesquiera nodos.

VI. MPLS

LabelSwitching se basa en asociar una pequeña etiqueta de formato fijo con cada paquete de datos para que pueda ser enviado a través de la red. Esto significa que cada paquete, ventana o celda debe tener adicionalmente algún identificador que indica los nodos de la red por los cuales debe pasar.

En cada salto a través de la red, el paquete está enviándose, basado en el valor de la etiqueta de entrada, y reenviado con un nuevo valor de etiqueta. La etiqueta es intercambiada, y los datos son conmutados basados en el valor de la etiqueta, dando lugar a dos términos: "labelswapping" y "labelswitching".

En una red MPLS, los paquetes son etiquetados por la inserción de una pieza adicional de información, llamada shimheader; esto funciona entre la cabecera de red y la cabecera de IP [26].

VII. Dijkstra y GMPLS

El algoritmo de Dijkstra presenta algunas modificaciones, y se han generado sobre él gran cantidad de aplicaciones, dentro de las cuales podemos nombrar las siguientes:

• Encaminamiento de paquetes por los routers.

• Aplicaciones para Sistemas de Información Geográficos.

• Reconocimiento del lenguaje hablado.

• Enrutamiento de aviones, tráfico aéreo.

• Tratamiento de imágenes médicas.

Cada una de estas aplicaciones tiene su razón de ser, por ejemplo, en el encaminamiento de paquetes se da que un mensaje puede tardar cierta cantidad de tiempo en atravesar cada línea; en este caso, tenemos una red con dos nodos especiales, el de inicio y el de llegada. Los pesos de las aristas serían los costes. El objetivo del algoritmo es encontrar un camino entre estos dos nodos cuyo coste total sea el mínimo. Una de las aplicaciones más claras en este tema se da a través de la definición de protocolos como GMPLS[23].

Dentro de las mejores aplicaciones están las que se dan con el uso de soluciones dadas a través de redes neuronales, como la del lenguaje, que tiene dentro de sí mismo múltiples aplicaciones de grafos que en conjunto ayudan a generar un resultado más efectivo [25].

Dentro de los procesos de desarrollo para el ruteo de paquetes también podemos encontrar que otra aplicación se da en la idea de garantizar Calidad del Servicio QoS [24], a través de minimizar el uso de la red y flexibilizar el modelo de reservas.

El MPLS Generalizado, o GMPLS, es una especificación del MPLS que busca eliminar algunos inconvenientes presentados dentro del transporte de información en las redes. Los inconvenientes se presentan en hardware, software o configuración, y se tratan de eliminar por medio de este protocolo [26]. Dentro de la definición de GMPLS encontramos el uso de algunos de los algoritmos ya nombrados, como lo son:

• Bellman-Ford

• Dijkstra

• Dijkstra Modificado

• Bread First Search

• Johnson

• K ShortestPaths

Estos algoritmos son nombrados en otros documentos que muestran su uso, dado que no cumplen exactamente la misma función y no se realizan comparaciones entre ellos; son algoritmos que, en términos generales, realizan la misma tarea, pero cada uno tiene su especialidad [28].

A. Bellman-Ford

Este es un algoritmo que resuelve el problema de, dado un vértice cualquiera, encontrar todos los caminos más cortos a cualquiera de los vértices del grafo. En términos generales, este algoritmo es usado off-line, es decir, es utilizado para realizar un mapa de todas las posibles rutas que se pueden tomar desde un punto a los demás; esto es aplicable a todos los dispositivos de ruteo locales que se utilizan en la red.

B. Dijkstra

Aunque este algoritmo también resuelve el problema de encontrar todos los caminos desde un vértice dado a todos los demás, es muy eficiente encontrando el camino más corto entre una par dado de vértices. Cuando se tiene un paquete de información y se desea construir el camino más corto entre el emisor y el receptor en la red es más económico y rentable utilizar este algoritmo para plantear la ruta.

C. Dijkstra modificado

El algoritmo de Dijkstra presenta algunos fallos para grafos donde algunos arcos tienen pesos negativos. La razón para esto es que dado un vértice removido de la cola de prioridad U no vuelve a ser reetiquetado ni reinsertado dentro de U. En grafos con arcos no negativos esto funciona, sin embargo, cuando se presentan arcos con peso negativo el algoritmo de Dijkstra en su estado original presenta fallas para encontrar los estados o las rutas más cortas, por tal motivo, se hace necesario presentar una alternativa: podría ser cambiar de algoritmo o modificar el algoritmo de Dijkstra reetiquetando los vértices removidos o reinsertándolos en la cola de prioridad. Este algoritmo ha sido planteado de la siguiente manera:

Orden de complejidad: teniendo unas modificaciones sobre el algoritmo de Dijkstra, las cuales se pueden clasificar como insignificantes, dado que solo le agregan procedimientos constantes.

D. BreadthFirstSearch

Dentro de los algoritmos que construyen todos los caminos más cortos desde un punto dado hasta los demás, este algoritmo baja en eficiencia; sin embargo, previene que dentro del proceso no se encuentren ciclos negativos; ya depende del uso de la red y de cómo se necesite el revisar la rentabilidad de su uso.

E. Johnson

Este es un algoritmo muy completo, que permite encontrar todos los caminos más cortos entre cada par de vértices presente en el grafo; es utilizado con el fin de realizar un mapa completo de la red, haciendo evidente el posible uso de segundas rutas más cortas. Es un algoritmo más para uso off-line, es decir, dada su implementación, es más para redes con un cambio mínimo en sus dispositivos conectados.

F. K ShortestPath

No siempre los caminos más cortos son los más efectivos, el K ShortestPath busca los primeros k caminos más cortos entre un par dado de vértices, orientándonos hacia otras posibles rutas, con el fin de obtener rutas más cortas diferentes a la primera, porque sobre esta puede presentarse congestión.

VIII. Modelos y discusiones acerca de la aplicación en GMPLS

Cada uno de los algoritmos tratados en el presente documento presenta una aplicabilidad en diferentes ámbitos; las redes GMPLS tienen heuristicas que se asocian con los algoritmos de grafos y se han planteado a lo largo del documento.

Inicialmente, cada uno de los algoritmos tiene su aplicación dentro del modelo GMPLS; sus aplicabilidades se pueden resumir asi:

• Bellman-Ford: Algoritmo que presenta propiedades interesantes dado que considera las restricciones de enrutamiento, es decir, identifica el camino óptimo entre el origen y el destino a través de máximo h saltos. Es utilizado en RIP, que es la implementación más popular de este tipo de algoritmos [29]. Como es posible notar en la sección VII (A), este algoritmo presenta, en el mejor de los casos, un orden de su número de aristas; sin embargo, también es posible que el orden cambie a un máximo de su número de aristas por su número de vértices, es decir,.

  • for (int k = 1; k < n; k++): Identifica un ciclo con el fin de recorrer y analizar cada uno de los vértices.

  • if (list1 isempty): Identifica una condición que permite bajar el tiempo de ejecución.

  • foreach (edge (v,u): Ciclo que revisa cada uno de los arcos y está anidado en el anterior ciclo nombrado.

De esta manera se identifica el orden de V*E.

• Dijkstra'sAlgorithms: Cada Router GMPLS sirve como la base para el descubrimiento de caminos (cálculos realizados por medio de estos algoritmos), cada nodo de la red realiza esta tarea cada vez que recibe un mensaje a enrutar. La complejidad de estos algoritmos es muy baja cuando se trata de solo calcular el camino más corto entre un par dado de vértices; revisando los algoritmos secciones V(A) y VII(C), el orden para un solo par de vértices es de máximo O(E); el orden se extiende por los ciclos for anidados en el conteo de vértices hasta un máximo de , siendo este el orden para calcular todas las rutas mínimas dadas desde un punto dado a todas las demás ubicaciones.

  • for (int i = 0; i < (distanciasCortas. length - 1); i++): Ciclo que recorre todos los vértices identificando las rutas más cortas de cada uno.

  • for (int j = 0; j <grafo[0].length; j++): Este ciclo está anidado al anterior, recorriendo las posibles rutas más cortas y dando el orden máximo de V*V.

• BreadthFirstSearch: Algoritmo utilizado en el plano de control del GMPLS; tiene como característica especial en este control que dados dos caminos cortos en peso él toma como óptimo el que tiene menor número de arcos [26]; el algoritmo presentado en la sección VII-D muestra un Orden en el cual los ciclos se basan en la cantidad de vértices y una cola de prioridad, presentando un Orden O(n Log |n|).

  • while (Q isnotempty): Ciclo que recorre n vértices en la cola de prioridad.

  • while (u≠null): Este ciclo está anidado al anterior, y con una condición hace que el rango se disminuya en cada acceso que se tiene a él.

  • if (u has notbeenlabeled and edge (w, u): Condición que permite reducir el tiempo de ejecución de forma proporcional a los nodos recorridos.

• K-shortestpath: En los enrutadores de las redes GMPLS se tiene control de la pérdida de información, lo que necesita como opción la selección de caminos que no necesariamente son los más cortos, pero son más seguros y eficientes; el k-shortestpath calcula los primeros k caminos entre dos nodos, con el fin de definir cuál le genera mejor seguridad.

  • Este es un algoritmo al cual no se le define un orden, dado que maneja el uso de otros algoritmos para obtener cada camino más corto.

  • Generalmente es usado el algoritmo de Dijkstra para obtener el camino más corto, y se elimina esta ruta como opción.

  • El algoritmo genera un orden aproximado de k veces O(V*E).

El análisis de cada uno de estos algoritmos se ha realizado con el fin de mostrar los órdenes de complejidad que tiene cada uno y de plantear la discusión de que no se debe elegir entre ellos, dado que cada uno cumple funciones específicas en muchos de los campos de acción, y que es bastante importante la labor que cumple cada uno de ellos dentro del modelo de la red.

A pesar de que en las redes GMPLS se utilizan todos estos algoritmos en su forma original [26], algunos autores prefieren construir nuevos algoritmos que, a nivel de investigación, muestran un mejor resultado; esta construcción la hacen con el fin de mejorar algunas características de las redes [27]. Sin desconocer que los algoritmos aquí nombrados dan solución al problema, lo que hacen es dar solución a casos específicos, añadiendo a ellos fragmentos de código específico.

IX. Conclusiones

La solución de problemas de grafos eficientes para determinadas situaciones genera discusiones, por parte de diferentes autores.

El tema de grafos presenta gran cantidad de algoritmos, y nos permite hacer un mejor análisis de ellos para obtener un estudio de complejidad y determinar de acuerdo con diferentes arquitecturas qué algoritmo se debe usar en las situaciones presentadas.

De acuerdo con cada una de las características de los problemas y con las necesidades, se puede hacer uso de los diferentes algoritmos. Los algoritmos presentes en el actual documento son eficientes en sus respectivos ámbitos.

Si el problema requiere de una solución óptima de camino más corto entre 2 nodos definidos, es posible aplicar Dijkstra o Floyd, sin embargo, es más eficiente Dijkstra, dado que Floyd encuentra todos los caminos más cortos entre cualquier par de nodos.

Otras soluciones de caminos más cortos implican la generación de árboles recubridores que permiten reconstruir cualquier ruta desde un nodo específico. Si este es el requerimiento, es posible utilizar algoritmos de gran eficiencia, como el de Kruskal o el de Prim.

Cuando se habla de algoritmos que ayudan a optimizar la solución de problemas que se pueden representar en forma de grafos, no implica que se tenga que utilizar un solo algoritmo. Los algoritmos presentados en este documento presentan, en su análisis, una eficiencia general muy buena; son los algoritmos mejor clasificados en la solución de problemas de optimización.

La eficiencia de los algoritmos es medible de acuerdo con la utilización de espacio y tiempo que requieren; a través del análisis es posible generar una función matemática que representa su eficiencia; a esto lo debemos llamar análisis de complejidad algoritmica.

Así mismo, es necesario recordar que existe una amplia gama de aplicaciones de estos estudios; algunas de ellas están en el ámbito de las redes de información [18], en las redes de tráfico o en estados de planeación que sirven para cualquier estructura organizacional.

En GMPLS se presenta el uso de algunos algoritmos, incluida la modificación del algoritmo de Dijkstra manteniendo su nivel de complejidad en un orden definido en este algoritmo [29].

Los algoritmos aquí consignados no solo presentan excelente eficiencia, a su vez, en otras comparaciones se hace uso de la mayoría de ellos en forma combinada para mejorar su ejecución y las aplicaciones que pueden tener [28].

El orden de complejidad presentado en este documento para cada uno de los algoritmos obedece a pruebas realizadas sobre JAVA, en las cuales se evidencia que el algoritmo corre de acuerdo con esto, y que también es necesario tener en cuenta los mecanismos de lectura y escritura de la información para evitar aumentar los tiempos de ejecución.

Referencias

[1] A. Duch,"Análisis de Algoritmos", http://www.Isi.upc.edu/duch/home/análisis.pdf, Barcelona, marzo de 2007.

[2] E. Scalise, R. Carmona, "Análisis de Algoritmos y Complejidad", http://ccg.ciens.ucv.ve/~esmitt/ayed/II-2011/ND200105.pdf, Venezuela, ND 2001 05.

[3] T.H.Cormen, C. Stein, R. L.Rivest and C. E. Leiserson, "Introduction to Algorithms", 3^rd. McGraw-Hill Higher Education, 2009.

[4] S. S. Skiena and M. A.Revilla, "Programming challengers", The programming contest training manual, Springer-Verlag, 2003.

[5] H. Zenil, J.-P. Delahaye, "Un método estable para la evaluación de la complejidad algorítmica de cadenas cortas", Computational Complexity (cs. CC); Information Theory (cs,IT), 26 Aug 2011.

[6] J. F. Villalpando B., "Análisis asintótico con aplicación de funciones de Landau como método de comprobación de eficiencia en algoritmos computacionales" e-Gnosis, año/vol 1, 2003, http://www.redalyc.org/articulo.oa?id=73000115.

[7] R.Guerequeta, A. Vallecillo, "Técnicas de diseño de Algoritmos", Universidad de Málaga, Segunda edición, mayo de 2000.

[8] J. A. Manas, "Análisis de algoritmos: Complejidad", http://www.lab.dit.upm.es/~lprg/material/apuntes/o/index.html, noviembre de 1997.

[9] P. F. Gallardo, "Ecuaciones de recurrencia", Capítulo 6, Notas de Matemática Discreta, http://www.uam.es/personal_pdi/ciencias/gallardo/md.htm/.

[10] J. Bermúdez de Andrés, "Diseño de algoritmos", Programación Dinámica, Universidad del País Vasco, 2008.

[11] E. Coto, "Algoritmos Básicos de Grafos", http://www.ciens.unv.ve/~ernesto/nds/CotoND200302.pdf, Venezuela, ND 2003 02.

[12] P. R. Fillottrani, "Algoritmos y Complejidad", Algoritmos sobre grafos, http://www.cs.uns.edu.ar/prf/teaching/AyC09/clase15.pdf, 2009.

[13] H. Araya Carrasco, "Grafos", http://www.ganimides.ucm.lc.

[14] J. Hopcroft, R. Tarjan, "Efficient Algorithms for Graph Manipulation", Cornell University, Ithaca NY, 14850.

[15] J. Sánchez Velásquez, "Introducción al análisis de algoritmos", http://148.201.94.3:8991/F/?func=direct/&local_base=ite01&doc_number=0001116302, México: Trillas, 1998, ct998.

[16] A. Cortés, "Teoría de la complejidad computacional y teoria de la computabilidad", http://sisbib.unmsm.edu.pe/BibVirtualData/publicaciones/risi/N1_2004/a14.pdf, Perú: Lima, 2004.

[17] I. Dora, C. León, C. Rodríguez, G. Rodríguez, A. Rojas, "Complejidad Algorítmica: de la Teoria a la Práctica", http://bioinfo.uib.es/joemiro/aenui/procJenui/Jen2003/docomp.pdf, La Laguna, Tenerife.

[18] M. Amoretti, F. Zanichelli and G. Conte, "Performance evaluation of advanced rouning algorithms for unstructured peer-to-peer networks", Procceding of the 1rt International Conference on Performance Evaluation Methodologies and Tools (valuetools '06), ACM, New York, NY, USA, Article 50.

[19] Y. Yuan, C. Zhiqiang, Z. Hou, M. Tan, "Dynamic programming field based environment learning and path planning for mobile robots", Intelligent Control And Automation (WCICA), IEEE, 2010 8^th World Congress, pp. 883-887, 7-9 July 2010.

[20] P. Marbach, J. N. Tsitsiklis, "A neuro-dynamic programming approach to admission control in ATM networks: the single link case", Acoustics, Speech, and Signal Processing, 1997. ICASSP-97., 1997 IEEE International Conference on, vol.1, no., pp.159-162, 21-24 Apr 1997.

[21] P. K. Singhal, R. N. Sharma, "Dynamic programming approach for solving power generating unit commitment problem", Computer and Communication Technology /IC-CCT), 2011, 2^nd International Conference, pp.298-303, 15-17 Sept. 2011.

[22] T. Hu, T. Wu, J. Song, Q. Liu, B. Zhang,"A New Tree Structure for Weighted Dynamic Programming Based Stereo Algorithm", Image and Graphics (ICIG), 2011 Sixth International Conference, pp.100-105. 12-15 Aug. 2011.

[23] O.J.S. Parra, C. Manta, G. López Rubio, "Dijkstra's Algorithm Model Over MPLS/ GMPLS", Wireless Communications, Networking and Mobile Computing (WiCOM), 2011 7^th International Conference, pp. 1-4, 23-25 Sept., 2011.

[24] S. Tanwir, L. Battestilli, H. Perros and G. Karmous-Edwards, "Dynamic scheduling of network resources whit advance reservations in optical grids", Int. J. Netw. Manag. 18, 2 (March 2008), 79-105, DOI=10.1002/nem.680 http://dx.doi.org/10.1002/new.680.

[25] P. Hegyi, M. Maliosz, A. Ladanyi, T. Cinkler, "Shared protection of virtual private networks, 2003. (DRCN 2003), Proceedings. Fourth International Workshop, pp. 448-454, 19-22 Oct. 2003.

[26] A. Farrel, I. Bryskin, "GMPLS: architecture and applications", San Francisco: Elsevier/Morgan Kaufman, 2006.

[27] A.N.Al-Khwildi, H.S. Al-Raweshidy, "A Proficient Path Selection for Wireless Ad Hoc Routing Protocol", Advanced Communication Technology, 2006, ICACT 2006. The 8^th International Conference, vol.1, pp. 599-604, 20-22 Feb. 2006.

[28] W. Xiao, B.H. Soong, C.L. Law, Y. L. Guan, "Evaluation of heuristic path selection algorithms for multi-constrained QoS routing", Networking, Sensing and control, 2004 IEEE International Conference on, vol.1, pp. 112-116, 21-23 March 2004.

[29] L. N. Binh, "Routing and Wavelength Assignment in GMPLS-based 10 Gb/s Ethernet Long Haul Optical Networks with and without Linear Dispersion Constraints", I.J. Communications, Networks and System Sciences Published (online), http://www.SRPublishing.org/journal/ijcns/, 2008, 2, 105-206.