Artículo

Simulación de la topografía superficial de un cilindrado con corte asistido por vibración

A Cylindrical Surface Topographic Simulation by a Vibration Assisted Cutting Machine

Simulação da topografia superficial de um cilindrado com corte assistido por vibração

Luis Carlos Flórez-García^*; Hernán Alberto González-Rojas^**; Ramón Casado-López^***

* M.Sc. Universidad Tecnológica de Pereira (Pereira-Risaralda, Colombia). luiscflorez@gmail.com
** Ph.D. Universidad Politécnica de Cataluña (Cataluña, España). hernan.gonzalez@upc.edu
*** Universidad Politécnica de Cataluña (Cataluña, España). ramon.casado@upc.edu

Fecha de Recepción: 07 de Marzo de 2014. Fecha de Aprobación: 23 de Mayo de 2014

Resumen

El corte asistido por vibración (CAV) es una técnica de mecanizado que brinda mejor acabado superficial, reduce fuerzas en el corte y aumenta la vida de la herramienta. Para predecir de forma geométrica la topografía de un cilindrado con CAV se ha construido un programa que simula la topografía superficial con el propósito de realizar barridos sobre la frecuencia de vibración, para observar el comportamiento de los parámetros superficiales Sa, St, Ra, Rt y de la topografía. Se ha podido observar que los parámetros superficiales tienen un comportamiento periódico, caracterizado por una frecuencia adimensional igual a 1.

Palabras clave: CAV, Corte asistido por vibración, Corte convencional por torno, Simulador topografía cilindrada.

Abstract

The Vibration Assisted Machining (VAM) is a technique used to provide a better surface finishing, a reduction in the cutting forces, and an increased tool life.To predict a cylinder topographic geometric shape with VAM, there has been built a program, that simulates the surface topography, in order to make sweepings on the frequency vibration, to observe the surface parameters Sa, St, Ra, Rt and the topography'sbehavior. It has been able to observe, that the surface parameters have a periodic behavior, characterized by a dimensionless frequency, equal to 1.

Keywords: VAM, Vibration Assisted Machine, Conventional Lathe Cutting, Cylindrical Topography Simulator, Mechanized Techniques.

Resumo

O corte assistido por vibração (CAV) é uma técnica de mecanizado que oferece um melhor acabado superficial, reduz forças no corte e aumenta a vida da ferramenta. Para prever de forma geométrica a topografia de um cilindrado com CAV se tem construído um programa que simula a topografia superficial com o propósito de realizar varreduras sobre a frequência de vibração, para observar o comportamento dos parâmetros superficiais Sa, St, Ra, Rt e da topografia. Tem-se podido observar que os parâmetros superficiais têm um comportamento periódico, caracterizado por uma frequência adimensional igual a 1.

Palavras chave: CAV, Corte assistido por vibração, Corte convencional por torno, Simulador topografia cilindrada.

I. Introducción

Uno de los métodos para mejorar el corte convencional por torno es el corte asistido por vibración (CAV), pues mejora el acabado superficial, genera mayor precisión en el mecanizado y presenta una alta reducción de la rebaba [1]; además, aumenta la vida de la herramienta de corte para el mecanizado de materiales ferrosos, usualmente de diamante [2], dado que se reducen las fuerzas utilizadas en el corte, debido a que por la vibración de la herramienta disminuye el contacto con el material.

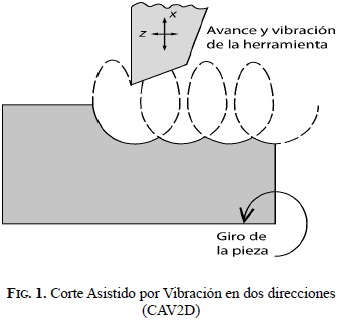
Existen, básicamente, dos métodos de CAV: vibrando en una y en dos direcciones. En una dirección, el movimiento usual es en el eje X del torno (movimiento perpendicular al eje de giro), con o sin la herramienta de corte inclinada. En dos direcciones, el CAV realiza el movimiento tanto en el eje Z (movimiento en la dirección del eje de giro) como en el eje X [3], como se observa en la Figura 1. Estos dos métodos son denominados CAV1D y CAV2D, y corresponden a excitar la herramienta en 1 y 2 ejes, respectivamente. El CAV1D, que usualmente se encuentra en el eje X [4], en algunos estudios se combina con una inclinación en Y e inclusive en Z [5]. En general, el CAV2D muestra mejores resultados que el corte convencional y el CAV1D, al reducir fuerzas en el mecanizado, prolongar la vida de la herramienta y mejorar el acabado superficial [3,6-10].

En este artículo se estudia la topografía superficial dejada por una herramienta de torno utilizando CAV, considerando el problema de corte como un problema de intersección geométrica. Para ello se desarrolló un software que genera la topografía superficial producto del corte, cuando la herramienta está vibrando a cierta frecuencia; con este simulador se pretende buscar las condiciones de corte que mejoren el acabado superficial en un CAV. Para ello, se realizan barridos de frecuencia, con el propósito de investigar la influencia que tiene la frecuencia de vibración en el acabado superficial. Para cada frecuencia se analiza la topografía generada por el simulador, tanto en el eje X como en el eje Z. Producto de este estudio se encuentra una periodicidad del comportamiento de la rugosidad máxima pico valle (Rt) y la rugosidad media (Ra), tanto en la dirección axial Rt_Z y Ra_Z, como en la dirección perimetral del cilindro Rt_Y y Ra_Y. También se evalúa la altura máxima pico valle de una superficie (St) y la rugosidad media sobre una superficie (Sa).

II. Simulador topográfico

Para predecir la topografía superficial en un cilindrado se ha construido un programa en Lazarus v0.9.28.2- Free Pascal, el cual calcula la intersección geométrica de la punta de la herramienta de corte con el material del cilindro a medida que este gira y la herramienta avanza, sin tener en cuenta su espesor. Con esta información se construyen perfiles del corte y se evalúa Ra y Rt, tanto en Z como en X. También se evalúan parámetros del estado superficial, como son Sa y St.

La simulación se realiza dependiendo del caso por analizar; se fija la frecuencia, la amplitud, el desfase y el avance de la vibración en la punta de la herramienta, como se aprecia en las ecuaciones (1) y (2). Se definen los demás parámetros de corte, tales como la velocidad de giro del material, el diámetro de la pieza, el radio de la herramienta, la profundidad de corte y la vibración del material, entre otros.

De acuerdo con la discretización de la punta de la herramienta, fijada en el programa, en un instante se determina la intersección entre la curva de la punta de la herramienta y el material, ignorando el espesor de la herramienta. Repitiendo este procedimiento, a medida que la herramienta avanza en Z y el material gira, se obtiene una topografía superficial característica del corte. Esta topografía superficial es discreta, por lo tanto, el dominio está definido por puntos, que forman una malla que recubre la periferia del cilindro. La imagen de estos puntos representa la topografía superficial resultado del corte.

En la Figura 2 se muestran algunas de las salidas del simulador; por ejemplo, la Figura 2a corresponde a una topografía superficial en coordenadas polares, de una sección transversal cualquiera; en cambio, la Figura 2b corresponde a la misma topografía anterior representada en coordenadas cartesianas. La Figura 2c corresponde a la topografía superficial sobre una sección longitudinal cualquiera.

La condición de corte o datos de entrada para esta simulación se resume en la Tabla 1.

En la Figura 3 se muestra una reconstrucción tridimensional de la topografía superficial para las condiciones antes mencionadas.

III. Resultados

Se muestran los resultados de la simulación topográfica hecha para diferentes condiciones de corte, Figuras 4 y 5; en cada una ellas se evalúan los parámetros de rugosidad Sa, St, Ra_X, Rt_X, Ra_Z y Rt_Z.

La principal característica del CAV es la vibración de la herramienta, por lo tanto, la frecuencia de oscilación es la condición de corte de interés en este estudio. Para evaluar la influencia de esta frecuencia sobre la topografía superficial se realizan barridos entre 1 y 40 kHz.

En general, la topografía superficial producto de la intersección geométrica herramienta-pieza en un CAV depende del valor relativo que existe entre la velocidad de giro de la pieza n y la frecuencia de vibración f. Por ejemplo, si f=kn, con k entero, cada vez que gire la pieza 360º, la posición X de la herramienta respecto al material es la misma; por lo tanto, para el plano XZ múltiplo entero de 360º la herramienta no vibra. Para considerar el efecto del valor relativo entre n y f se introduce una nueva variable que se define como el cociente f entre n, luego, los parámetros del estado superficial Ra, Rt, Sa y St serán graficados en función de esta nueva variable adimensional, f/n.

En la Figura 4 se muestra la gráfica de Sa, St, Ra_X, Rt_X, Ra_Z y Rt_Z simulados, para un CAV en el que la herramienta vibra tanto en el eje X como en el eje Z, para el intervalo de vibración mostrado en la Tabla 2, que resume las condiciones de corte de este experimento.

En la Figura 4a se observa un comportamiento mínimo local para Rt_Z está desfasado en 0,5 respecto a periódico caracterizado por unos valles con período Rt_X; por lo tanto, no es posible encontrar una condición adimensional 1, tanto para Rt_Z, Rt_X y St. Así como el que minimice simultáneamente a Rt_Z y Rt_X. mínimo y máximo local para Rt_X y St coinciden, el mínimo local para Rt_Z está desfasado en 0,5 respecto a Rt_X; por lo tanto, no es posible encontrar una condición que minimice simultáneamente a Rt_Z y Rt_X.

En la Figura 4b se observa una situación similar a la mostrada en 4a; los mínimos locales tienen un período igual a uno, y el mínimo local para Ra_Z está desfasado en 0,5 respecto a Ra_X. A diferencia con la gráfica anterior, el mínimo local para Ra_X corresponde a un pico máximo de Ra_Z.

De las Figuras 4a y 4b se puede deducir que el mínimo local tanto para Rt_Z como Ra_Z se producen para el mismo f/n. Una situación similar ocurre para St y Sa, solo que este mínimo está desfasado con respecto a la posición del mínimo de Rt_Z y Ra_Z; lo que en un caso es un mínimo, en el otro es un máximo; por lo tanto, el mínimo para los parámetros de estado superficiales Sa y St no coinciden con el mínimo para los parámetros de estado sobre una línea Ra y Rt.

En la Figura 5 se puede ver un detalle de la curva Rt_Z; en ella se destacan 4 puntos de interés, los parámetros de rugosidad, la frecuencia de vibración y la velocidad de giro de la pieza; estos 4 puntos se encuentran resumidos en la Tabla 3.

En las Figuras 2, 3, 6, 7 y 8 se muestran las topografías superficiales 2D y 3D asociadas a los 4 puntos antes mencionados. En las Figuras 2b y 2c se observa la simulación de CAV del punto 1; en ella se puede ver la forma que adquiere la topografía longitudinal (Figura 2c), definida por la punta de la herramienta, la cual se imprime en el cuerpo por cilindrar, corte tras corte, de forma ordenada, a medida que gira el cuerpo y avanza la herramienta con un movimiento senoidal. La sección transversal (Figura 2a) muestra el error de cilindricidad, que se define como la diferencia entre el diámetro máximo y el mínimo de la envolvente de la señal oscilatoria. En la Figura 3 se aprecia la topografía superficial caracterizada por 8 picos. En un corte XZ se ve el arco de circunferencia definido por la punta de la herramienta.

En la Figura 6 se muestra la topografía superficial para una relación f/n que minimiza la Rt_Z, punto 2. El comportamiento de la rugosidad transversal (Figura 6a) es idéntico al comportamiento mostrado en la Fig. 2b, lo que era de esperar, ya que el parámetro RtX no experimenta grandes cambios en este intervalo (ver Figura 4a). En cambio, la Figura 6b es muy diferente a la Figura 2c; en la primera se encuentra la forma de la punta de la herramienta impresa en el material, una tras otra de forma ordenada, sin la oscilación senoidal; por lo tanto, cada vez que la pieza gire una vuelta completa, la herramienta se encuentra en la misma posición instantánea que tenía en la vuelta anterior, lo que llamaremos sincronismo Rt_Z entre el giro de la pieza y la vibración de la herramienta. La rugosidad máxima pico valle Rt_Z, cuando hay sincronismo en Rt_Z, es de 3.18 μm, valor que se mantiene en todos los cortes longitudinales de este mecanizado. Dependiendo de dónde se realice el corte del plano XZ, la altura mínima del perfil variaría según la forma definida por la Figura 6a, por lo tanto, la posición mínima del corte longitudinal estará entre -2 y1,9 μm. Debido a lo anterior, la topografía superficial (Figura 6c) tiene a lo largo del eje Z picos de la misma altura. Esta topografía es similar a la del punto 1 (Figura 3), debido a los rangos de la gráfica.

Con referencia al punto 3 de la Figura 5, se destaca como la condición que produce el menor valor de St (ver Tabla 3). La topografía perimetral (Figura 7a) difiere de las topografías perimetrales mostradas en las Figuras 1b y 5a. En la Figura 7a se puede ver que no existe un pico de rugosidad máxima, sino una región comprendida entre 20 mm y 40 mm, donde se encuentran los máximos para Rt_X. Por otra parte, en la Figura 7b se puede ver cómo la punta de la herramienta oscila en la dirección X, afectada por una amplitud de oscilación más pequeña que la oscilación que afecta la topografía superficial de la Figura 2c. También se puede ver cómo en la Figura 7c aparecen más picos que en la Figura 3, modificándose con ello la topografía superficial. Además, se puede comprobar que la distancia máxima pico valle St, para el dominio mostrado en la Figura 7c, es menor que la distancia máxima pico valle St de la Figura 3.

El punto 4 presenta características de rugosidad muy similares a las del punto 3, de acuerdo con la Tabla 3. Debido a lo anterior, las características del corte transversal (Figura 8a) son similares a las del punto 3. Al contrario de la sección longitudinal del punto 3, en la sección longitudinal del punto 4 (Figura 8b) se presenta un comportamiento oscilatorio periódico donde la herramienta penetra poco, luego mucho y así sucesivamente. Cada pico tiene la misma altura, y cada dos valles se encuentra el punto más bajo, consecuentemente, el Ra del punto 4 es mayor que el del punto 3. La representación topográfica de este mecanizado (Figura 8c) es muy similar a la del punto 3, donde los picos tienen una altura menor a las topografías de los puntos 1 y 2.

IV. Conclusiones

La sección transversal, para todos los cortes, muestra un comportamiento repetitivo en cuanto a su forma, representando el costado de un canal dejado por la herramienta, como el canal de una rosca de tornillo. A pesar de las mejoras obtenidas por el CAV, se puede observar la dificultad de llegar a esta configuración de corte debido a las pequeñas diferencias en f/n.

Las características de rugosidad más bajas se presentan en el punto 3, a excepción de las del corte longitudinal del punto 2. Si se busca en un corte precisión y redondez de la pieza, se debe utilizar un corte con características similares a las del punto 3.

La siguiente conclusión es de un análisis de CAV desde el punto de vista geométrico: Existe un comportamiento periódico de los parámetros de estado superficial, caracterizado por una frecuencia adimensional f/n igual a 1.

IV. Referencias

[1] C. Ma, E. Shamoto, T. Moriwaki, Y. Zhang, L. Wang, "Suppression of burrs in turning with ultrasonic elliptical vibration cutting", International Journal of Machine Tools & Manufacture, 45, pp. 1295-1300, 2005.

[2] E. Shamoto, T. Moriwaki, "Ultaprecision Diamond Cutting of Hardened Steel by Applying Elliptical Vibration Cutting", Annals of the ClRP, Vol. 48, pp. 371-375, 1999.

[3] D. E. Brehl, T. A. Dow, "Review of vibrationassisted machining", Precision Engineering 32, pp. 153-172, 2008.

[4] M. Xiao, K. Sato, S. Karube, T. Soutome, "The effect of tool nose radius in ultrasonic vibration cutting of hard metal", International Journal of Machine Tools & Manufacture 43, pp. 13751382, 2003.

[5] M. Jin, M. Murakawa, "Development of a practical ultrasonic vibration cutting tool system", Journal of Materials Processing Technology 113, pp. 342-347, 2001.

[6] C. Ma, E. Shamoto, T. Moriwaki, Y. Zhang, L. Wang, "Suppression of burrs in turning with ultrasonic elliptical vibration cutting", International Journal of Machine Tools & Manufacture 45, pp. 1295-1300, 2005.

[7] C. Nath, M. Rahman, "Effect of machining parameters in ultrasonic vibration cutting", International Journal of Machine Tools & Manufacture, Vol. 48, pp. 965-974, 2008.

[8] C. Ma, E. Shamoto, T. Moriwaki, L. Wang, "Study of machining accuracy in ultrasonic elliptical vibration cutting", International Journal of Machine Tools & Manufacture, Vol. 44, pp. 1305-1310, 2004.

[9] C. Nath, M. Rahman, K. S. Neo, "Machinability study of tungsten carbide using PCD toolsunder ultrasonic elliptical vibration cutting", International Journal of Machine Tools & Manufacture (Artículo Aceptado), 2009.

[10] C. Nath, M. Rahman, K. S. Neo, "A study on ultrasonic elliptical vibration cutting of tungsten carbide", Journal of Materials Processing Technology, Vol. 209, pp. 4459-4464, 2009.

[11] A. S. Adnan, S. Subbiah, "Experimental investigation of transverse vibration-assisted orthogonal cutting of AL-2024", International Journal of Machine Tools and Manufacture, Volume 50, Issue 3, March 2010, pp. 294-302.

[12] X. Zhang, M. Arif, K. Liu, A. S. Kumar, M. Rahman,"A model to predict the critical undeformed chip thickness in vibration-assisted machining of brittle materials", International Journal of Machine Tools and Manufacture, Volume 69, June 2013, pp. 57-66.