Modelación y simulación de un pervaporador acoplado a un proceso de sacarificación-fermentación para la producción de etanol
Modeling and simulation of a pervaporator coupled to a simultaneous saccharification-fermentation process for the ethanol production
Modelação e simulação de um pervaporador acoplado a um processo de sacarificação-fermentação para a produção de etanol
Jairo Antonio Cubillos-Lobo*, Felipe Bustamante-Londoño**, Alejandro Acosta-Cárdenas***
* Ph. D. Universidad Pedagógica y Tecnológica de Colombia (Tunja-Boyacá, Colombia). jairo.cubillos@uptc.edu.co.
** Ph. D. Universidad de Antioquia (Medellín-Antioquia, Colombia). fbustama@udea.edu.co.
*** M. Sc. Universidad de Antioquia (Medellín-Antioquia, Colombia). alejandro.acosta@udea.edu.co.
Cómo citar este artículo: [1] J. A. Cubillos-Lobo, F. Bustamante-Londoño & A. Acosta-Cárdenas, "Modelación y simulación de un pervaporador acoplado a un proceso de sacarificación-fermentación para la producción de etanol", Fac. Ing., vol. 24 (40), pp. 49-66, Sep.-Dic. 2015.
Fecha Recepción: 30 de junio de 2015 Fecha Aprobación: 18 de agosto de 2015
Resumen
Actualmente, la integración de procesos es considerada una opción viable para reducir costos en la producción de etanol a partir de biomasa. Simulaciones y resultados experimentales han demostrado los beneficios de la integración de las etapas de sacarificación y fermentación y del acoplamiento del proceso de fermentación a la recuperación in-situ de etanol por pervaporación en la producción de bioetanol; sin embargo, no se han publicado estudios de la integración del proceso de sacarificación-fermentación simultánea con membranas de separación, para la remoción insitu de etanol a partir del caldo de fermentación. En este trabajo se aborda esta necesidad, mediante la modelación y simulación de la producción de etanol a partir de almidón de yuca por sacarificación-fermentación simultánea, acopladas a un sistema de remoción in-situ de etanol por pervaporación, con membranas a base de polidimetilsiloxano (PDMS), silicalita y PDMS-Silicalita. La membrana de PDMS se modeló usando el mecanismo de solución-difusión, mientras que para la membrana de silicalita se utilizó el modelo de adsorción-difusión. Para el modelo del proceso de sacarificaciónfermentación simultánea (SSF) se utilizó una fusión del modelo multicadena (Michaelis-Menten), junto con un modelo tipo Monod. El ajuste del modelo de SSF a los datos experimentales reportados, así como de los modelos de membranas de PDMS y silicalita a los valores reportados en la literatura es bueno: la máxima desviación encontrada es del orden de 3%. El modelo integrado se utilizó para predecir la concentración de etanol en función del tiempo durante la sacarificación-fermentación simultánea.
Palabras clave: Sacarificación-fermentación simultánea, Bioetanol, Pervaporación, PDMS, Silicalita, Modelación y simulación, Integración de procesos.
Abstract
Process integration is now days considered a viable option for reducing ethanol production costs from biomass. Both experimental and simulation results have shown the benefits of coupling saccharification and fermentation as well as fermentation and pervaporation. However, the integration of simultaneous saccharification-fermentation with membrane-based in-situ removal of ethanol, which would allow reaching the benefits of this approach, has not been reported yet. This work aims to obtain the modelling and simulation’s results in the production of ethanol, from cassava starch by simultaneous saccharification and fermentation, coupled with the membranes separation, based on Silicalite PDMS, and PDMS-Silicalite.
A combined solution-diffusion mechanism and adsorption-diffusion mechanism was used for modelling the PDMS membrane where as the Maxwell-Stefan multi-component mass-transfer equations were used for modelling the silicalite membrane..A simultaneous-saccharification and fermentation process was modelled, using a multi-chain model (Michaelis-Menten) coupled with the Monod model. The maximum deviation found in the adjusted SSF model to the reported experimental data, as well as the values for PDMS and silicalite membrane models, is in the 3% range. The integrated model was used to predict the ethanol concentration during the simultaneous saccharification-fermentation process.
Keywords: Simultaneous Saccharification Fermentation, Bioethanol, Pervaporation, PDMS, Silicalite, Modelling and Simulation, Process integration.
Resumo
Atualmente, a integração de processos é considerada uma opção viável para reduzir custos na produção de etanol a partir de biomassa. Simulações e resultados experimentais têm demonstrado os benefícios da integração das etapas de sacarificação e fermentação e do acoplamento do processo de fermentação à recuperação in situ de etanol por pervaporação na produção de bioetanol; porém, não tem sido publicados estudos da integração do processo de sacarificação-fermentação simultânea com membranas de separação, para a remoção in situ de etanol a partir do caldo de fermentação. Neste trabalho se aborda esta necessidade, mediante a modelação e simulação da produção de etanol a partir de amido de mandioca por sacarificação-fermentação simultânea, acopladas a um sistema de remoção in situ de etanol por pervaporação, com membranas a base de polidimetilsiloxano (PDMS), silicalita e PDMS-Silicalita. A membrana de PDMS modelou-se usando o mecanismo de solução-difusão, enquanto que para a membrana de silicalita se utilizou o modelo de adsorção-difusão. Para o modelo do processo de sacarificação-fermentação simultânea (SSF) utilizou-se uma fusão do modelo de várias correntes (Michaelis-Menten), junto com um modelo tipo Monod. O ajuste do modelo de SSF aos dados experimentais reportados, assim como dos modelos de membranas de PDMS e silicalita aos valores reportados na literatura é bom: o máximo desvio encontrado é da ordem de 3%. O modelo integrado utilizouse para predizer a concentração de etanol em função do tempo durante a sacarificação-fermentação simultânea.
Palavras chave: Sacarificação-fermentação simultânea, Bioetanol, Pervaporação, PDMS, Silicalita, Modelação e simulação, Integração de processos.
I. Introducción
Actualmente, el biocombustible más importante es el etanol, producto completamente renovable obtenido a partir de cultivos bioenergéticos y biomasa. El etanol es utilizado como aditivo oxigenante de la gasolina, con el fin de reducir las emisiones de monóxido de carbono, compuestos aromáticos y compuestos orgánicos volátiles [1]. Tradicionalmente, la producción de etanol a partir de almidón se lleva a cabo por la sacarificación de este polisacárido para convertirlo en azúcares fermentables, que son transformados en alcohol mediante levaduras [2, 3]; sin embargo, la concentración de alcohol producido oscila alrededor del 10% p/p, lo cual hace necesario un costoso proceso adicional de purificación para alcanzar la concentración requerida (>99% p/p) para mezclarlo con gasolina en proporciones del 10 al 20% p/p [4]; por tanto, el costo de producción de etanol anhidro es elevado y poco competitivo frente a los combustibles fósiles convencionales; pero la integración de procesos, por ejemplo, mediante la sacarificación-fermentación simultánea (SSF, por sus siglas en inglés), podría mejorar en forma significativa la productividad del proceso [5].
La SSF presenta la ventaja de simplificar el proceso, reduce el número de reactores necesarios, los tiempos de proceso, las demandas de energía y los costos de producción [6]; sin embargo, en este proceso se presenta inhibición del metabolismo de los microorganismos encargados de la fermentación; esto ocurre a una concentración de etanol del orden de 10% p/p, lo que se traduce en una disminución de la actividad microbiana y, por ende, en el rendimiento del etanol [7]. Como solución a este problema se han planteado diferentes alternativas para la remoción in situ del etanol del medio fermentativo, de forma que la concentración de etanol se mantenga por debajo del valor inhibitorio; entre estas técnicas de remoción de etanol se destaca la pervaporación, proceso de separación de membranas que ha adquirido cada vez mayor interés, pues es eficiente desde el punto de vista energético, en comparación con tecnologías convencionales como la destilación y la adsorción [8].
En la pervaporación se pone una mezcla líquida en contacto con la superficie de una membrana, buscando que el compuesto que se va a separar se transporte preferentemente a través de ella; el lado de la membrana en contacto con la solución de trabajo se conoce como "retenido" o "alimento", y el otro lado, como "permeado"; sin embargo, pese a las múltiples ventajas económicas y técnicas que presenta este nuevo proceso de producción de alcohol, los fenómenos enzimáticos y de transporte de materia asociados son complejos; por esta razón, la modelación y simulación fundamentada en principios termodinámicos y cinéticos constituye una herramienta muy poderosa para determinar si el funcionamiento de este proceso es viable a nivel industrial; además, esta herramienta tiene otras ventajas, como encontrar las mejores condiciones de proceso, reduciendo así el trabajo experimental y mejorando los índices de desempeño ambiental. Por tanto, en este artículo se reporta la modelación y simulación de la sacarificación-fermentación simultánea de almidón acoplada a un pervaporador, empleando una aproximación fenomenológica; la solución de los modelos y su simulación se realiza con MatLab.
II. Metodología
A. Modelo de la sacarificación-fermentación simultánea (SSF)
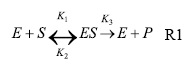
La primera etapa del proceso es la sacarificación, donde se lleva a cabo la hidrólisis enzimática del almidón para la producción de la glucosa, que, posteriormente, pasa a la etapa de fermentación, donde se produce el etanol. Se han sugerido diferentes modelos para esta etapa, los cuales, generalmente, se basan en ecuaciones cinéticas del tipo Michaelis-Menten, en el mecanismo multicadena y en la ecuación de Briggs-Haldane [9]. En este trabajo se utilizó el mecanismo multicadena, que se fundamenta en la ecuación de Michaelis-Menten o de equilibrio rápido estacionario, donde la transformación enzimática de sustrato (S) a producto (P) transcurre a través de la formación de un complejo enzimasustrato (ES), en equilibrio con la enzima (E) y el sustrato (S), que se descompone dando origen a los productos de reacción (P), Reacción 1.
En la etapa de sacarificación se utiliza igualmente un modelo basado en el mecanismo multicadena [10], donde se considera que el almidón se hidroliza completamente con α-amilasa. Por tanto, el grado promedio de polimerización (DP, por sus siglas en inglés) es 5, y es imposible alcanzar la completa conversión del almidón a glucosa [10]. Así mismo, se considera que los oligosacáridos están formados por dos fracciones: una susceptible a la hidrólisis, que comprende el 77% de las moléculas (enlaces α-1,4), y otra que contiene enlaces α-1,6 que son resistentes a la hidrólisis [10]. El balance de masa para la fracción de almidón susceptible y resistente a la hidrólisis puede expresarse en forma diferencial, como se indica en las Ecuaciones (1) y (2) [11, 12] (en la Tabla 1 se muestra la definición de variables del modelo):
Por tanto, la velocidad total de degradación del almidón es (3):
Donde:
La concentración de las enzimas (Enz) depende de la velocidad de síntesis de enzimas (Renz), de la velocidad de dilución del medio debido al crecimiento de la biomasa y de la velocidad de degradación de las enzimas (β), Ecuación (6) [13,14]:
Donde:
La velocidad de crecimiento de la biomasa se obtiene a partir del modelo de la etapa de la fermentación, en la cual se lleva a cabo la conversión de la glucosa y de los azúcares reductores, provenientes de la hidrólisis del almidón en etanol. Se han publicado diversos modelos de la fermentación de glucosa, los cuales generalmente se basan en ecuaciones tipo Monod, aproximación que también se usa en este trabajo. En concreto, el crecimiento del microorganismo que realiza la fermentación (Saccharomyces cerevisiae) puede expresarse como (8) [15]:
Donde,
B. Modelo del proceso de pervaporación
1) Modelado de las membranas de PDMS
En primera instancia se modeló el transporte de etanol a través de membranas PDMS en estado estacionario. El modelo fenomenológico empleado fue el modelo de solución-difusión. Luego se incluyó la variación temporal de la concentración de etanol que se presenta durante la fermentación; este cambio en la concentración de etanol está determinado por la velocidad de producción de etanol en el proceso de la sacarificación-fermentación simultánea (SSF) y la velocidad de permeación del etanol a través de la membrana. Las consideraciones del modelo son las siguientes:
El desarrollo del modelo en estado no estacionario para la membrana PDMS se resume a continuación (referirse en la Tabla 1 para la definición de variables del modelo). Partiendo de la ecuación de Fick se tiene que el flux másico del etanol (jA(t) a través de la membrana es directamente proporcional al coeficiente de difusión en la membrana e inversamente proporcional a su espesor (10):
Considerando que, por definición,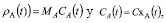 
, se tiene (11):
La fracción molar de etanol en la superficie superior de la membrana (xA0(m)) puede relacionarse con su concentración en el fermentador ) mediante(xA0un balance de masa en la interfase superior de la membrana. De igual forma, la fracción molar de etanol en la superficie inferior (xAe(m)) puede relacionarse con su concentración en el permeado (xAe mediante un balance de masa en la interfase inferior de la membrana. Además, puesto que en el proceso se llega a un equilibrio líquido-vapor, deben involucrarse los coeficientes de actividad (γA). El resultado final se muestra en (12); los detalles de la derivación se presentan como material complementario al artículo.
Donde PA representa la permeabilidad del etanol en la membrana, la cual depende de su solubilidad (SAm) y coeficiente de difusión (DAm) en la membrana (13):
La difusividad del etanol en la membrana puede ser expresada por la teoría del transporte de volumen libre [16] como (14):
Utilizando la ecuación del virial truncada hasta el segundo término y el modelo de UNIQUAC para evaluar los coeficientes de fugacidad y de actividad, (15) y (16), respectivamente, del etanol se tiene:
Introduciendo la definición de selectividad (α), Ecuación 17, el flux de etanol a través de la membrana está dado por (18).
2) Modelado de las membranas de silicalita
Por tratarse de un material microporoso, se empleó el modelo de adsorción-difusión, que considera la adsorción de los componentes de una mezcla en la superficie de la membrana, y su posterior difusión a través de esta gracias a un gradiente de potencial químico, seguida por la desorción en forma de vapor de los compuestos que permearon (Fig. 1). La difusión dentro de la membrana se basa en las ecuaciones de Maxwell-Stefan [17].
Las simplificaciones implementadas en el desarrollo del modelo son las siguientes:
En las ecuaciones de difusión multicomponente de Maxwell-Stefan se tienen en cuenta las interacciones entre la difusión de los diferentes componentes de la mezcla, como se muestra en (19):
Es importante destacar que debido a que la concentración de etanol en la superficie de la membrana varía con el tiempo, la fracción de sitios ocupados y la difusividad superficial también son dependientes del tiempo. La fracción de sitios ocupados se define como:
Ahora, el flux para la especie i a través de la membrana de la zeolita se puede definir en función de su velocidad:
Reemplazando (21) en (19) y reordenando términos para el sistema binario etanol-agua y teniendo en cuenta que para membranas de zeolita que muestran una alta selectividad, como es el caso de la silicalita, se considera que principalmente un componente permea a través de la membrana, se tiene:
Donde la especie 1 es el etanol.
Suponiendo que la difusión acoplada de las especies (Ds12) tiende a infinito,(29) se convierte en:
El gradiente de potencial químico (∇μ1) puede ser representado como el gradiente de la ocupación del sitio de cada especie [18]:
Donde la actividad (a) depende de la fracción de sitios ocupados y, por tanto, es función del tiempo. Igualando (23) y (24) se obtiene:
La ecuación 25 describe el flux en función del tiempo de cada uno de los componentes a través de los poros de la zeolita. La naturaleza de las funciones (∂ lna1(t)/∂ θ1(t)) y (∂ lna1(t)/∂ θ2(t))dependerá de la naturaleza de la isoterma de adsorción del etanol en la zeolita. La difusividad Ds 1v(t) también es dependiente de la fracción de los sitios ocupados. Por tanto, para modelar el flujo de cada uno de los componentes a través de la zeolita deben conocerse las características de difusión y adsorción. En este sentido, debido al estrecho diámetro de poro de la silicalita puede suponerse que solamente una molécula se difunde a la vez. Por tanto, la difusividad de Maxwell-Stefan Ds 1v(t)depende linealmente de los sitios vacantes (θV), (26) y (27) [19]:
Por otro lado, la difusividad a dilución infinita depende de la temperatura, de acuerdo con la ecuación de Arrhenius (28) [20]:
Asumiendo que la adsorción del etanol se puede describir con la isoterma de adsorción de Langmuir, la actividad (a1(t)) en la zeolita para una determinada fracción de ocupación del sitio (θ1(t)) está dada por (29):
Donde la constante de Langmuir (s) es función de la temperatura.
Finalmente, el flux de etanol a través de la membrana está dado por (30):
Modelo de la membrana compuesta PDMS + silicalita
También se modelaron membranas compuestas PDMS y Silicalita. Un primer caso es cuando una capa de PDMS se deposita sobre una capa de silicalita (la película de PDMS está en la parte superior debido a su mayor resistencia al envenenamiento por los subproductos de la fermentación); en este caso puede emplearse un modelo de resistencias en serie, como se ilustra en la Fig. 2. En este modelo, el fluxa través de la capa de PDMS es el mismo que a través de la silicalita, pudiendo igualarse (18) y (30) para calcular la concentración del etanol en la interface de las capas y a la salida de la membrana compuesta (concentración de permeado).
III. Resultados y discusión
A. Simulación del modelo sacarificación fermentación simultánea
El modelo de la SSF se implementó en MatLab. Los resultados del modelo se compararon con los obtenidos por el Grupo de Biotransformación, de la Universidad de Antioquia, para la producción de etanol a partir de almidón de yuca; las condiciones bajo las cuales se realizaron los experimentos son: biorreactor de 5 L, enzima AMG y Termamil, levadura ETHANOL RED, temperatura: 36°C, pH: 4.5.
El ajuste del modelo a los resultados experimentales es muy bueno (Fig. 4 a 6); en efecto, la desviación máxima encontrada entre los valores experimentales y simulados es del 3%. Puesto que lo más importante del modelo acoplado es determinar la concentración de etanol en función del tiempo, a continuación se muestra el efecto de diferentes parámetros de operación sobre el desempeño del sistema:
B. Simulación del modelo de pervaporación
1) Simulación del modelo de las membranas de PDMS y silicalita
Los modelos de solución-difusión y adsorción difusión arrojaron un buen ajuste a los datos experimentales reportados para la separación de etanol con membranas de PDMS y silicalita [20- 27], respectivamente (ver Fig. 6). Las condiciones experimentales empleadas en cada referencia se indican en la Tabla 2; estas condiciones se usaron como parámetros de entrada en la simulación.
2) Simulación del modelo de las membranas compuestas de PDMS-Silicalita compuestas de PDMS-Silicalita importante destacar que en el modelo se tomaron los datos experimentales de concentración de etanol
Inicialmente, el modelo por capas se validó con los resultados reportados por diferentes autores. Los resultados se muestran en la Fig. 7, donde las líneas continuas son las predicciones del modelo, y los puntos son los valores experimentales reportados [28-30]; las condiciones experimentales empleadas en cada referencia se indican en la Tabla 3. Es importante destacar que en el modelo se tomaron los datos experimentales de concentración de etanol en función del tiempo reportados por cada autor; es decir, no se utilizó el modelo de sacarificación fermentación simultáneas. En todos los casos se encontró una diferencia menor al 2% entre los datos calculados con el modelo y los reportados en la literatura.
Con el modelo validado se estudió el efecto de diferentes condiciones de operación (temperatura del alimento, presión de vacío, espesor de la membrana de PDMS y silicalita) sobre el desempeño de la separación de etanol en mezclas modelo etanolagua. A continuación se reseñan las principales observaciones encontradas:
C. Simulación del modelo del proceso sacarificaciónfermentación simultánea acoplado al pervaporador
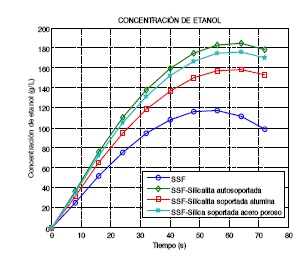
La Fig. 8 muestra los resultados de la simulación de la SSF acoplada a membranas de PDMS y silicalita preparadas sobre diferentes soportes (autosoportadas -este es un caso ideal, pues debido al pequeño espesor de la membrana es necesario tener un soporte-; material polimérico-politetrafluoroetileno-, y acero poroso). El eje y de ambas gráficas representa la concentración de etanol en el permeado a un tiempo dado, mientras que la línea base (curva "SSF") indica la concentración esperada dentro del biorreactor a ese mismo tiempo.
El efecto de la membrana de silicalita sobre la SSF es mucho más significativo que el efecto de la membrana de PDMS, lo cual se explica por su mayor flux; sin embargo, en ambos casos se obtiene un considerable incremento de la concentración de etanol recuperado cuando el proceso se acopla a las membranas. Además, debe notarse que el tiempo para alcanzar la concentración máxima de etanol se retrasa cerca de 15 horas con respecto al proceso sin separación de etanol. De la misma manera, la incorporación de las membranas aumenta la velocidad de producción de etanol, tal como se puede concluir a partir de la pendiente de las curvas de la Figura 8; todo esto apunta a una mejora en la productividad del proceso global. Como ya se ha dicho, la silicalita, pese a su mejor desempeño, no es un candidato viable para el sistema SSF+membrana, puesto que presenta mayor susceptibilidad al envenenamiento con los subproductos de la fermentación; por esta razón, se ha explorado la preparación de membranas compuestas PDMS-Silicalita, cuya matriz polimérica mejore la durabilidad de la membrana en las condiciones presentes en el biorreactor.
La Fig. 9 compara el desempeño de las membranas compuestas PDMS-Silicalita, por capas (PC) y mezclada (MX). El comportamiento de las membranas mezcladas es intermedio al de las membranas de silicalita y PDMS; además, puede observarse que la membrana compuesta (con una carga del 50% de silicalita) presenta mejor desempeño.
IV. Conclusiones
Los modelos fenomenológicos desarrollados permiten simular adecuadamente el proceso de sacarificación fermentación simultánea, la recuperación de etanol por pervaporación y el proceso acoplado, y estudiar el desempeño del sistema bajo diferentes condiciones de operación. Además, el uso de una membrana compuesta por capas de PDMS+Silicalita es una opción viable para la remoción in-situ de etanol desde el caldo de fermentación; en efecto, esta configuración tiene mayor resistencia al envenenamiento por los subproductos del caldo de fermentación que las membranas de silicalita.
V. Agradecimientos
A la Dirección de Investigaciones (DIN) de la Universidad Pedagógica y Tecnológica de Colombia, por la financiación de este trabajo a través del proyecto SGI 1571.
Referencias
[1] http://www.biocombustibles.es, Consultada junio 2015.
[2] R. Wooley et al., "Process design and costing of bioethanol technology: a tool for determining the status and direction of research and development". Biotechnol. Prog Vol. 15, pp. 794-803, 1999.
[3] J. Mielenz, "Ethanol production from biomass: technology and commercialization status". Current Opinion in Microbiology. Vol. 4, pp. 324-329. 2001.
[4] C. Wyman, "Ethanol from lignocellulosic biomass: Technology, economics, and opportunities". Bioresource Technol. Vol. 50, pp. 3-16, 1994.
[5] H. Castaño and C. E. Mejía. "Producción de etanol a partir de almidón de yuca utilizando la estrategia de proceso sacarificación fermentación simultáneas (SSF)", Vitae, Vol. 15, pp. 251-258, 2008.
[6] C. A. Cardona and Ó. J. Sánchez. "Fuel ethanol production: Process design trends and integration opportunities", Bioresource Technology, Vol. 98, pp. 2415-2457, 2007.
[7] K. Wasewr and V. Pangarkar. "Intensification of Recovery of Ethanol from Fermentation Broth Using Pervaporation: Economic Evaluation". Chemical and Biochemical Engineering Quarterly. Vol. 20, pp. 135-145. 2006.
[8] F. Lipnitzki and R. Field, "Pervaporation-based hybrid process: a review of process design, application and economics", J. Membr. Sci. Vol. 153, pp. 183-210. 1999.
[9] E. Nagy, B. Bakó and L. Szabó, "A kinetic study of the hydrolysis of maltodextrin by soluble glucoamylase". Starch/starke. Vol. 4, pp.145-149, 1992.
[10] G. Zanin and F. Moraes, "Modelling cassava starch saccharification with amyloglucosidase", Applied Biochemistry and Biotechnology.Vol. 57/58, pp. 617-625, 1996.
[11] A. Kroumov, A. Modenes and M. Tait, "Development of new unstructured model for simultaneous saccharification and fermentation of starch to ethanol by recombinant strain". Biochemical Engineering Journal. Vol. 28, pp. 243-255, 2006.
[12] M. Matsamura and J. Hirata, "Continuous Simultaneous Saccharification and Fermentation of Raw Starch in a Membrane Reactor", J. Chem. Tech. Biotechnol. Vol. 46, pp. 313-326, 1989.
[13] C. South, A. Hogsett and L. Lynd, "Modeling simultaneous saccharification and fermentation of lignocelluloses to ethanol in batch and continuous reactors", Enzyme and Microbial Technology.Vol. 17, pp.797-803, 1995.
[14] K. Olofsson, A. Rudolf and G. Liden, "Designing simultaneous saccharification and fermentation for improved xylose conversion by a recombinant strain of Saccharomyces cerevisiae", Journal of Biotechnology.Vol. 134, pp.112-120, 2008.
[15] S. Ochoa, A. Yoo, J. Repke, G. Wozny and D. Yang, "Modeling and Parameter Identification of the Simultaneous Saccharification-Fermentation Process for Ethanol Production", Biotechnol.Prog. Vol. 23, pp.1454-1462, 2007.
[16] J. S. Vrentasand and J. L. Duda, "Diffusion in Polymer-Solvent Systems. Reexamination of the Free-Volume Theory", J. Polymer Sci., Polymer Phys. Ed. Vol. 15, pp. 403, 1977.
[17] D. Schuring, Diffusion in Zeolites: Towards a Microscopic Understanding. Data Library Technische Uni-versiteit Eindhoven. 2002.
[18] R. Krishna and R. Baur, "Analytic solution of the Maxwell-Stefan equations for multicomponente permeation across a zeolite membrane", Chem. Eng. J., Vol. 97, pp. 37-45.2004.
[19] S. Dhaval, Pervaporation of solvent mixtures using polymeric and zeolitic membranes: separation studies and modeling, Thesis Doctor of Philosophy at the University of Kentucky, 2001.
[20] L. Li, Z. Xiao, S. Tan, L. Pu and Z. Zhang, "Composite PDMS membrane with high flux for the separation of organics from water by pervaporation", Journal of Membrane Science, Vol. 243, pp.177-187, 2004.
[21] D. Hofmann, L. Fritz and D. Paul, "Molecular modelling of pervaporation separation of binary mixtures with polymeric membranes", Journal of Membrane Science, Vol. 144, pp. 145-159. 1998.
[22] S. Takegami, H. Yamada and S. Tsujii, "Pervaporation of ethanol/water mixtures using novel hydrophobic membranes containing polydimethylsiloxane", Journal of Membrane Science, Vol. 75, pp.93-105, 1992.
[23] B. Smitha, D. Suhanya, S. Sridhar and M. Ramakrishna, "Separation of organic-organic mixtures by pervaporation-a review", Journal of Membrane Science, Vol. 241, pp.1-21. 2004.
[24] T. Sano, H. Yanagishita, Y. Kiyozumi, F. Mizukami and K. Haraya, "Separation of ethanol/water mixture by silicalite membrane on pervaporation", Journal of Membrane Science, Vol. 95, pp. 221-228, 1994.
[25] M. Nomura, T. Yamaguchi and S. Nakao, "Ethanol/water transport through silicalite membranes", Journal of Membrane Science, Vol. 144, pp.161-171, 1998.
[26] T. C. Bowen, R. D. Noble and J. L. Falconer, "Fundamentals and applications of pervaporation through zeolite membranes", Journal of Membrane Science, Vol. 245, pp. 1-33, 2004.
[27] S. L. Wee, C. T. Tye and S. Bhatia, "Membrane separation process-Pervaporation through zeolite membrane", Separation and Purification Technology, Vol. 63, pp. 500-516. 2008.
[28] P. Izak, L. Bartovska, K. Friess, M. Sıpek and P. Uchytil, "Description of binary liquid mixtures transport through non-porous membrane by modified Maxwell-Stefan equations", J. Membr. Sci. Vol. 214, pp. 293-309, 2003.
[29] R. Rautenbach, C. Herion and U. Meyer-Blumentoth, "Pervaporation membrane separation processes", R.Y.M. Huang (Ed.), Membrane Science and Technology Series, Vol. 1, Chapter 3, pp. 181-191, 1990.
[30] A. Salem, A. A. Ghoreyshi and M. Jahanshahi, "A multicomponent transport model for dehydration of organic vapors by zeolite membranes", Desalination. Vol.193, pp. 35-42, 2006.
