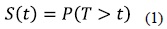
Remuestreo Bootstrap y Jackknife en confiabilidad: Caso Exponencial y Weibull
Bootstrap and Jackknife resampling in reliability: Case Exponential and Weibull
Reamostragem Bootstrap e Jackknife em confiabilidade: Caso Exponencial e Weibull
Javier Ramírez-Montoya*, Ignacio Osuna-Vergara**, Jessica Rojas-Mora***, Stalyn Guerrero-Gómez****
* M.Sc. Universidad de Sucre (Sincelejo-Sucre, Colombia). javier.ramirez@unisucre.edu.co.
** Universidad de Córdoba (Montería-Córdoba, Colombia). iosuna@correo.unicordoba.edu.co.
*** Universidad de Córdoba (Montería-Córdoba, Colombia). jmrojas@correo.unicordoba.edu.co.
**** M.Sc. (c) Universidad Santo Tomás (Bogotá-Distrito Capital, Colombia). stalynguerrero@usantotomas.edu.co.
Cómo citar este artículo: J. Ramírez-Montoya, I. Osuna-Vergara, J. Rojas-Mora & S. Guerrero-Gómez, "Remuestreo Bootstrap y Jackknife en confiabilidad: Caso Exponencial y Weibull", Rev. Fac. Ing., vol. 25 (41), pp. 55-62, ene.-abr. 2016.
Fecha de recepción: 15 de septiembre de 2015 Fecha de aprobación: 19 de diciembre de 2015
Resumen
Se comparan los métodos de remuestreo Bootstrap-t y Jackknife delete I y delete II, utilizando los estimadores no paramétricos de Kaplan-Meier y Nelson-Aalen, que se utilizan con frecuencia en la práctica, teniendo en cuenta diferentes porcentajes de censura, tamaños de muestra y tiempos de interés. La comparación se realiza vía simulación, mediante el error cuadrático medio.
Palabras clave: Bootstrap, Jackknife, Función de confiabilidad.
Abstract
In this paper the resampling methods bootstrap-t, Jackknife delete I and delete II, are compared using the non parametric estimators Kaplan-Meier and Nelson-Aalen, frequently used in the practice, taking into account different percentages of censorship, sample sizes and times of interest. The comparation is carried out by simulation, using the mean square error.
Keywords: Bootstrap, Jackknife, Reliability Function.
Resumo
Comparam-se os métodos de reamostragem Bootstrap-t e Jackknife delete I e delete II, utilizando os estimadores não paramétricos de Kaplan-Meier e Nelson-Aalen, que se utilizam com frequência na prática, tendo em conta diferentes porcentagens de censura, tamanhos de amostra e tempos de interesse. A comparação realiza-se via simulação, mediante o erro quadrático médio.
Palavras chave: Bootstrap, Jackknife, Função de confiabilidade.
I. Introducción
Cuando en la industria, y en particular en ingeniería, se modela el tiempo de ocurrencia de un evento de interés (tiempo de falla) de un circuito, estructura, componente, etc., uno de los objetivos principales es encontrar la mejor estrategia para estimar la función de confiabilidad o, también llamada, de supervivencia, para lo cual las técnicas de remuestreo son una buena alternativa, debido a sus propiedades asintóticas; sin embargo, teniendo en cuenta las situaciones extremas de porcentajes de censura altos, las estimaciones son afectadas de manera significativa.
Este trabajo presenta la situación en la que los tiempos observados y censurados pueden ajustarse a un modelo de probabilidad conocido de una distribución de Weibull y Exponencial, que en el área de la industria suceden a menudo, debido a las bondades del comportamiento de la función hazard de dichas distribuciones (creciente, decreciente, constante); por lo tanto, el interés se centra en la determinación del método de remuestreo, bootstrap o jackknife delete I y delete II, que presente los mejores resultados en dichos escenarios. En la actualidad no se encuentran trabajos que comparen simultáneamente en cuanto a Confiabilidad estas estrategias de remuestreo; un trabajo relacionado es el de Arrabal et al. [1], pero en otro contexto.
II. Función de confiabilidad
Cuando se tienen tiempos de falla, de los cuales k < n son observados, estimar la función de confiabilidad, dada por:
definida como la probabilidad de que un sistema o componente desarrolle sus funciones bajo condiciones de operación, por un período específico de tiempo [5].
Todos los tiempos de falla en confiabilidad no siempre se recogen durante un corto período de tiempo, ya que ocurre un fenómeno llamado censura, que hace que solo se tenga información parcial del tiempo de falla, afectando considerablemente la estimación. Existen diferentes tipologías de censura; este trabajo trata el caso de la censura a derecha, representando los experimentos en los que al finalizarlos, a algunas unidades estudiadas no les ocurre el evento de interés.
En caso de desconocimiento distribucional del tiempo de interés, la estimación no paramétrica resulta de mucha ayuda; en este trabajo se utilizan los estimadores:
A. Kaplan-Meier:
Donde nj es el número de individuos en riesgo en tj, es decir, el número de individuos vivos y no censurados justo antes de tj. Cualquier individuo con tiempo de censura registrado igual a tj será incluido en el conjunto de nj individuos en riesgo en tj, como individuos que murieron en tj. Esta convención es razonable, puesto que un individuo censurado en el tiempo tc falla por evento de interés después de tc [4].
B. Nelson-Aalen:
Proponen estimar la función de confiabilidad como:
con
Denominada función hazard acumulada. Ramírez [8] sugiere utilizar el estimador de Nelson-Aalen en muestras pequeñas.
III. Remuestreo Bootstrap en confiabilidad
Usando remuestreo bootstrap, propuesto por Efron [2], en los estimadores definidos en (2) y (3) se siguen los siguientes pasos:
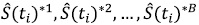para cada una de las B muestras bootstrap.Donde š(ti)* corresponde al promedio de la estimación< de la función de confiabilidad evaluada en cada tiempo ti de las muestras bootstrap; el procedimiento se realiza con base en el tiempo de interés primer cuartil.
IV. Remuestreo Jackknife en confiabilidad
A. Jackknife Delete - I
Una de las primeras técnicas para obtener los estimadores estadísticos fiables es Jackknife. Supongamos que tenemos una muestra X= X1, X2,...,Xn) y un estimador θ= s (t). La técnica jackknife se centra en las muestras que dejan de lado una observación a la vez:
Para i= 1,2,…, n, estas son llamadas muestras Jackknife. La i-ésima muestra Jackknife consiste en el conjunto de datos eliminando la i-ésima observación. Sea θ(i) = s(x(i)) la i-ésima replicación Jackknife de θ.
La estimación del error estándar Jackknife se define:
B. Método Jackknife Delete-d
En lugar de dejar una observación a la vez, dejamos de lado las observaciones d; por lo tanto, el tamaño de delete-d muestras Jackknife es (n - d).
La expresión de la estimación del error estándar del jackknife delete-d es:
Donde
es el promedio de las estimaciones de todos los subconjuntos s de tamaño (n - d) sin reemplazo para X1, X2,...,Xn.
V. Estudio de simulación
Se generaron muestras artificiales mediante un algoritmo en R, considerando tiempos observados y censurados Exponencial, Weibull y combinaciones, con tiempo de interés el primer; luego, se generaron muestras de tamaño con porcentajes de censura correspondientes al, y finalmente se calculó el de la función de supervivencia con los métodos de remuestreo en el estudio.
Se generaron 200 muestras mediante simulación de Monte Carlo, con 500 remuestras bootstrap. Teniendo en cuenta que los métodos de remuestreo Bootstrap y Jackknife a los estimadores no paramétricos tienen funcionalidades diferentes en el cálculo de estimación de error estándar, la comparación de dichas estrategias mediante simulación se considera la más adecuada en este estudio.
VI. Resultados
Para mostrar la eficiencia que tienen los métodos de remuestreo se presentan inicialmente los resultados de los intervalos de confianza mediante la amplitud y las coberturas reales de simulación. En la situación más extrema, con menor tamaño muestral, utilizando un nivel nominal del 95%.
En la Tabla I se observa que los I.C. mediante remuestreo bootstrap al estimador de Nelson-Aalen resultan ser un poco más precisos que los de las demás estrategias, seguidos de bootstrap al estimador de Kaplan-Meier; esto indica que los I.C. mediante bootstrap en muestras pequeñas presentan los mejores resultados.
Por otra parte, es de destacar que, con las estrategias de remuestreo a través de cualquier estimador, las coberturas reales de simulación son mayores a las nominales, debido a la amplitud de los intervalos, sin embargo, teniendo en cuenta los dos criterios simultáneamente se pueden sugerir como intervalos las mejores estrategias de la Tabla I. Finalmente, para tener más objetividad en la escogencia de las mejores estrategias de remuestreo, ya que los intervalos pueden ser sesgados, como este caso en la que la opción utilizada en el argumento de R, type=norm, se recomienda calcular los errores cuadráticos medios como medida general de eficiencia.
Estos comportamientos se presentan de forma similar en tamaños de muestra n = 50 y 100.
Luego, ilustrando los resultados para los errores cuadráticos medios se obtiene lo siguiente:
En la Gráfica 1, cuando se aumentan los porcentajes de censura las estimaciones son considerablemente afectadas; además, la estrategia de remuestreo Jackknife delete II a través del estimador de Nelson-Aalen presenta mejores resultados, seguida de Jackknife delete II a través del estimador de Kaplan-Meier; esto indica una mejoría en las estimaciones sobre las estrategias comunes usadas en confiabilidad, independientemente del porcentaje de censura.
Por otra parte, se notan unas posibles agrupaciones sobre los resultados de los errores cuadráticos medios, es decir, un grupo de estrategias de remuestreo Bootstrap y otro de estrategias de remuestreo Jackknife.
En la Gráfica 2 se observa que cuando se aumenta el tamaño muestral a n=50, se enmarcan de forma más clara las agrupaciones de los resultados de los errores cuadráticos medios, para los casos Bootstrap y Jackknife, siendo los últimos más eficientes.
Para resumir la ilustración de los resultados en cada estrategia de remuestreo, se presentan las Gráficas 3, 4, 5, 6, 7 y 8. Notando que en las Gráficas 3, 4, 6 y 7 la velocidad de disminución de los errores cuadráticos medios es mayor frente a las Gráficas 5 y 8, lo que confirma que la ganancia en la disminución del error cuadrático medio del método de remuestreo Jackknif frente al método Bootstrap se obtiene en muestras pequeñas.
VII. Conclusiones
Cuando se tienen muestras pequeñas y observaciones completas, la técnica de remuestreo Jackknife delete I presenta mejores resultados a través del estimador de Nelson-Aalen.
Cuando se tienen observaciones censuradas, los mejores resultados se obtienen con la técnica de remuestreo Jackknife delete II a través del estimador Nelson-Aalen.
Las amplitudes de los intervalos de confianza mediante remuestreo bootstrap resultan ser mejores.
La velocidad con que disminuyen los errores cuadráticos medios mediante la técnica de remuestreo Bootstrap es mayor a Jackknife.
Los métodos de remuestreo en las condiciones de este estudio resultan ser muy eficientes sobre la cobertura de los Intervalos de confianza.
Agradecimientos
Los autores del presente trabajos agradecen de manera muy especial a la Universidad de Sucre, Universidad de Córdoba y Universidad Santo Tomás por todo el apoyo, además de los árbitros por sus valiosas sugerencias.
Referencias
[1] C. Arrabal, R. Da Rocha, R. Nonaka, S. Meira. "Comparison of resampling method applied to censored data", International Journal of Advanced Statistics and Probability, Vol. 2, No. 2, pp. 48-55. 2014. DOI: http://dx.doi.org/10.14419/ijasp.v2i2.2291.
[2] B. Efron. "Bootstrap methods: Another look at jackknife", The Annals of Statistics, Vol. 7, pp. 1-26. 1979. DOI: http://dx.doi.org/10.1214/aos/1176344552.
[3] E. Kaplan and P. Meier. "Estimation from Incomplete Observations", American Statistical Association, Vol. 53, pp. 457-481. 1958. DOI: http://dx.doi.org/10.1080/01621459.1958.1050 1452.
[4] J. Lawless. Statistical Models and Methods for Lifetime Data. New York: Wiley and Sons, 2003.
[5] W. Meeker, L. Escobar. Statistical Models and Methods for Reliability Data. N.Y. John Wiley & Sons. 1998.
[6] W. Nelson. "Hazard plotting for incomplete failure data". Journal of Quality Technology, Vol. 61, pp. 27-52. 1969.
[7] R. Development Core Team. R: A Language and Environment for Statistical Computing". 2007. R Foundation for Statistical Computing, Vienna, Austria. Avalaible: http://www.Rproject.org.
[8] J. Ramírez. "Comparación de intervalos de confianza para la función de supervivencia con censura a derecha". Revista Colombiana de Estadística, Vol. 34, pp. 197-209. 2011.
