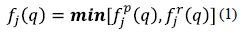
Solución del problema de ruteo de vehículos con demandas estocásticas mediante la optimización por espiral
Solving the vehicle routing problem with stochastic demands using spiral optimization
Solução do problema de roteamento de veículos com demandas estocásticas mediante a otimização por espiral
Natalia Alejandra Gelves-Tello*, Ricardo Andrés Mora-Moreno**, Henry Lamos-Díaz***
* Universidad Industrial de Santander (Bucaramanga - Santander, Colombia). natalia.gelves@correo.uis.edu.co.
** Universidad Industrial de Santander (Bucaramanga - Santander, Colombia). ricardo.mora1@correo.uis.edu.co.
*** Ph.D. Universidad Industrial de Santander (Bucaramanga - Santander, Colombia). hlamos@uis.edu.co.
Cómo citar este artículo: N. A. Gelves-Tello, R. A. Mora-Moreno and H. Lamos-Díaz, "Solución del problema de ruteo de vehículos con demandas estocásticas mediante la optimización por espiral", Rev. Fac. Ing., vol. 25 (42), pp. 7-19, may.-ago. 2016.
Fecha de recepción: 15 de octubre de 2015 Fecha de aprobación: 28 de marzo de 2016
Resumen
El artículo presenta los resultados del estudio de un problema de ruteo de vehículos con demandas estocásticas (Vehicle Routing Problem with Stochastic Demands, VRPSD), en el cual la única variable estocástica es la demanda de los clientes; esta variable sigue una distribución discreta, y su valor solo es conocido cuando el vehículo llega a la ubicación del cliente. Para su solución, se implementó la metaheurística denominada Optimización por Espiral, con el enfoque a priori y la estrategia de reabastecimiento preventivo para un solo vehículo. Para mejorar el método se inicializaron las rutas mediante la heurística del vecino más cercano, y posteriormente se utilizó la mutación, un operador evolutivo, para ampliar la zona de exploración de los puntos de búsqueda. Adicionalmente, se utilizó el intercambio 2-Opt, una heurística de búsqueda local, con el fin de intensificar la búsqueda en la vecindad de soluciones óptimas encontradas. Por otra parte, se realizó un diseño de experimentos 23, con el fin de determinar la influencia de cada factor en la función objetivo. Este análisis se llevó a cabo en 8 instancias diferentes que fueron diseñadas y desarrolladas por Galván et al. [1]. Finalmente, se compararon los resultados obtenidos con los arrojados por el algoritmo híbrido EPSO, con el objetivo de probar la eficiencia y eficacia del algoritmo desarrollado. Esta comparación evidenció que el método propuesto obtiene mejores resultados en todas las instancias, con mejoras de hasta el 5,71 %.
Palabras clave: demandas estocásticas, metaheurísticas, optimización por espiral, ruteo de vehículos.
Abstract
This paper presents a research work that studied a Vehicle Routing Problem with Stochastic Demands (VRPSD), in which the customer demand is the unique stochastic variable. Moreover, this variable follows a discrete distribution, and its value is only known when the vehicle arrives to the customer location. To solve this problem, we implemented the metaheuristic called Spiral Optimization, with an apriority approach and the preventing restocking strategy by only one vehicle. In order to improve that methodology, the Nearest Neighbor heuristic methodology was used, and later the Mutation, an evolutionary operator to widen the search points' exploration zone. Besides, the mutation and exchange 2-Opt (a local search heuristic) were applied for enhancing algorithm search strategies of diversification and intensification, respectively. On the other hand, it was carried out a design of experiments 23, in order to determine the effect of each input parameter on the objective function. The eight different instances used for this DOE, were designed and developed by Galván et al. [1]. The final solutions obtained were compared with the ones obtained using the hybrid algorithm EPSO for proving the efficacy and efficiency of the developed method. The comparison showed that the proposed method, obtains better solutions in all instances and improvements of up to 5,71 %.
Keywords: metaheuristics, spiral optimization, stochastic demands, vehicle routing.
Resumo
O artigo apresenta os resultados do estudo de um problema de roteamento de veículos com demandas estocásticas (Vehicle Routing Problem with Stochastic Demands, VRPSD), no qual a única variável estocástica é a demanda dos clientes; esta variável segue uma distribuição discreta, e seu valor só é conhecido quando o veículo chega à localização do cliente. Para sua solução, se implementou a metaheurística denominada Otimização por Espiral, com o enfoque a priori e a estratégia de reabastecimento preventivo para um só veículo. Para melhorar o método se inicializaram as rotas mediante a heurística do vizinho mais próximo, e posteriormente se utilizou a mutação, um operador evolutivo, para ampliar a zona de exploração dos pontos de busca. Adicionalmente, se utilizou o intercâmbio 2-Opt, uma heurística de busca local, com o fim de intensificar a busca na vizinhança de soluções ótimas encontradas. Por outra parte, se realizou um desenho de experimentos 23, com o fim de determinar a influência de cada fator na função objetivo. Esta análise foi realizada em 8 instâncias diferentes que foram desenhadas e desenvolvidas por Galván et al. [1]. Finalmente, se compararam os resultados obtidos com os encontrados pelo algoritmo híbrido EPSO, com o objetivo de provar a eficiência e a eficácia do algoritmo desenvolvido. Esta comparação evidenciou que o método proposto obtém melhores resultados em todas as instâncias, com melhoras de até 5,71 %.
Palavras chave: demandas estocásticas, metaheurísticas, otimização por espiral, roteamento de veículos.
I. Introducción
La logística de la cadena de suministro se define como el conjunto de actividades, como transporte y control de inventarios, que se realizan para obtener la transformación de la materia prima en un producto terminado y ofrecerles valor agregado a los clientes. Dicha logística absorbe entre el 60 % y el 80 % de cada dólar que vende una empresa y, por lo tanto, es esencial para su estrategia competitiva y la generación de ingresos [2].
El transporte es una de las actividades más representativas de la cadena de suministro, ya que actualmente las empresas no logran operar sin el movimiento de sus materias primas o de sus productos terminados. Adicionalmente, el costo que genera dicha actividad es de alrededor del 50 % de los costos totales de la cadena de suministro [2]. Es por esto que es importante que las empresas realicen estudios detallados sobre el transporte de mercancías, para lograr la creación de una estrategia de distribución que minimice los costos producidos por el transporte y, a su vez, disminuya notoriamente los costos atribuidos a la cadena de suministro.
El problema de ruteo de vehículos (VRP, Vehicle Routing Problem) busca minimizar los costos de transporte que se presentan en la logística de la cadena de suministro [3]. El VRP consiste en un conjunto de clientes con demandas específicas, un depósito y una flota de vehículos con una capacidad determinada, de forma que se pretende encontrar la ruta que minimice costos y que comience y termine en el depósito. En este caso, la capacidad y las demandas son factores determinísticos [4]. Sin embargo, un problema de ruteo de vehículos donde todos los parámetros estén dados por sentado no asegura un correcto acercamiento y, por ende, una correcta solución al problema en la vida real. Es por esto que nace el problema de ruteo de vehículos estocásticos (VRPS, Vehicle routing problema stochastic), donde se consideran algunos de los parámetros como estocásticos, como, por ejemplo: la demanda de los clientes, el número de clientes y el tiempo de recorrido de un cliente i a otro cliente j.
Una de las variantes del VRPS es el problema de ruteo de vehículos con demandas estocásticas (VRPSD, vehicle routing with stochastic demands), el cual será estudiado en el presente artículo.
De acuerdo con Secomandi (2001) [5], en la literatura se han trabajo dos enfoques de servicio para la solución del VRPSD. El primero es el estático o de optimización a priori y el segundo es el enfoque dinámico o de reoptimización. Bajo el enfoque de ruta a priori se establecen rutas antes de conocer las demandas de los clientes, de forma que el vehículo distribuye la mercancía siguiendo la ruta de clientes establecida antes de iniciar el recorrido. Dado que la demanda de los clientes solo se sabe al momento de atenderlos, se puede presentar un fallo en la ruta, lo cual significa que el vehículo no tiene la mercancía necesaria para satisfacer la demanda del nodo actual; para esto, se presentan distintas estrategias que evitan la modificación de la secuencia planteada de forma a priori.
En el enfoque de reoptimización, el enrutamiento es denominado dinámico, dado que se establece a medida que se ofrece el servicio. Según la literatura, este enfoque es el más utilizado para el VRP, pero cuando se establece un VRPSD, presenta dificultades que se reflejan en esfuerzos y tiempos computacionales demasiado grandes [6].
Siendo tanto el VRP como cada una de sus variantes, problemas de optimización combinatoria con una complejidad computacional NP-HARD [4], se hace necesario aplicar algoritmos que garanticen la obtención de una solución "adecuada" en un tiempo computacional razonable. De esta manera, han surgido distintas metaheurísticas, como La Optimización por Espiral (Spiral Optimization), que está fundamentada en fenómenos naturales, como tornados o huracanes, y logra acercarse a una respuesta "óptima" del problema [7].
La presente investigación se enfocó en el uso de la metaheurística Optimización por Espiral para la solución de VRPSD, y el artículo está organizado de la siguiente manera: en la sección II se define el problema de ruteo de vehículos con demandas estocásticas; en la III se describe el método a utilizar para dar solución al problema; en la IV se establecen las etapas de la aplicación del algoritmo al VRPSD; en la V se detalla el diseño de experimentos realizado, y, por último, en la VI se presentan las conclusiones de la investigación.
II. Definición del problema de Investigación
El VRPSD es un problema de complejidad computacional NP-HARD, en el cual existen clientes con demandas estocásticas, lo que quiere decir que no se conoce la cantidad exacta que demandará cada uno; solo se conoce la distribución estadística que sigue dicha demanda; así, solamente cuando el vehículo llega al nodo, a servir al cliente, se conoce la demanda real de este; además, se imponen una serie de restricciones que se discuten enseguida:
El problema se puede formular mediante un grafo completo G ={V, A, C}, donde V= {0, 1, 2, … , n} es un conjunto de nodos o clientes, y el valor 0 equivale al depósito; A= {(i,j;):i,j ∈ V, i ≠ j} es el conjunto de arcos que unen los nodos, y C = {Cij i.j ∈ V,i} es una matriz que contiene los costos de viajar del nodo i al nodo j. Esta matriz es simétrica, lo que indica que cada arco tiene un costo tal que Cij = Cij y satisface la desigualdad triangular Cij. El vehículo, con la capacidad Q definida, debe satisfacer la demanda de los clientes teniendo en cuenta que se debe minimizar el costo total esperado del viaje.
Dada la demanda estocástica de los clientes ξi, i = 1, 2,3,…,n se tiene que la demanda sigue la siguiente distribución de probabilidad discreta y uniforme pik= (ξi = k), k =0,1,2,..., K ≤ Q.
En la presente investigación se utilizó un solo vehículo y se contempló el problema con una política de servicio denominada enfoque a priori, junto con la estrategia de reabastecimiento preventivo. En este sentido, la ruta a desarrollar se establece antes de iniciar el viaje.
Además, en el recorrido es posible que se presenten dos eventos:
De forma que si q < hj, el vehículo debe volver al depósito a realizar un abastecimiento y después dirigirse al cliente j.
Con base en lo anterior, y empleando el enfoque a priori con reabastecimiento preventivo, se tienen los siguientes costos [1]:
Dada las condiciones del problema, el vehículo iniciará su recorrido según la ruta definida a priori; después de servir completamente al cliente j, el vehículo tendrá una carga q menor a su capacidad total Q, que presentará un costo ƒj (q), definido como el costo esperado total desde el nodo j haciab adelante. Si Lj se define como el conjunto de todas las posibles cargas q que puede tener el vehículo después de atender al cliente j tal que q ∈ Lj, entonces satisface que:
Donde:
Y
Con las siguientes condiciones de frontera:
Tal que, ƒpj(q) representa el costo esperado de proceder directamente al siguiente nodo, contemplando el costo por fallo en la ruta, mientras ƒTj(q) representa el costo del abastecimiento preventivo.
Las ecuaciones (1), (2) y (3) son utilizadas para calcular el valor de la función objetivo de la ruta a priori definida. Así mismo, para cada ruta se realizaron diferentes escenarios, donde se contemplaron diferentes combinaciones de demandas de los clientes, con el fin de obtener el costo esperado del viaje. El costo total se calculó promediando los costos obtenidos para cada escenario.
III. Método optimización por espiral
La Optimización por Espiral es una metaheurística con un nuevo método de búsqueda multipunto; fue desarrollada por Kenechi Tamura y Keiichiro Yasura (2011), y, al igual que otras metaheurísticas conocidas, está basada en fenómenos naturales; es por ello que este método se basa en las espirales logarítmicas que se forman en las cáscaras de nautilius, tornados y huracanes.
En esta metaheurística, los puntos de búsqueda trazan trayectorias en forma de espiral alrededor de un centro común, que se irá actualizando a medida que algún punto de búsqueda encuentre una posición que le ofrezca un menor valor en la función objetivo. Debido a este comportamiento, la Optimización por Espiral cuenta con una diversificación en la fase inicial, la cual garantiza una búsqueda en toda la región, identificando las subregiones con altas posibilidades de contener las mejores soluciones, y una intensificación en la fase final, que centra la búsqueda en aquellas subregiones encontradas previamente con el fin de determinar la mejor solución de dichas subregiones [7].
En la Fig. 2 se muestra cómo se actualiza la posición de cada punto de búsqueda de acuerdo al centro de espiral vigente en un espacio de 2 dimensiones.
Además, es importante destacar que este método depende solamente de tres parámetros θ (ángulo de rotación), r (radio de convergencia) y m (el número de puntos de búsqueda por utilizar).
El modelo de rotación de la espiral logarítmica con centro variable es:
Para i= 1,2,3,...,m.
Donde:
xi (k): Posición del punto de búsqueda i en la iteración k
In: Matriz identidad para n dimensiones
X*: Punto de convergencia
Sn(r, θ) = r Rn (θ): Matriz estable para n dimensiones
r: Radio de convergencia
θ: Ángulo de rotación
Xi (k+1): Posición del punto de búsqueda i en la iteración k+1.
IV. Desarrollo del algoritmo para el VRPSD
A. Inicialización de parámetros
En esta etapa se establecen los parámetros propios de la Optimización por Espiral, se determina la instancia o experimento por evaluar y se establecen todos los parámetros pertenecientes al experimento, los cuales son: el número de clientes, la posición de los clientes (xj - yj), la demanda promedio (Dj) y la desviación estándar (Sj) de cada cliente, el valor umbral para cada cliente (hj), el número de clientes promedio antes de realizar un reabastecimiento preventivo (r) y la capacidad (Q) que tendrá el vehículo.
B. Cálculo de distancias euclidianas
Dado que ya se cuenta con la posición (xj - yj) de cada uno de los clientes, se procede a realizar una matriz cuadrada (clientes xclientes) que contenga las distancias euclidianas entre cada uno de estos, con el fin de facilitar posteriormente el cálculo del costo de cada ruta.
C. Inicialización de los puntos de búsqueda
Para la inicialización de los puntos de búsqueda, se compararon dos diferentes métodos: el primero consistía en establecer la ruta inicial de cada uno de los puntos de búsqueda de forma aleatoria, y el segundo, en aplicar la heurística del vecino más cercano, para así hallar la ruta inicial de todos los puntos de búsqueda. Por tanto, iniciando desde el depósito, el vehículo se dirige al cliente Cj, que es el más cercano; posteriormente, se dirige hacia el cliente más cercano respecto a su nueva ubicación (Cj), y así sucesivamente hasta visitar todos los clientes.
Para compararlos, se aplicó el algoritmo para cada una de las instancias, con cada método de inicialización. Los resultados se presentan en la Tabla 1. De acuerdo con estos, se confirma que cuando se inicia con la heurística se obtienen mejores resultados que cuando se inicia de forma aleatoria. La mayor diferencia porcentual se presenta en la instancia 2, con un valor de 120,15 %, mientras que la instancia 6, con un valor de 18,925 %, presenta la menor diferencia porcentual. Dado estos resultados, se opta por realizar la inicialización de los puntos de búsqueda mediante la heurística del vecino más cercano.
D. Demandas clientes por escenarios
Teniendo definidas las rutas que realizará el vehículo y sabiendo que con un número de escenarios de 100 la función objetivo tiende a estabilizarse, es necesario establecer el conjunto de demandas que presentará cada cliente en los distintos escenarios de acuerdo con su demanda promedio (Dj) y su desviación estándar (Sj). Esto se realiza mediante la elección de 100 valores presentes en el intervalo Dj, † Sj, donde todos los valores tienen la misma probabilidad de ser seleccionados.
E. Costo de los puntos de búsqueda
Para cada uno de los escenarios, se realiza el cálculo del costo, teniendo en cuenta si se presenta reabastecimiento preventivo o fallos en la ruta. El valor de cada escenario es almacenado, para posteriormente promediar estos valores y obtener el costo para cada punto de búsqueda.
F. Establecimiento de X*
Calculado el costo promedio para cada una de los puntos de búsqueda, se debe seleccionar el que presente el menor costo, y este se define como X*, que será el centro de rotación para todos los puntos de búsqueda en la iteración.
G. mejoramiento de la ruta
Para el mejoramiento de la ruta se utilizarán los operadores de mutación y la heurística 2-Opt.
1) Operador de mutación: En primera instancia, se utilizará el operador de mutación, con el fin de realizar una mayor exploración en el espacio de búsqueda y garantizar una mejor solución al problema.
Para este caso, la mutación se realizará a los m puntos de búsqueda utilizados en la primera mitad de las iteraciones planteadas. Existirán tres maneras de realizar la mutación y estas se seleccionarán de forma aleatoria para cada punto de búsqueda. Posterior a este proceso, se elegirán los m puntos de búsqueda (tanto mutados como no mutados) que tengan el mejor valor en la función objetivo.
Para realizar las tres mutaciones posibles, el primer paso es seleccionar dos valores aleatorios, que serán los puntos de inicio y fin de la mutación; el punto I será el menor entre los dos y será el inicio de la mutación, y el punto j será el mayor y el fin de la mutación. Posterior a esto, se elegirá la mutación a realizar entre mutación flip (vuelta), mutación swap (intercambio) y mutación slide (deslizamiento).
La mutación se realiza a la ruta de cada una de los m puntos de búsqueda. A continuación, se explica de forma gráfica cada una de las posibles mutaciones.
2) Heurística 2-Opt: En segunda instancia se utiliza la heurística 2-Opt con el fin de mejorar la ruta que tiene el menor costo. Es así como, a partir de la ruta X, contenida en el menor punto de búsqueda, se eliminan 2 arcos no adyacentes y se reconectan los 2 nodos libres, de forma que se crea una nueva ruta X'. Ahora, si el costo de esta nueva ruta es menor que el costo de la ruta inicial, se reemplaza la ruta X por la ruta X'.
Es importante destacar que, debido a la gran cantidad de tiempo computacional requerido para la solución del problema, se implementaron las siguientes
estrategias a fin de mitigar este efecto:
En la siguiente imagen se presenta un ejemplo del proceso que se realiza a la hora de aplicar el 2-Opt en el proceso.
H. Decodificación de la ruta
Teniendo presente que los puntos de búsqueda contienen las rutas establecidas para que el vehículo visite a los clientes, estos deben estar compuestos por número enteros que determinen los arcos i, j de la ruta que debe realizar el vehículo. Para la aplicación de la metaheurística es necesario convertir las rutas de los puntos de búsqueda de la forma discreta a la forma continua, de manera que esas rutas queden en un espacio de solución factible para la aplicación de la rotación.
Para realizar dicha decodificación se opta por la aplicación de la fórmula ofrecida por Geetha, Ganesan y Vanathi [8].
Donde:
Yij: j-ésima dimensión de la solución i-ésima
Xji: j-ésima dimensión de la partícula i-ésima en el espacio de solución
Xmin: Valor mínimo de frontera del valor posición del punto de búsqueda en el espacio de solución Xmax: Valor máximo de frontera del valor posición del punto de búsqueda en el espacio de solución
xmax: Valor máximo de frontera del valor posición del punto de búsqueda en el espacio de solución.
rand(): número aleatorio distribuido uniformemente en [0,1]
n : número de clientes
I) Actualización de la posición de los puntos de búsqueda
Teniendo las rutas en el espacio de solución de la metaheurística, se procede a la actualización de ellas; así, cada uno de los puntos de búsqueda rota alrededor del que obtuvo el menor costo, es decir, el punto de búsqueda que se ha denominado como X*.
A partir de la ecuación (5), cada punto de búsqueda se rotará para obtener m - 1 nuevas rutas que deberán evaluarse, esto dado que el punto X* quedará con los mismos valores, puesto que está rotando sobre él mismo.
J. Codificación de la ruta
Para la evaluación de las nuevas rutas obtenidas a partir de la rotación, es necesario volver a codificar las rutas de forma que pasen del espacio de solución de la metaheurística al espacio discreto que define los arcos i,j.
Es así como existe un vector Xi que contiene la posición de los puntos de búsqueda en el espacio continuo o espacio de solución de la metaheurística, y posteriormente existirá un vector Yi que contendrá los valores discretos o los arcos i,j. Para esto se utiliza la regla ROV (Rank Order Value), creada por Bo, Wang y Jing [9], en la cual se asigna la valoración de 1 al menor valor dentro del vector Xi (Smallest Position Value, SPV); posteriormente se asigna la valoración de 2 al segundo menor valor posición, y así sucesivamente para los demás valores del punto de búsqueda, con el fin de crear el vector Yi, que tendrá en la posición de cada valor el número asignado según la regla ROV.
K. Condición de parada
Para efectos comparativos, se estableció el mismo número de iteraciones empleado por Galván et al. [1]. Es así como el algoritmo detiene su ejecución luego de 100 iteraciones, siendo la solución del VRPSD el costo de la ruta obtenido en la última iteración.
V. Diseño de experimentos
A. Determinación de factores
El desempeño del algoritmo Optimización por Espiral depende de los siguientes factores:
Para determinar los niveles del número de puntos de búsqueda, se seleccionaron cinco posibles valores (20, 30, 40, 50, 60) y se ejecutó el programa 5 veces, con cada uno de estos valores para las instancias 1 y 7. De acuerdo con los resultados, se seleccionaron los niveles equivalentes a 20 y 30, debido a que con las otras alternativas se obtenían soluciones similares de la función objetivo, pero se aumentaba el tiempo computacional.
Para establecer los niveles del ángulo de rotación y el radio de convergencia, se realizaron todas las posibles combinaciones entre seis valores seleccionados para el ángulo de rotación (π/9, π/4.5, π/4, π/3, π/2.25, π/2) y tres valores para el radio de convergencia (0.9, 0.95, 0.99) y se ejecutaron 5 veces cada una de estas combinaciones, para las instancias 1 y 7.
Posteriormente, se seleccionaron los valores de (π/9 y π/4) y r (0,9 y 0,99), los cuales obtuvieron los menores costos. En la Tabla 2 se presentan los valores de los niveles de cada factor.
Teniendo los parámetros definidos, se realiza un diseño de experimentos factorial ; esto debido a que estos diseños se categorizan entre los más económicos y facilitan la búsqueda e identificación de los factores que ejercen los efectos principales sobre la función objetivo. Los 8 tratamientos por evaluar fueron obtenidos usando el software estadístico Statgraphics Centurion XVI.
Así mismo, es importante destacar las características del equipo de cómputo mediante el cual se ejecutó el programa.
En la Tabla 3 se presentan los resultados obtenidos en el diseño experimental, proporcionados por el software estadístico Statgraphics Centurion XVI. Cabe destacar que cada tratamiento fue replicado 5 veces para el cálculo del valor promedio de la función objetivo.
Por otro lado, para cada instancia se encuentra resaltado en rojo el menor costo de los obtenidos en cada uno de los tratamientos, el cual se utilizará para realizar la comparación del rendimiento del algoritmo.
A. Análisis del diseño experimental
El modelo de regresión correspondiente al diseño de experimentos se expresa a continuación:
Donde:
Y Es el costo total esperado
β Es el efecto medio global
β1x1 Es el efecto producido por el parámetro A, es decir, el ángulo de rotación
β2x2 Es el efecto producido por el parámetro B, es decir, el radio de convergencia
β3x3 Es el efecto producido por el parámetro C, es decir, el número de puntos de búsqueda
ε Es el error aleatorio
Teniendo los resultados del diseño experimental, es importante conocer la magnitud del efecto que ejerce cada uno de los factores sobre la función objetivo, con el fin de establecer el nivel para cada uno de ellos. Los resultados se presentan en la Tabla 4.
Usando el software estadístico Statgraphics Centurion XVI, se graficaron los efectos para cada instancia en un diagrama de Pareto estandarizado, con el fin de visualizar el impacto sobre la función objetivo. En la Fig. 7 se presenta dicho diagrama para la instancia 1. Cabe destacar que el diagrama es estandarizado, dada la existencia del valor ε en (7).
Adicionalmente, se identificaron los factores que ejercen un efecto significativo, los cuales se resaltan en color rojo en la Tabla 4. Para el caso de la instancia 1, el ángulo de rotación ejerce un efecto significativo, puesto que su valor se extiende más allá de la línea de referencia.
Por otro lado, en caso de que un efecto significativo sea positivo, es decir, que al pasar de un nivel bajo a un nivel alto el valor de la función objetivo aumenta, el factor debe ubicarse en un nivel bajo, debido a que el objetivo es minimizar la variable respuesta. En caso contrario, si existe un efecto significativo que es negativo, el factor debe asumir el valor establecido en el nivel alto.
B. Comparación del rendimiento del algoritmo
En primer lugar, se realiza la comparación de los resultados del algoritmo Optimización por Espiral básico con los obtenidos agregando los operadores de mutación y la heurística 2-Opt. En segundo lugar, se realiza la comparación de los resultados presentados en la tesis de maestría "Optimización por simulación basado en un sistema evolutivo de optimización de enjambre de partículas para el problema de ruteo de vehículos con demandas estocásticas", realizada por Galván et al. [1], y los alcanzados en la presente investigación. Dicha información se presenta en la Tabla 5.
Con base en dichos resultados, se evidencia la superioridad de la heurística 2-Opt y de los operadores de mutación respecto a la metaheurística básica.
Esto se debe a que la heurística 2-Opt aumenta la intensificación de la búsqueda alrededor de buenas soluciones encontradas, y los operadores de mutación favorecen la diversificación, ya que buscan mejores soluciones al abarcar una mayor región. Así mismo, se observa que, en todas las instancias evaluadas, el algoritmo híbrido desarrollado supera los resultados obtenidos por el algoritmo híbrido EPSO, con mejoras de hasta el 5,71 %.
VI. Conclusiones
Con base en los resultados obtenidos para las diferentes instancias y su respectiva comparación con el método EPSO, se valida que el algoritmo Optimización por Espiral es una metaheurística viable y eficaz para la solución del problema de ruteo de vehículos con demandas estocásticas.
Se establece la importancia de la aplicación de la heurística 2-Opt y de los operadores de mutación para la obtención de mejores valores de la función objetivo, ya que estos logran mejorar las estrategias de búsqueda de intensificación y diversificación del algoritmo, respectivamente.
A partir de los datos obtenidos en el diseño de experimentos, se evidencia que no existe una única combinación óptima para todas las instancias, sino que esta depende de las características propias de la instancia que se esté estudiando.
En cuanto al efecto de los parámetros, se observa que el radio de convergencia es el parámetro que más influye en el resultado obtenido, esto debido a que en las instancias 2, 5, 6 y 8 es este el único que genera un efecto significativo. Así mismo, el número de puntos de búsqueda es el parámetro con menor influencia, siendo significativo para una sola instancia.
Referencias
[1] S. Galván, J. Arias and H. Lamos, "Optimización por simulación basado en un sistema evolutivo de optimización de enjambre de partículas para el problema de ruteo de vehículos con demandas estocásticas". Tesis de Maestría. Universidad Industrial de Santander, Bucaramanga, Colombia. 2013.
[2] R. H. Ballou, Logística. Administración de la cadena de suministro. México: Prentice Hall, 2004.
[3] J. Sourabh and K. Sarabjit, "Comparative analysis of two different heuristics for model of VRP", Advances in Computing and Communication Engineering (ICACCE), Dehradun (India), pp. 124-127, May. 2015. DOI: http://dx.doi.org/10.1109/ICACCE.2015.87.
[4] J. M. Daza, J. R. Montoya and F. Narducci, "Resolución del problema de enrutamiento de vehículos con limitaciones de capacidad utilizando un procedimiento metaheurístico de dos fases", Revista EIA, n° 12, pp. 23-38. Dec. 2009.
[5] N. Secomandi, "A rollout policy for the vehicle routing problem with stochastic demands", Operations Research, vol. 49 (5), pp. 796-802, Oct. 2001. DOI: http://dx.doi.org/10.1287/opre.49.5.796.10608.
[6] M. Dror, G. Laporte and P. Trudeau, "Vehicle Routing with Stochastic Demands: Properties and Solution Frameworks", Transportation Science, vol. 23 (3), Aug. 1989. DOI: http://dx.doi.org/10.1287/trsc.23.3.166.
[7] K. Tamura and K. Yasuda, "Spiral Optimization. A new multipoint search method", Systems, Man, and Cybernetics (SMC), Anchorage (Alaska), pp. 1759-1764, Oct. 2011. DOI: http://dx.doi.org/10.1109/ICSMC.2011.6083926.
[8] S. Geetha, G. Poonthalir and P. T. Vanathi, "A Hybrid Particle Swarm Optimization with Genetic Operators for Vehicle Routing Problem", Journal of Advances in Information Technology, vol. 1 (4), pp. 181-188, Nov. 2010. DOI: http://dx.doi.org/10.4304/jait.1.4.181.188.
[9] B. Liu, L. Wang and Y. Jin, "An effective hybrid PSO-based algorithm for flow shop scheduling with limited buffers", Computers & Operations Research, vol. 35 (9), pp. 2791-2806, Sep. 2008. DOI: http://dx.doi.org/10.1016/j.cor.2006.12.013.