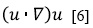que involucra la no linealidad de la velocidad y que, en general, es complejo de resolver.Estudio comparativo de flujo de fluido a través de una placa de orificio usando las ecuaciones de Stokes y de Navier-Stokes
Comparative study of fluid flow across orifice plate using Stokes and Navier-Stokes equations
Estudo comparativo de fluxo de fluido através de uma placa de orifício usando as equações de Stokes e de Navier-Stokes
Miryam Lucía Guerra-Mazo*, María Vilma García-Buitrago**, Elizabeth Rodríguez-Acevedo***
* M.Sc. Instituto Tecnológico Metropolitano (Medellín - Antioquia, Colombia). miryamguerra@itm.edu.co.
** M.Sc. Instituto Tecnológico Metropolitano (Medellín - Antioquia, Colombia). mariagarcia@itm.edu.co.
*** M.Sc. Instituto Tecnológico Metropolitano (Medellín - Antioquia, Colombia). elizabethrodriguez@itm.edu.co.
Cómo citar este artículo: M. L. Guerra-Mazo, M. V. García-Buitrago and E. Rodríguez-Acevedo, "Estudio comparativo de flujo de fluido a través de una placa de orificio usando las ecuaciones de Stokes y de Navier-Stokes", Rev. Fac. Ing., vol. 25 (42), pp. 99-110, may.-ago. 2016.
Fecha de recepción: 02 de julio de 2015 Fecha de aprobación: 25 de febrero de 2016
Resumen
Presenta los resultados de la comparación entre las ecuaciones de Stokes y de Navier-Stokes para la simulación del flujo de agua líquida, a condiciones atmosféricas, a través de una placa orificio concéntrica. A partir de los datos experimentales que fueron tomados en el banco de fluidos, se evaluaron las simulaciones de ambas ecuaciones, usando el software libre Freefem++cs, que se basa en el método de los elementos finitos; las variables evaluadas son velocidad y presión en un intervalo de tiempo. Al analizar los resultados obtenidos con las simulaciones y comparar con los datos experimentales se encontró que las ecuaciones de Navier-Stokes representan mejor el sistema que la ecuación de Stokes.
Palabras clave: ecuaciones de Stokes y Navier-Stokes, modelo matemático, placa de orificio, simulación.
Abstract
This paper presents the results of a comparison between Stokes and Navier-Stokes equations, in order to simulate the flow of liquid water at atmosferic conditions, through a concentric orifice plate. From experimental data taken from the fluids bank, the simulations of both equations were evaluated, using free software Freefem++CS, which is based on the finite elements method. The evaluated variables are velocity and pression in a time interval. When analyzing the results obtained with the simulations and comparing them with the experimental data, it was found that the Navier-Stokes equations represent better the system, than the Stokes equation.
Keywords: mathematical model, orifice plate, simulation, Stokes and Navier-Stokes equations.
Resumo
Apresenta os resultados da comparação entre as equações de Stokes e de Navier-Stokes para a simulação do fluxo de água líquida, a condições atmosféricas, através de uma placa de orifício concêntrica. A partir dos dados experimentais que foram tomados no banco de fluidos, se avaliaram as simulações de ambas as equações, usando o software livre Freefem++cs, que se baseia no método dos elementos finitos; as variáveis avaliadas são velocidade e pressão em um intervalo de tempo. Ao analisar os resultados obtidos com as simulações e comparar com os dados experimentais encontrou-se que as equações de Navier-Stokes representam melhor o sistema que a equação de Stokes.
Palavras chave: equações de Stokes e Navier-Stokes, modelo matemático, placa de orifício, simulação.
I. Introducción
Gracias a que los desarrollos en computación permiten hoy estudiar los sistemas reales mediante procesos de simulación y modelado, surge el interés de estudiar un dispositivo de medición de caudal usado comúnmente en procesos industriales, como lo es la placa orificio, que presenta ventajas por su sencillez de construcción, instalación, funcionamiento y mantenimiento, pero de la cual, sin embargo, se han documentado desventajas importantes en el uso industrial, tales como el rango de medida bajo, la generación de caídas de presión alta [1], la salida de señal no lineal con el flujo, variaciones ocasionadas por la instalación o manejo [2] y las causadas por los accesorios de las tuberías, que dan lugar a errores en la medición [3]. Al estudiar la placa orificio se busca establecer el modelo que mejor represente el sistema, lo cual podría permitir mejorar la señal de respuesta en este tipo de medidores de caudal.
El modelado es considerado [4] como la imitación de la operación de un proceso del mundo real o sistema sobre el tiempo y la simulación la historia artificial que permite hacer inferencias sobre el sistema real. Los modelos tradicionales para el análisis de flujo de fluidos son las ecuaciones de Stokes y Navier-Stokes, por lo que este documento relata el uso de ambos modelos matemáticos para la simulación del flujo a través de la placa orificio. Con el objetivo de evaluar el modelo que mejor representa el sistema, los resultados obtenidos se compararan con las mediciones del proceso real.
Para realizar el análisis del comportamiento del fluido a través de la placa orifico, se utilizó el software Freefem++cs, que es de uso libre [5]; en él se implementan las ecuaciones de Stokes y Navier-Stokes en su forma débil, y se resuelven mediante el método de los elementos finitos.
El presente trabajo está organizado de la siguiente forma: un marco conceptual, donde se presentan estudios realizados usando los modelos y que se encuentran en la literatura; un análisis de modelos, donde se detalla el equipo real donde se tomaron los datos del proceso, así como la descripción del modelo matemático, y se finaliza con los resultados experimentales y el comportamiento fluido-dinámico a través de las simulaciones.
II. Marco conceptual
Desde la época de Arquímedes de Siracusa (Sicilia), la humanidad ha dedicado mucho tiempo a comprender el comportamiento de los fluidos, no solo de forma experimental, sino a través de ecuaciones matemáticas que le permitan predecir dicho comportamiento. Entre muchos autores, se destaca el aporte de Claude-Louis Navier y George Gabriel Stokes, quienes formularon la ecuación de Navier-Stokes, que son un conjunto de ecuaciones derivadas parciales no lineales de segundo orden. La ecuación de Stokes es una simplificación de la ecuación de Navier-Stokes; en ella se elimina el término convectivo(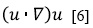 que involucra la no linealidad de la velocidad y que, en general, es complejo de resolver.
Debido a que las ecuaciones de Navier-Sokes y de Stokes no tienen una solución analítica, salvo en sistemas simples, se han utilizado métodos numéricos para resolverla, lo que se evidencia en la gran cantidad de investigaciones sobre el tema, entre ellas [7-9]; algunos sistemas donde se emplea la ecuación de Stokes [10-12], el uso de dicha ecuación ha permitido un mejor conocimiento de los sistemas tratados.
A pesar de que la ecuación Stokes es recomendada para bajas velocidades, no se debe descartar al iniciar el estudio del comportamiento de los fluidos, pues la conveniencia de modelar inicialmente con Stokes es una recomendación que puede ahorrar tiempo [11, 13], debido a que este modelo es más simple que el de Navier-Stokes, y, dependiendo el caso, podría llegar a resultados satisfactorios sin incluir el término convectivo.
Las ecuaciones de Navier-Stokes son consideradas en la actualidad uno de los seis problemas del milenio por el Clay Mathematics Institute [14, 15], por lo que no se debe escatimar esfuerzos en resolverlas y encontrar su aplicabilidad o no a diferentes problemas. En el caso de este trabajo, se consideró importante revisar la aplicabilidad de la ecuación de Stokes, con respecto a la de Navier-Stokes, sobre el estudio del comportamiento del fluido a través de una placa orificio, buscando evaluar si la información que arroja una ecuación con respecto a la otra es suficiente, o si para estos casos es necesario aplicar siempre las ecuaciones completas de Navier-Stokes.
III. Análisis de Modelos de stokes y de Navier-Stokes para flujo de fluidos
A. Descripción del sistema
El modulo experimental sobre el cual se toman los datos es el banco experimental del Laboratorio de Fluidos del ITM -Instituto Tecnológico metropolitano- (Fig. 1).
El sistema está compuesto por dos tanques interconectados a través de una tubería que permite la recirculación del fluido. La recirculación se realiza a través de dos bombas centrifugas. El banco cuenta con instrumentos de medida de presión diferencial y caudal, así como con un transmisor de flujo Signet 8550-1 que entrega la medida de caudal en galones por minuto, y con un sistema de adquisición de datos con un PLC marca Simantic S7-300 y CPU 314C-2DP, compacto con entradas y salidas digitales y analógicas integradas y un puerto PROFIBUS DP (maestro/esclavo).
En la Tabla 1 se consignan los parámetros del módulo experimental que fueron empleados en la simulación del comportamiento del fluido a través de la placa orificio del banco experimental.
La placa orificio utilizada es tipo concéntrico, y sus dimensiones se presentan en la Fig. 2.
B. Descripción del modelo matemático
La teoría matemática del medio continuo es un modelo idealizado y una abstracción para estudiar el comportamiento de los fluidos y sólidos a una escala superior a la atómica, donde se considera que los sistemas estudiados conservan sus características en todo punto, y en todo punto hay sistema; bajo esta consideración se establecen las ecuaciones de conservación de masa, momentum y energía que permiten analizar el sistema y establecer las ecuaciones que lo gobiernan.
A continuación, se realiza una breve descripción de cómo se deduce la ecuación de Navier-Stokes y, posteriormente, cómo se llega a la ecuación de Stokes. Partiendo de la segunda ley de Newton, de las ecuaciones de conservación del momentum y masa, unidas a las ecuaciones constitutivas o de comportamiento, se obtiene la ecuación de Navier-Stokes, y al eliminar el término convectivo, la ecuación de Stokes.
La segunda ley de Newton expresa que la fuerza (F) es igual a la masa (m) por la aceleración (a), que puede expresarse como la derivada de la velocidad (u) en relación al tiempo (t).
Teniendo en cuenta que la masa no tiene cambios con el tiempo, la ecuación anterior se puede escribir como:
La sumatoria de fuerzas externas (Fext) se descompone en fuerzas de cuerpo o volumen y fuerzas de contacto o superficiales.
En el caso de un medio continuo, la cantidad es el momentum o impulso en el fluido que ocupa el volumen Ω en el tiempo t. Donde ρ es la densidad.
Las fuerzas de cuerpo se asocian a una densidad de fuerza por unidad de volumen f, así:
Las fuerzas de contacto se analizan teniendo en cuenta el supuesto de Agustín Luis Cauchy [16], el cual considera una densidad superficial de fuerza II sobre la frontera Γt = &8706;Ωt.
Donde dS es la medida de superficie.
Reemplazando (4), (5) y (6) en (3) se llega a la expresión integral de la conservación del momentum:
A través del teorema de Cauchy [16], que relaciona la densidad de fuerza superficial con el tensor de esfuerzo, y del teorema de Gauss [17], que bajo condiciones de continuidad permite el cambio de la integral de superficie a integral de volumen, puede escribirse la expresión integral del momentum, como:
Donde S es el tensor de esfuerzos.
A nivel diferencial, queda:
Que puede escribirse:
Se tiene, además, del Teorema de Transporte de Reynolds [17], que:
Por tanto, la ecuación diferencial de conservación del momentum queda:
Teniendo en cuenta las ecuaciones de compatibilidad, se llega a definir el tensor de esfuerzos característico del fluido. Los fluidos newtonianos obedecen a los siguientes postulados [16]:
- Postulado de Stokes: El tensor de esfuerzos es función de S es función de υ a través de la matriz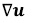 
en el mismo instante y punto. Esta es la conocida definición de esfuerzo cortante en un fluido, hecha por Newton.
- Postulado de Linealidad: La dependencia de S respecto a 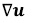es lineal (más precisamente, afín). Este postulado establece que las nueve componentes del tensor de esfuerzos pueden expresarse como función lineal de nueve variables, las componentes de esfuerzos Sij pueden expresarse como función lineal de nuevas variable, las componentes de .
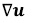τij Tiene inicialmente 81 coeficientes; dado que es simétrico, se reducen las nueve incógnitas a seis, obteniendo 54 coeficientes a ser determinados. Si se considera que el fluido es isotrópico y homogéneo, se disminuyen los coeficientes a dos constantes distintas en la dependencia de τ respecto 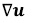[6].
De esta forma, a través de los postulados y consideraciones anteriores se tiene el teorema: existe una función ρ(x,t) y coeficientes λ y μ, tales que
Teniendo en cuenta la divergencia de S, se llega a la ecuación de Navier-Stokes
Si consideramos un fluido incompresible, como el Cuando se considera que la velocidad del fluido es agua, a baja velocidad (menores a 0.3 mach), donde baja comparada con las fuerzas viscosas, se desprecia las variaciones de densidad se ignoran [17], esto es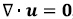 
entonces S queda
Así, para un fluido homogéneo, incompresible, viscoso, con densidad de fuerza de cuerpo dada por f= ρg, la ecuación de Navier-Stokes toma la forma:
Cuando se considera que la velocidad del fluido es baja comparada con las fuerzas viscosas, se desprecia el término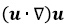 
, quedando la ecuación de Stokes,
Las ecuaciones (17), (18), (19) y (20) se simulan en el sistema de placa orificio. La solución del sistema se realiza a través del proceso numérico de elementos finitos. Se parte de las ecuaciones diferenciales (17), (18) y (19), (20), se transforman en su forma débil y teniendo en cuenta la geometría y condiciones de frontera se resuelven a través del software Freefem++cs.
La forma débil de las ecuaciones (17) y (18) es:
La forma débil de las ecuaciones (19) y (20) es:
IV. Resultados y discusión
A. Resultados experimentales
Las características de los instrumentos de medida utilizados para obtener los valores experimentales relacionados en la Tabla 2 fueron: dos manómetros de presión, marca Riester, con escala de 0 a 95 kPa, ubicados a una pulgada antes y después de la placa orificio, y un transmisor de flujo Signet 8550-1, que entrega la medida de caudal en galones por minuto.
Como se observa en la Tabla 2, hay una alta variabilidad en la medida de las presiones, debido a que la placa orificio es un sistema que restringe el área de flujo e introduce una alta perturbación en el flujo del fluido.
Para la simulación del sistema se tomaron en cuenta las propiedades del agua líquida a 15 °C, las cuales se describen en la Tabla 3; se tomó la gravedad estándar, g = 9.806 m/s2, y se consideró un caudal Q = 24 gal/min = 0.001514 m3, que, teniendo en cuenta el diámetro interior de la tubería Di = 56.4 mm, da una velocidad media de flujo u = 0.606 m/s.
A partir de los datos anteriores se simulan las ecuaciones de Navier-Stokes y de Stokes en su forma débil, obteniendo los siguientes resultados para la diferencia de presión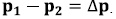 
En las Figs. 3 y 4 se observa que la simulación del sistema a través de la ecuación de Navier-Stokes es más adecuada para predecir el comportamiento del flujo del fluido que con la ecuación de Stokes, ya que representa mejor la fluctuación en la diferencia de presión (despreciando las condiciones de arranque, la fluctuación se mantiene entre 900 Pa y 1250 Pa), y la diferencia de presión media es cercana a la media experimental (1000 Pa). Se observa, además, que la simulación del sistema mediante la ecuación de Stokes no es apropiada para este tipo de sistemas, ya que al despreciar el término convectivo la diferencia de presiones tiende a cero con el paso del tiempo y esto no ocurre en el sistema real.
B. Comportamiento fluido-dinámico
Con el fin de comparar los perfiles de velocidad del fluido obtenidos en las simulaciones, se presentan a continuación algunas imágenes de velocidad de las ecuaciones de Navier-Stokes y de Stokes en diferentes tiempos, Fig. 5 y Fig. 6, respectivamente.
En la Fig. 5, de la ecuación de Navier-Stokes, se observa el cambio del perfil de velocidad conforme pasa el tiempo; debe destacarse que el flujo del fluido es irregular y que no se establece un perfil de velocidad estable, esto se debe al término convectivo, que es un término no lineal de la velocidad, el cual influye en los fenómenos de turbulencia en estos sistemas.
En la Fig. 6, donde se presentan las imágenes de velocidades del comportamiento del fluido bajo la ecuación Stokes en diferentes tiempos, no se observa variación del perfil de velocidad una vez se desarrolla.
En la simulación de la ecuación de Navier-Stokes se utilizó el comando convect del software Freefem++cs para la implementación del término convectivo, y aunque se logra una representación del sistema real que da un valor cercano a la media de diferencia de presión, no se logra representar la variabilidad, que es de 1000 Pa. La variación de la diferencia de presión media, en la simulación de la ecuación de Navier-Stokes, es aproximadamente de 175 Pa.
V. Conclusiones
El estudio reportado en este artículo ha sido realizado con el fin de investigar las similitudes y diferencias existentes para un flujo de fluido a través de una placa orificio a partir de las ecuaciones de Stokes y de Navier-Stokes. Las variables analizadas experimental y teóricamente fueron presión y velocidad.
Teniendo en cuenta los resultados, el término convectivo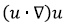 
en la ecuación Navier-Stokes es representativo en este tipo de sistemas y no debe despreciarse, como lo hace la ecuación de Stokes, ya que representa el fenómeno turbulento adecuadamente.
Es importante notar que, aunque según el estudio comparativo, las ecuaciones de Navier-Stokes se ajustan más al comportamiento real del sistema placa orificio, no lo representa completamente; por lo que a futuro sería conveniente ajustar numéricamente en la simulación términos que permitan definir con mayor precisión la dinámica del sistema a partir del modelo de Navier-Stokes.
Agradecimientos
Este trabajo se enmarca dentro del proyecto de investigación "Modelado y control no lineal de dinámica de fluidos a partir del desarrollo de un módulo experimental", clasificado con el código interno del ITM P14104.
A Jhon Alexander Isaza Hurtado y Adrián Felipe Martínez Pérez, por los aportes al trabajo.
Referencias
[1] J. M. Cimbala and Y. A. Cengel, "Flujo en Tuberías", Mecánica de Fluidos: Fundamentos y Aplicaciones. V.C. Olguin. Mexico: McGraw Hill, pp. 321-398, 2006.
[2] R. L. Mott, "Medición del Flujo", mecánica de Fluidos. J. E. Brito. Mexico: pearson Education, pp. 473-499, 2006.
[3] B. Manshoor, F. C. Nicolleau and S. B. Beck, "The fractal flow conditioner for orifice plate flow meters", Flow measurement and Instrumentation, vol. 22 (3), pp. 208-214, Jun. 2011. DOI: http://dx.doi.org/10.1016/j.flowmeasinst.2011.02.003.
[4] J. Banks, J. S. Carson, B. L. Nelson and D. M. Nicol, Discrete-event system simulation. USA: Prentice Hall, 2009.
[5] F. Hecht, O. Piro and A. Le Hyaric, "Freefem++," 2014. [Online]. Disponible: http://www.freefem.org/ff++/ftp/freefem++doc.pdf.
[6] R. Lewandowski, "The mathematical analysis of the coupling of a turbulent kinetic energy equation to the Navier-Stokes equation with an eddy viscosity", Nonlinear Analysis, Theory, methods & Applications, vol. 28 (2), pp. 393-417, Jan. 1997. DOI: http://dx.doi.org/10.1016/0362-546X(95)00149-P.
[7] M. M. Rhaman and K. M. Helal, "Numerical Simulations of unsteady Navier-Stokes Equations for incompressionable newtonian fluid using FreeFem++ based on Finite Element method", Annals of Pure and Applied Mathematics, vol. 6 (1), pp. 70-84, May. 2014.
[8] C. L. Felter, J. H. Walther and C. Henriksen, "Moving least squares simulation of free surface flows", Computers & Fluids, vol. 91, pp. 47-56, Mar. 2014. DOI: http://dx.doi.org/10.1016/j.compfluid.2013.12.006.
[9] Z. Li, K. Ito and M. C. Lai, "An augmented approach for Stokes equations with a discontinuous viscosity and singular forces", Computers & Fluids, vol. 36 (3), pp. 622-635, Mar. 2007. DOI: http://dx.doi.org/10.1016/j.compfluid.2006.03.003.
[10] T. Geenen, M. ur Rehman, S. P. MacLachlan et al., "Scalable robust solvers for unstructured FE geodynamic modeling applications: Solving the Stokes equation for models with large localized viscosity contrasts", Geochemistry, Geophysics, Geosystems. An Electronical Journal of the earth sciences, vol. 10 (9), pp. 1-12, Sep. 2009.
[11] A. Mojtabi and M. O. Deville, "One-dimensional linear advection-diffusion equation: Analytical and finite element solutions", Computers & Fluids, vol. 107, pp. 189-195, Jan. 2015. DOI: http://dx.doi.org/10.1016/j.compfluid.2014.11.006.
[12] J. Volker, K. Kaiser and J. Novo, "Finite Element methods for the Incompressible Stokes Equations with Variable Viscosity", Zeitschrift f¨ur Angewandte Mathematik und mechanik, vol. 96 (2), pp. 205-216, 2016. DOI: http://dx.doi.org/10.1002/zamm.201400291.
[13] P. Gómez-Palacio, "Solución de la ecuación de Stokes", Revista Universidad EAFIT, vol. 46, pp. 90-102, 2010.
[14] E. Engineering, Análisis y Simulación de la dinámica de fluidos computacionales-CFD a fluidos internos [Online]. Disponible: http://evaeng.com/analisis-y-simulacion-de-ladinamica-de-los-fluidos-computacionales-cfda-flujos-internos/.
[15] C. M. Institute, Navier-Stokes equation [Online]. Disponible: http://www.claymath.org/millennium-problems/navier%E2%80%93stokes-equation.
[16] J. L. Vázquez, Fundamentos matemáticos de la mecánica de fluidos. Madrid: Universidad Autónoma de Madrid, 2003.
[17] P. K. Kundu, I. M. Cohen and D. R. Dowling, Fluids mechanics. Elsevier, 2012.
