Desarrollo de un controlador PID por sintonización difusa aplicado a un sistema rotacional (péndulo invertido)
Development of a PID Controller by Tuning Fuzzy Applied to a Rotational System (Inverted Pendulum)
Desenvolvimento de um controlador PID por sintonização difusa aplicado a um sistema rotacional (pêndulo invertido)
Oscar Eduardo Gualdrón-Guerrero*, Kelvin de Jesús Beleño-Sáenz**, Danilo Alfonso López***
* Ph.D. Universidad de Pamplona (Pamplona-Norte de Santander, Colombia). oscar.gualdron@unipamplona.edu.co.
** M.Sc. Universidad Autónoma del Caribe (Barranquilla-Atlántico, Colombia). kelvin.beleno@uac.edu.co.
*** M.Sc. Universidad Francisco José de Caldas (Bogotá-Distrito Capital, Colombia). dalopezs@udistrital.edu.co.
Cómo citar este artículo: [1] O. E. Gualdrón-Guerrero, K. J. Beleño-Sáenz & D. A. López, "Desarrollo de un controlador PID por sintonización difusa aplicado a un sistema rotacional (péndulo invertido)", Fac. Ing., vol. 24 (40), pp. 95-105, Sep.-Dic. 2015.
Fecha de recepción: 19 de marzo de 2015 Fecha de aprobación: 20 de agosto de 2015
Resumen
El péndulo invertido ha sido un sistema de gran interés en el área del control y la academia; el modelado de este sistema presenta muchas dificultades asociadas a problemas de control en el mundo real. En este trabajo se expone una manera diferente de desarrollar una estrategia de control del sistema en mención, partiendo del diseño e implementación del sistema péndulo rotacional, pasando por su modelado utilizando estrategias de identificación de sistemas basados en métodos de inteligencia artificial, específicamente redes neuronales (N-FIR), y, finalmente, realizando la etapa de control por sintonización difusa a diferentes condiciones físicas provocadas en el péndulo (cambio de longitud y/o masa), siendo validados sobre el sistema real desarrollado, con buenos resultados.
Palabras clave: Inteligencia artificial, Péndulo invertido, Control inteligente, Identificación de sistemas, Sintonización difusa.
Abstract
The inverted pendulum system has arised a great interest in the control and academia areas; this system modeling presents many difficulties associated with the control problems in the real world. This paper presents a different way to develop a control strategy for the system in question, based on the design and implementation of the rotational pendulum system, then employing the same modeling strategies by using the system identification methods, based on the artificial intelligence neural networks (N-FIR), to finally taking the tuning fuzzy control step, for the different physical conditions caused on the pendulum (change in length and/or mass), which are validated, with good results on the real system developed,.
Keywords: Artificial intelligence, Inverted pendulum, Intelligent control, System identification, Fuzzy tuning.
Resumo
O pêndulo invertido tem sido um sistema de grande interesse na área do controle e dos acadêmicos; o modelamento deste sistema apresenta muitas dificuldades associadas a problemas de controle no mundo real. Neste trabalho se expõe uma maneira diferente de desenvolver uma estratégia de controle do sistema em menção, partindo do desenho e implementação do sistema pêndulo rotacional, passando por seu modelamento utilizando estratégias de identificação de sistemas baseados em métodos de inteligência artificial, especificamente redes neuronais (N-FIR), e, finalmente, realizando a etapa de controle por sintonização difusa a diferentes condições físicas provocadas no pêndulo (mudança de longitude e/ou massa), sendo validados sobre o sistema real desenvolvido, com bons resultados.
Palavras chave: Inteligência artificial, Pêndulo invertido, Controle inteligente, Identificação de sistemas, Sintonização difusa.
I. Introducción
En la actualidad se han generado sistemas muy complejos que requieren controladores altamente sofisticados para cumplir con el desempeño correcto bajo condiciones adversas. En ocasiones, la falta de conocimiento preciso acerca de algunos procesos es una problemática, debido al hecho de que los parámetros y la estructura de los sistemas cambian de manera significativa e impredecible, es decir, tienen una dinámica cambiante a través del tiempo [1-2].
Desde el punto de vista del control clásico, el desarrollo de controladores se diseña de acuerdo con el modelo matemático del sistema físico; se elige un modelo matemático que se asemeje al comportamiento de la dinámica del proceso, y de esta manera se aplican las técnicas de control. De tal manera que para un sistema dinámico cambiante la complejidad de diseñar un sistema de control bajo este tipo de circunstancias lleva a técnicas muy sofisticadas y rigurosas.
En este sentido, el péndulo invertido es un ejemplo paradigmático de un problema de ingeniería; un problema ante el cual el ingeniero, para alcanzar el objetivo propuesto, recurre a una síntesis entre las soluciones a los diferentes subproblemas en los que se descompone un proceso complejo. Estas distintas soluciones comprenden desde aspectos de concepción hasta cuestiones de implantación (que en este caso se traducen en la elección de sensores adecuados y en un sistema informático adecuado para procesar la información correspondiente). La labor del ingeniero consiste en integrar creativamente todos estos elementos y diseñar una solución concreta y eficiente al problema propuesto. Es notable observar que, en ese sentido, el péndulo invertido, siendo un sistema relativamente simple, aporta un ejemplo de máquinas mucho más complejas, como puede ser un robot o un automóvil [3-5].
De acuerdo con lo mencionado anteriormente, para el presente trabajo se desarrollaron varias etapas que permitieron implementar el control de un péndulo invertido (prototipo diseñado por los autores) más eficiente y preciso; se partió del diseño e implementación del sistema péndulo rotacional; luego se modeló, utilizando estrategias de identificación de sistema basados en métodos de inteligencia artificial, específicamente redes neuronales, y, finalmente, se realizó la etapa de control por auto-sintonización difusa a diferentes condiciones físicas provocadas en el péndulo (cambio de longitud y/o masa), siendo validados sobre el sistema real desarrollado.
II. Metodología
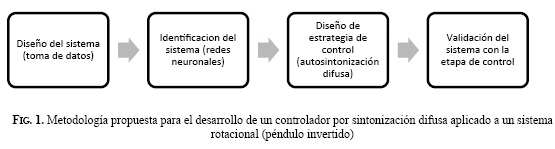
La Fig. 1 muestra la metodología planteada para el desarrollo de este trabajo, la cual cubre todas las etapas necesarias para el buen funcionamiento de la estrategia de control del sistema rotacional péndulo invertido; cada una de estas etapas se describen al detalle posteriormente, finalizando con los resultados de validación del sistema de control desarrollado sobre el prototipo diseñado por los autores.
A. Diseño, construcción y adquisición de datos del sistema
Para comenzar a hablar de estrategias de control, el primer paso es la obtención de un modelo o representación del comportamiento del proceso que se asemeje a las características reales del sistema dinámico; para esto se puede recurrir a representaciones matemáticas o a algoritmos de identificación mediante técnicas de inteligencia computacional, que facilitan la tarea sin necesidad de tener un conocimiento profundo del sistema por modelar y partiendo únicamente de los datos experimentales de entrada y salida del sistema. Con base en lo anterior se requiere realizar una medición directa del proceso bajo análisis, por lo cual fue necesario construir un modelo real del péndulo invertido (Fig. 2), con el fin de obtener las señales necesarias para la identificación.
Para la adquisición de datos se analizaron tres condiciones diferentes generadas bajo cambios de masa o longitud del péndulo, siguiendo el diagrama esquemático (Fig. 2). Para esta etapa se utilizaron como herramientas de adquisición las tarjetas DAQ NI USB 6210. De forma detallada, el proceso que se ha seguido para la adquisición de datos en el sistema es el siguiente:
Se comienza por colocar el péndulo en posición vertical invertida con respecto al reposo; una vez verificadas las conexiones en el sistema, se inicia el proceso de adquirir las señales de voltaje provenientes del encoder, relacionadas con el ángulo sensado. Con dicha información de entrada, en el entorno del software labview se genera una señal de voltaje modulada por ancho de pulso PWM que alimenta el motor del carro, haciendo mover el péndulo hacia la izquierda y la derecha, proporcionando de esta manera los datos que nos interesan, los cuales son la entrada al sistema y su correspondiente salida, es decir, la relación ángulo de posición del péndulo vs. voltaje del motor. Estos datos son exportados a MATLAB, donde se almacena la información para luego ser utilizada en la siguiente etapa: el modelado e identificación de la planta.
1) Conjunto de medidas experimental: Los datos almacenados de entrada-salida del sistema fueron para tres condiciones diferentes, ya sea en la variación de longitud de péndulo o cambio en la masa colgante sobre la barra. Cabe recordar que el voltaje del motor es determinado mediante la relación sentido de giro (0 o 1) y señal PWM (0-100) generada de manera porcentual.
La Fig. 3 muestra una respuesta del modelo 1 ante una entrada aleatoria de voltaje y su respectiva respuesta en ángulo de posición del péndulo.
B. Diseño y desarrollo de las plantas (identificación de sistemas)
Los primeros resultados obtenidos para la identificación se hicieron mediante modelos lineales paramétricos, evaluando los resultados a través de estructuras autorregresivas con entrada externa (ARX) y estructuras autorregresivas de promedio móvil con entrada externa (ARMAX). Aunque los resultados estaban cercanos al 70% de representación con estos modelos de las señales originales provenientes de la planta, no fueron tenidos en cuenta, buscando explorar otras técnicas que permitieran llegar al 100%, si fuese posible, de identificación. Para ello se probaron los datos de las plantas con técnicas de identificación basadas en inteligencia artificial, específicamente, por medio de redes neuronales artificiales analizadas a continuación [6-9]:
Con el fin de tener un criterio para la validación en el proceso de identificación por medio de redes neuronales, se dividieron los datos en dos partes: el primer 80% para la identificación, y el restante 20% para la validación, de la siguiente manera:
Una vez se tiene el criterio de entrenamiento y validación del modelo por medio de este método, el siguiente paso corresponde a crear la arquitectura de la red neuronal apropiada para el proceso de identificación. Con la arquitectura clara, se procede a estimar el número de capas que conformará la red, al igual que el número de neuronas en cada una de estas. Para este procedimiento se consideró una red multicapa tipo MLP (Multilayer Perceptron), en la que se hace necesario ejecutar un modo de aprendizaje para establecer los pesos de la red y, enseguida, mantener los pesos fijos obtenidos tras el entrenamiento; este es realizado mediante el método de Levenberg- Marquardt [10-11].
Después de muchos ensayos, se decide escoger solamente dos datos de entrada a la red neuronal, correspondientes a diferentes retrasos de la señal de voltaje del motor. Este modelo tiene excelente respuesta tanto en el entrenamiento como en la validación, por lo cual es el modelo generado en el entorno Simulink de MATLAB. Se puede decir que el modelo estimado para cada una de las plantas neuronales corresponde a un Modelo FIR, convirtiendo a la red neuronal en un filtro adaptativo [12]. En el campo del Procesamiento de Señales, a dicho filtro se le conoce como Filtro Lineal de Respuesta a Impulsos Finitos (FIR), (Fig.5). Esta estructura es comúnmente usada, debido a que la salida depende únicamente de las entradas al sistema; si bien este tipo de sistema tiene la ventaja de ser completamente estable, al no tener ningún tipo de realimentación, su aplicación se ve limitada a sistemas donde su respuesta al impulso decae lo suficientemente rápido y el sistema mismo debe ser estable desde un principio [12].
A continuación se muestran los resultados obtenidos tanto en el entrenamiento como en la validación, aplicando el modelo neuronal FIR a cada una de las plantas correspondientes:
Los resultados obtenidos por la red neuronal FIR ocurren en valores similares a los presentados por la data real de cada planta propuesta en este capítulo, indicando que el modelo funciona de manera satisfactoria y comprobando su validez.
C. Diseño de los controladores utilizando autosintonización por lógica difusa
Este apartado se centró en el diseño de los controladores para cada uno de los modelos de identificación obtenidos anteriormente; los diseños pretenden usar técnicas de control inteligente, en las cuales el objetivo del controlador es conservar el péndulo invertido lo más cercano posible a la posición vertical y buscar la respuesta adecuada frente a perturbaciones pequeñas [13]. Para ello se han desarrollado Controladores Autosintonizables por Lógica Difusa (Fig. 7).
De acuerdo con el modelo de planta obtenido para el sistema de péndulo invertido, la variable por controlar es la posición del péndulo. El punto de equilibrio para esta posición es 180º (pi), que es la señal de referencia; tras la observación del rango de operación para la planta identificada, los valores máximos y mínimos de salida (posición angular del péndulo) varían entre 170º y -190º; teniendo presente estos valores, entonces, la señal de error para el controlador oscilará entre -10 y 10.
1) Sintonización y ajuste del controlador: Se realizó un control PID difuso con el propósito de que el controlador sintonizara los valores de Kp, Kd y Ki de manera automática; para estimar dichos valores se empleó una estrategia de lógica difusa. Para la estimación de Kp, en esta metodología, se usó como entrada el error y como salida el valor de esta misma variable; el valor de Ki se creó de manera idéntica al de Kp, con la particularidad de que se cambió el universo discurso y que la entrada fue la integral del error; finalmente, el valor de Kd se estimó teniendo como entrada la derivada del error y, al igual que en los anteriores casos, teniendo como salida la misma variable. Cabe destacar que se utilizó un criterio mínmáx para evaluar las reglas y que la de fuzificación se realizó con el método del centroide (Fig. 8).
En el controlador PID autosintonizable se generaban valores muy altos para la acción de control, los cuales no eran los adecuados para generar un error en estable cercano a cero, por lo cual fue necesario multiplicar la salida del controlador por una constante igual a 0.001; este valor fue hallado a través de prueba y error, ajustándolo conforme se variaba el universo discurso de cada bloque difuso. Después de multiplicar la salida del controlador por el valor de la constante se procedió a limitar dicha señal entre -24 y 24, debido a que corresponde al rango de trabajo del actuador, en este caso, el motor de corriente continua a 24V. Antes de introducir la señal de control al modelo estimado del péndulo invertido se introdujeron dos bloques más correspondientes a generar los retrasos necesarios con los cuales fue entrenada la red neuronal artificial para la identificación del sistema; esta red neuronal fue creada con el comando gensim, y se muestra con el nombre de PÉNDULO INVERTIDO en el diagrama de bloques de la Fig. 8. Finalmente, la salida de la planta se retroalimenta para obtener el error, y de esta manera estimar los valores correspondientes a Kp, Kd y Ki.
Acorde con los parámetros descritos anteriormente y tras la simulación de diagrama de bloques de control PID autosintonizable para cada planta neuronal identificada, a continuación se muestra cómo se adaptaron los valores de Kp, Kd y Ki en el período transitorio y la correspondiente salida de una de las plantas, siendo igual para las otras dos (Fig.9).
Las características del controlador difuso tipo PID autosintonizable se muestran claramente en las anteriores figuras; se debe aclarar que también se realizaron pruebas con controladores difusos tipo PI y tipo PD, pero los resultados obtenidos no fueron los mejores debido a que siempre se presentó un error en estado estacionario bastante considerable, por lo cual se descartaron estas opciones.
El tiempo de estabilización para cada modelo de identificación es diferente, ya que sus características varían (longitud o masa), por lo cual las constantes Kp, Kd y Ki en cada diseño se modifican y se adaptan de diversas formas hasta encontrar un valor estable, siendo estas las adecuadas para lograr finalmente el objetivo de control, que, en este caso, es llevar el péndulo al punto de referencia igual a 180 grados. La idea de esta estrategia de control es descubrir las constantes proporcional, integral y derivativa, con el fin de construir un diagrama de bloques de control PID convencional. Los valores exactos encontrados para las constantes mencionadas en cada una de plantas se muestran en la siguiente Tabla 2.
Después de aplicar las técnicas de control autosintonizable tipo PID y de obtener los valores deseados de las ganancias proporcionales, integrales y derivativas para cada planta, se hace necesario crear una nueva simulación (Simulink - MATLAB), reemplazando los bloques difusos de la sintonización por bloques de ganancia, los cuales tomarán el valor de las constantes halladas, convirtiendo este nuevo diagrama de bloques en un sistema de control PID convencional, con la particularidad de que la planta no es una función de transferencia o modelo matemático, sino un modelo neuronal; en la literatura, este tipo de estructuras pertenece a la familia de control neuronal indirecto [14-15]; en la Fig. 10 se presenta este tipo de estructura.
La siguiente acción es simular al esquema alcanzado para cada una de las tres plantas neuronales, tomando los valores correspondientes presentados en la Tabla 2 (Fig. 11). Si los resultados obtenidos por cada uno de los controladores son adecuados y siguen la señal de referencia dada, el siguiente paso, de acuerdo con la metodología planteada, será proceder a validar dichos controladores ante la presencia de perturbaciones.
Para verificar si el sistema de control PID convencional puede rechazar una perturbación se realiza un experimento manteniendo fijo el valor de la señal de la referencia (180). El experimento consiste en adicionar dos perturbaciones a la salida de la planta neuronal; la primera perturbación, de una amplitud igual a 2, y la segunda, de una amplitud igual -2; cada perturbación es adicionada en un determinado instante, siendo diferente en cada una de las plantas. Las perturbaciones son analizadas de manera independiente y simularán una condición que en el mundo real represente una ráfaga de viento que actúa sobre la masa colgante o una fuerza inesperada aplicada al carro. Si los controladores diseñados y sintonizados mediante la técnica descrita anteriormente rechazan las perturbaciones provocadas, y la salida del sistema logra recuperar el valor de referencia que se tenía antes de presentarse la perturbación, se valida el compensador diseñado; entonces se dice que finalmente la estructura del controlador diseñado y su sintonización satisfacen el problema de control planteado.
La adición de la perturbación para la primera planta neuronal se hace en el instante t=35; primero se evalúa el disturbio con amplitud positiva igual a 2, y en una segunda simulación se evalúa para una amplitud negativa igual a -2. Para la segunda planta neuronal la perturbación se realiza en el instante t=24, y la amplitud de los disturbios son de la misma magnitud que para la primer planta; de igual manera, se realizan dos simulaciones para cada disturbio generado. Los resultados obtenidos en la salida del sistema para cada uno de los controladores propuestos, bajo la agregación de un disturbio presente en la salida de la planta uno, se presentan a continuación ante un disturbio con amplitud positiva (Fig. 12). Para las otras dos plantas se obtuvieron, igualmente, excelentes resultados.
III. Conclusiones
La identificación de sistemas fue realizada usando técnicas de inteligencia computacional, como son las redes neuronales, seleccionando un modelo de identificación neuronal FIR, que utiliza una red neuronal tipo MLP, y entrenando el algoritmo por medio de la propagación de error hacia atrás o retropropagación (Backpropagation), acorde con la optimización de Levenberg-Marquardt, mostrando resultados de entrenamiento y validación eficaces en el momento de identificar cada una de las plantas generadas. Cabe señalar que las técnicas de identificación presentadas no son la única alternativa de solución; se propone también desarrollar la identificación por medio de modelos paramétricos lineales OE (output error), identificación por redes neuronales con modelo ARX y ARMAX e identificación por lógica difusa o neurodifusa (ANFIS).
En este trabajo se ha presentado el diseño de un tipo de controladores para las plantas diseñadas representativas de un sistema de péndulo invertido. Utilizando la técnica de autosintonización difusa tipo PID, la cual encuentra los valores de las ganancias apropiadas de manera automática para sintonizar un controlador convencional PID, demostrándose que los resultados obtenidos mediante esta técnica son buenos, ya que las respuestas de cada una de las plantas logran un error en estado estacionario nulo; además, los compensadores rechazan incluso una perturbación permanente presente en la salida de las plantas. Como se pudo observar, los controladores PID convencionales sintonizados mediante la técnica difusa son capaces de rechazar las perturbaciones tanto de amplitud positiva como negativa.
Por otro lado, con estas pruebas se ha demostrado que explorar otras alternativas de controladores permite llegar a unos buenos resultados con respecto a la salida de los sistemas, independientemente de las condiciones, como se hizo en este caso con tres diferentes situaciones. Es importante mencionar que cada uno de los diseños desarrollados parte del condicional de que el sistema funciona a ciertos rangos de ángulo superiores e inferiores, es decir, cuando el péndulo trabaja a ángulos mayores a la referencia se desestabiliza el sistema y los controladores diseñados no trabajan correctamente. Como trabajo futuro se espera realizar la misma estrategia, pero aplicando control no solo al ángulo del péndulo, sino también al carro del sistema.
Referencias
[1] R. M. Brisilla, V. Sankaranarayanan "Nonlinear control of mobile inverted pendulum". Robotics and Autonomous Systems, Vol. 70, pp. 145-155, August 2015.
[2] F. Dai, X. Gao, S. Jiang, W. Guo, "A twowheeled inverted pendulum robot with friction compensation", Mechatronics, Available online 4 July 2015.
[3] M. Olivares, P. Albertos, "Linear control of the flywheel inverted pendulum", ISA Transactions, Vol. 53, pp. 1396-1403, 2014.
[4] Z. Sun, N. Wang, Y. Bi, "Type-1/type-2 fuzzy logic systems optimization with RNA genetic algorithm for double inverted pendulum", Applied Mathematical Modelling, Vol. 39, pp. 70-85, January 2015.
[5] A. M. El-Nagar, M. El-Bardini, N. M. El-Rabaie, "Intelligent control for nonlinear inverted pendulum based on interval type-2 fuzzy PD controller", Alexandria Engineering Journal, Vol. 53, pp. 23-32, 2014.
[6] O. Gualdrón, C. Peña, C. Maldonado, "Identificación automática de cilindros de almacenamiento de gas utilizando redes neuronales tipo hop field", Revista Ingeniería de la Universidad Industrial de Santander, Vol. 11-1, pp. 101-109, 2012.
[7] A. Guerrero, O. Gualdrón, "Identificación de un modelo dinámico del generador de vapor de la caldera en la planta Termotasajero Colgener", Revista Colombiana de Tecnologías de Avanzada, Vol. 21, pp. 52-59, 2013.
[8] M. Romero Ugalde, J.C Carmona, J. Reyes, V. Alvarado, J. Mantilla, "Computational cost improvement of neural network models in black box nonlinear system identification", Neurocomputing, Vol. 166, pp. 96-108, 2015.
[9] E. Gómez, "Aplicación del modelo neurodifuso ANFIS vs. Redes Neuronales, al problema predictivo de caudales medios mensuales del río Bogotá en Villapinzón", Revista Tecnura, Vol. 14, pp. 18-29, 2010.
[10] P. Szymczyk, "Z-transform artificial neural networks", Neurocomputing, Vol. 168, pp. 1207-1210, 2015.
[11] J. S. Almeida, "Predictive non-linear modeling of complex data by artificial neural networks", Current Opinion in Biotechnology, Vol. 13, pp. 72-76, February 2002.
[12] E. Caicedo, J.A. López, M.A. Muñoz, Control Inteligente. Editorial Universidad del Valle, 2009.
[13] Z. Sun, R. Xing, C. Zhao, W. Huang, "Fuzzy auto-tuning PID control of multiple joint robot driven by ultrasonic motors", Ultrasonics, Vol. 46, pp. 303-312, 2007.
[14] I. Anastasios, A. Dounis, P. Kofinas, G. Papadakis, C. Alafodimos, "A direct adaptive neural control for maximum power point tracking of photovoltaic system", Solar Energy, Vol. 115, pp. 145-165, 2015.
[15] X. Ruan, M. Ding, D. Gong, J. Qiao, "Online adaptive control for inverted pendulum balancing based on feedback-error-learning", Neurocomputing, Vol. 70, pp. 770-776, 2007.