Metaheuristic algorithms for building Covering Arrays: A review
Algoritmos metaheurísticos para construir Covering Arrays: Revisión
Algoritmos metaheurísticos para construir Covering Arrays: Revisão
Jimena Adriana Timaná-Peña*, Carlos Alberto Cobos-Lozada**, Jose Torres-Jimenez***
* Esp. Universidad del Cauca (Popayán-Cauca, Colombia). jtimana@unicauca.edu.co.
** Ph.D. Universidad del Cauca (Popayán-Cauca, Colombia). ccobos@unicauca.edu.co.
*** Ph.D. Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional (Ciudad Victoria-Tamaulipas, México). jtj@cinvestav.mx.
Fecha de recepción: 19 de enero de 2016 Fecha de aprobación: 1 de junio de 2016
Abstract
Covering Arrays (CA) are mathematical objects used in the functional testing of software components. They enable the testing of all interactions of a given size of input parameters in a procedure, function, or logical unit in general, using the minimum number of test cases. Building CA is a complex task that involves lengthy execution times and high computational loads. The most effective methods for building CAs are algebraic, Greedy, and metaheuristic-based. The latter have reported the best results to date. This paper presents a description of the major contributions made by a selection of different metaheuristics, including simulated annealing, tabu search, genetic algorithms, ant colony algorithms, particle swarm algorithms, and harmony search algorithms. It is worth noting that simulated annealing-based algorithms have evolved as the most competitive, and currently form the state of the art.
Keywords: ant colony optimization; Covering Array; genetic algorithms; harmony search algorithm; metaheuristics; particle swarm optimization; simulated annealing; tabu search.
Resumen
Los Covering Arrays (CA) son objetos matemáticos usados en pruebas funcionales de componentes software. Los CA permiten probar todas las interacciones de un tamaño determinado, de los parámetros de entrada de un procedimiento, función o unidad lógica en general, usando el mínimo número de casos de prueba. La construcción de CA es una tarea compleja que requiere largos periodos de ejecución y gran capacidad computacional. Los métodos más efectivos para construir CA son los algebraicos, voraces y basados en metaheurísticas. Estos últimos son los que han arrojado mejores resultados hasta la fecha. Este artículo presenta una descripción de las contribuciones más importantes hechas por diferentes metaheurísticas, incluyendo el simulated annealing (recocido simulado), búsqueda tabú, algoritmos genéticos, algoritmo de la colonia de hormigas, algoritmo de enjambre de partículas y algoritmo de búsqueda armónica. Cabe anotar que los algoritmos basados en recocido simulado se han convertido en los más competitivos y actualmente son el estado del arte.
Palabras clave: algoritmo de búsqueda armónica; algoritmos genéticos; búsqueda tabú; Covering Array; metaheurística; optimización por colonia de hormigas; optimización por enjambre de partículas; recocido simulado.
Resumo
Os Covering Arrays (CA) são objetos matemáticos usados em provas funcionais de componentes software. Os CA permitem provar todas as interações de um tamanho determinado, dos parâmetros de entrada de um procedimento, função ou unidade lógica em geral, usando o mínimo número de casos de prova. A construção de CA é uma tarefa complexa que precisa longos períodos de execução e grande capacidade computacional. Os métodos mais efetivos para construir CA são os algébricos, vorazes e baseados em metaheurísticas. Estes últimos são os que têm produzido melhores resultados até esta data. Este artigo apresenta uma descrição das contribuições mais importantes feitas por diferentes metaheurísticas, incluindo o simulated annealing (recozimento simulado), busca tabu, algoritmos genéticos, algoritmo de colônia de formigas, algoritmo de enxame de partículas e algoritmo de busca harmônica. Deve-se observar que os algoritmos baseados em recozimento simulado têm-se convertido nos mais competitivos e atualmente são o estado da arte.
Palavras chave: algoritmo de busca harmônica; algoritmos genéticos; busca tabu; Covering Array; metaheurística; otimização por colônia de formigas; otimização por enxame de partículas; recozimento simulado.
I. Introduction
Over the past few decades, software testing has been the most widely used method for ensuring software quality [1]. The tests may be seen as a set of processes that are designed, developed and applied throughout the life of software development to detect and correct defects and faults found during and following the implementation of the code, and thus raise the quality and reliability of the program delivered to the end user [2]. However, applying thorough software tests that allow the testing of the software component in its entirety, as well as being both an expensive and timeconsuming task, is an almost impossible one. Even trying to test the simplest software, a large number of test cases can be generated due to the many possible combinations of input parameters. Creating test cases for all these possibilities is an unfeasible and impractical process [1, 2]. For example, if it is required to test a software component that receives as input parameters values from five sensors and each sensor can take 10 different values, 105 or 100,000 different test cases would then be required to exhaustively test that component.
Combinatorial tests provide an alternative to exhaustive testing, which select test cases by a sampling mechanism that systematically covers the combinations of input parameter values, defining a smaller set of tests that is relatively easy to manage and run [3]. This type of testing reduces costs, and significantly increases the effectiveness of software testing. However, the challenge for the combinatorial tests lies precisely in finding the minimum number of test cases that achieve maximum coverage with the minimum cardinality [4, 5]. One of the combinatorial objects that meets the criteria of coverage for this type of situation is Covering Arrays (CA) [5].
Covering Arrays are mathematical objects that have been widely used in the design of experiments in a range of sectors and application areas such as agriculture, medicine, biology, material design and manufacturing. They have the necessary properties to optimally define a series of experiments, due to their combinatorial nature [5]. Applied most recently to the area of software testing, CAs can be used and applied in the functional testing of software. One of the main applications of these objects is generating the smallest number of sets or software test cases to cover all interactions sets of input parameters of a procedure, function or software logical unit [5].
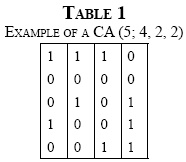
A Covering Array denoted by CA(N; k, v, t) is a matrix M of size N x k, where N (rows of the matrix) is the number of experiments or tests, k is the number of factors or parameters (of the method, function or unit of the procedure being evaluated), v is the number of symbols (possible values) for each parameter, referred to "alphabet", and t is the degree of interaction between parameters, called strength [6]. Each submatrix of size N x t contains each tuple of symbols of size t (t-tuple) at least once [5]. A CA is optimal if it contains the minimum possible number of rows [4] and is known as CAN. Table 1 shows an example of a CA (5; 4, 2, 2). The strength of this CA is 2 (t = 2), with four parameters or factors (k = 4), and an alphabet of 2 (v = 2) values that is defined by the symbols {0,1}. Note that in each pair of columns the combinations {0,0}, {0,1}, {1,0} and {1,1} appear at least once [5].
To illustrate the CA approach applied to the design of software testing, an example of a Web System to be tested using the parameters is presented in Table 2. In this example, we have 4 factors or parameters (k = 4) corresponding to the Browser, Operating System, Database Management System or DBMS, and the Connection System, each with 3 possible values (v = 3).
Table 3 shows part of an exhaustive test, in which all of the possible parameters (defining an interaction strength t = k, which in this case is 4) combinations are generated. The higher the degree of strength (t) and the number of values for each parameter (v), the greater the number of exhaustive tests to be performed. This number of tests is equal to vt. For the given example, to perform an exhaustive test, thereby covering 100% of cases, a total of 34 or 81 test cases would need to be defined.
However, if the interaction between these parameters is brought down to strength 2 (t = 2), the number of possible combinations is reduced to 32 or nine test cases, guaranteeing ample coverage in the test with the minimum possible effort [7]. Table 4 shows the CA (9; 4, 3, 2) resulting from the above example with strength 2 (t = 2) and alphabet 3 (v = 3). To make the mapping between the Web system and the CA, every possible value of each parameter in Table 2 is labeled by row number, in this case 0, 1, and 2. The combinations that must appear at least once in each subset of size N x t are: {0,0}, {0,1}, {0,2}, {1,0}, {1,1}, {1,2}, {2,0}, {2,1}, {2,2}.
Table 5 shows specifically the test cases or experiments to be performed. Note that each of the nine experiments is analogous to each row of the CA.
Building optimal CAs (CAs with the smallest possible size of rows) is a complex task that involves a considerable computational burden. To obtain CAs of a considerable size, the use of many processors in parallel for several months is generally required, but achieving its definition has a very significant impact on the processes that go on in software testing [7]. Because of the importance of CAs, quite a bit of research on the development of algorithms and effective methods to build them has been carried out to date.
Section II of this paper outlines the most significant methods and algorithms reported in the literature for the construction of CAs. Section III presents in detail the algorithms based on metaheuristics or hybridization of these, reported as having the best results to date. Section IV forecasts several upcoming trends for building CAs, and finally Section V brings together the conclusions.
II. Methods and algorithms for building Covering Arrays
The methods that have been developed to date for building CAs can be classified into four main groups [6]: exact, algebraic, Greedy, and Metaheuristic-based [7].
A. Exact methods
These are methods that enable the building of optimal CAs, but they are only practical for building small covering arrays [6]. In 2002, Meagher [8] presented a proposal for generating nonisomorphic CAs using a backtracking algorithm that builds each row of the CA recursively and independently. The algorithm builds all the possible CAs of a specific size but only works with binary alphabet [8]. EXACT (EXhaustive seArch of Combinatorial Test suites) proposed in 2006, enables the generation of Mixed Covering Arrays (MCA, arrays that have a different alphabet in their columns), reducing the search space to avoid exploring isomorphic arrays. It uses backtracking techniques to return again to the search process when it stagnates in the process of building the MCA [4]. In this proposal, the computing time increases significantly when the number of rows (N) of the CA is close to optimal. In addition, it does not find the solution for certain configurations. In 2009 [9], an algorithm for building CAs was presented with a backtracking technique, which creates the CA with a lexicographical order of rows and columns to avoid searching symmetrical arrays. The proposed algorithm was able to match the best solutions found by EXACT for small binary CAs and took less time. It also reported better CAs than those obtained with IPOG-F. The algorithm is limited to binary alphabet and strength 3<= t <= 5. In 2006, a proposal for building CAs was made using four constraint programming models such as SAT (propositional satisfiability problem). The proposed models are able to match existing boundaries and find new optimal values for problems of relatively moderate size. However, when the complexity of the CA to be built increases, either in terms of alphabet or strength, performance declines [10]; in the same vein, in 2008, Lopez-Escogido et al. [11] created CAs based on SAT. The main contribution of this proposal focuses on an efficient solver of non-CNF (non-conjunctive normal form) SAT that uses local search and is able to match or even improve some results generated by other approaches previously reported. However, the algorithm only works with strength t = 2 [11]. Torres-Jimenez et al. in 2015 [12] proposed a direct method to create optimal CAs of strength 2 based on binomial coefficients and in an algorithm based on branching and bound that links the results of the coefficients, making it possible to obtain CAs with large numbers of columns. The algorithm was compared with IPOG [13], one of the best greedy algorithms for building CAs, and performed better for small values of k, but as k increases, IPOG gives better results. The experiments were limited in the sense that IPOG only works with strength t <= 6, while the proposed algorithm works with higher strengths of t >=7.
B. Algebraic methods
The algorithms based on algebraic methods build CAs in polynomial time using predefined rules. The construction of the CAs directly uses some mathematical functions or other algebraic procedures [7]. Algebraic methods are applicable for very specific cases and offer efficient constructions in terms of time; however, currently, it is difficult to generate accurate results in a wide range of input values [14, 15]. For example, in the case of strength 2 and alphabet 2, in 1973 two algorithms were proposed that create optimal CAs, the first proposal by Katona [16] and the second by Kleitman and Spencer [17]. Chateauneuf et al. in 1999 [18] proposed an algorithm to create CAs of strength three using group actions on symbols/ alphabets, and then in 2005, Meagher and Stevens [19] adapted this method to create CAs of strength 2 using starter vectors that are rotated and translated to obtain the CA. Hartman in 2005 [20] proposed a method of squaring the number of columns of a CA using an orthogonal array as an intermediate tool. Colbourn et al. in 2006 [21] proposed a method for multiplying two CAs of strength 2 resulting in a new CA with the product of the original columns and the sum of the original rows. Finally, Colbourn in 2010 [22] proposed building CAs based on cyclotomic matrices.
C. Greedy methods
Greedy algorithms-based methods methods have been found to be relatively more efficient and faster Metaheuristic algorithms for building Covering Arrays: A review in terms of execution time. They have also been accurate for a wide variety of inputs. However, the CAs generated are not always the smallest compared to the CAs generated by other methods [14]. Greedy proposals include Density Deterministic Algorithm (DDA) proposed by Bryce and Colbourn in 2007 [23] that creates CAs of strength 2 a row at a time. In 1998 [24], Lei and Tai proposed the In-Parameter-Order (IPO) algorithm extending the array in both rows and columns, (i.e., it starts off with a CA of a number k columns and obtains one of k + 1 columns). This IPO algorithm is then generalized for strengths of greater than 2 in IPOG in 2007 [13], which is then improved in IPOG-F in 2008 [25]. Also in 2012, Gargantini Calvagna [26] extended the ideas of IPO to build MCAs of any strength.
D. Metaheuristic-based methods
Metaheuristic-based algorithms are computationally intensive and have provided the most accurate and competitive results to date. They have managed to generate CAs of the smallest size known (optimal) at a significant cost in run-time [14, 27]. Among the most important algorithms for building CAs are:
III. Algorithms based on metaheuristics
A. Simulated annealing
Simulated Annealing (SA) [36] is a general purpose stochastic optimization technique based on the steps for annealing of metals, steps employed in the industry to obtain materials that are more resilient and possess better qualities. The method starts with a heating process that basically consists of melting the material at a high temperature until it reaches its liquid state. At this point, the atoms significantly increase their mobility within the structure of the material. A cooling process then begins when the temperature is gradually lowered in steps, until the atoms are set properly before completely losing their mobility and thus achieving thermal equilibrium. When the process is complete, it is possible to achieve a highly regular and stable structure. Studies have shown that with sharp temperature drops or not waiting long enough at each stage, the resulting structure is not highly stable.
In 2003, Cohen et al. [37] applied the metaheuristic SA in the building of CAs. This proposal begins by randomly choosing an initial feasible solution S, corresponding to an array N x k with randomly chosen symbols of the specification of the CA desired. Using a sequence of trials, it randomly selects a cell from the array and the symbol is changed for a new one. If the transformation results in a feasible solution S', where the cost c(S') is less than or equal to the cost of c(S), then it is accepted as the new and current feasible solution. Otherwise, if the result is a more expensive feasible solution, S' is accepted with a probability e-(c(s))-c(s))/τ, where T is the control temperature of the simulation. Having the possibility of choosing a solution that is worse than the current one allows the algorithm to escape from the local optima. The temperature is decreased in small steps to achieve system equilibrium. This is done by adjusting T in each iteration to a value αT where α is a real number less than one. The algorithm stops when the objective function has a cost of zero, which means it has a CA. The algorithm also stops when the cost of the current solution does not change after a certain number of tests. The results of this research indicate that the SA makes it possible to build much smaller CAs than the algebraic methods. It fails, however, in bigger problems, especially when strength t is equal to or greater than 3.
In 2008, Cohen [38] made certain modifications to the original proposal, including a refinement to the Simulated Annealing algorithm that made it possible to find test cases faster, and include algebraic constructions that made it possible to build much smaller test cases. It also found new dimensions for some CAs of strength three. This hybrid approach is called Augmented Annealing.
In 2010, Torres-Jimenez and Rodriguez-Tello [39] presented a new implementation of the SA algorithm to build binary CAs of variable strength up to t = 5, which integrates three important characteristics that determine its performance. First, it incorporates an efficient heuristic to generate initial solutions of good quality; second, the design of a composite neighborhood function that allows the search to reduce rapidly the total cost of the candidate solutions, while avoiding falling into local minima; third, a cooling schedule that effectively allows the algorithm to converge much faster while generating solutions of quality. The algorithm was compared with the Deterministic Density Algorithm (DDA), Tabu Search, and IPOG-F algorithms [25]. The results showed that SA found new upper bounds and matched other previously known solutions from the references selected.
In 2012, Torres-Jimenez and Rodriguez-Tello [40] presented an improvement in the implementation of the SA algorithm called ISA, to build CA of strength t ϵ {3 -6} on a binary alphabet. The algorithm integrates two key characteristics that determine its performance: an efficient heuristic that generates good quality initial solutions that contain a balanced number of symbols in each column, and a carefully designed neighborhood function that allows a rapid search and reduces the cost of candidate solutions, avoiding falling into local minima. The performance of ISA was evaluated through extensive experimentation on a set of known reference cases, including 127 binary CAs of strength 3 to 6, and compared with various state of the art algorithms, among which were SA, a Greedy method, and TS. The computational results showed that the ISA algorithm has the advantage of producing smaller CAs than the other methods, at a moderate computational cost without major fluctuations in its average yield.
In 2012, Rodriguez-Cristerna and Torres-Jimenez [41] presented a hybrid approach called SA-VNS for building mixed covering arrays, (MCA, CAs with different possible values in columns) based on Simulated Annealing and a variable neighborhood search function (VNS). The solutions obtained by the hybrid algorithm SA-VNS were compared with other algorithms, including IPOG [13], IPOG-F and MiTS [42], managing to match 12 of the best known solutions and improving on six of these. The time required by SA-VNS is longer than the time needed for the algorithms mentioned above, but the improved results justify the extra time. In 2015, Rodriguez-Cristerna and Torres-Jimenez [43] presented the SAVNS algorithm as an improvement to the proposed SA-VNS. Among the main features of this new version of the algorithm are a mechanism for changing the size of the neighborhood in a range according to accepted movements, a mechanism for increasing the temperature and decreasing the probabilities of premature convergence, and a Metaheuristic algorithms for building Covering Arrays: A review probabilistic mixture of two neighborhood functions that operate as a local search, thus diversifying the search strategy. The algorithm was subjected to a tuning process that enabled the best configuration of the algorithm parameters to be established. The results from performance tests between SAVNS and other algorithms such as IPOG-F, MiTS, SA, TS and SA-VNS indicated that, based on nine cases or instances as benchmark, SAVNS managed to improve five instances of the best known algorithms solutions, mentioned above, with which it was compared.
In 2016, Torres-Jimenez [44] presented a system based on ISA [40] algorithm that equals or improves the size of the CAs reported by Colbourn [22] for strength 3, alphabet 3 and 105 ≤ N ≤ 223, thanks to two new neighborhood functions added. The proposal also defined a benchmark for 25 MCAs, and managed to find 579 new lower limits and match 13 previously known solutions. The algorithm is limited to a specified strength and alphabet.
B. Tabu search
Tabu Search (TS) is an approach to local search optimization that confronts different combinatorial optimization problems. This strategy, proposed in 1998 by Glover and Laguna [28], seeks to avoid falling into cycles and local minima, prohibiting or penalizing movements that have the solution in the next iteration, to point in the solution space previously visited, hence the term tabu. The basic idea of TS is to carry out a local search avoiding falling into a local minimum by choosing movements that do not improve the solution, with the assumption that a chosen bad strategy can give more information than a random good one. To avoid returning to past solutions and become stuck within cycles, a temporary memory is used, called tabu list, which stores the recent search history.
In 2004, Nurmela [45] used TS to find CAs. The algorithm starts with a randomly generated matrix M of size N x k, where the rows correspond to the CA alphabet. The cost of the matrix is defined by the number of missing combinations. A missing combination is then selected randomly. It is verified that rows require only a single element to be changed in order for the row to cover the selected combination. These changes are the movements of the current neighbor. The cost is calculated according to each movement of the neighbor and the movement that generates the lowest cost is selected, as long as it is not tabu (i.e., on the tabu list). If there is more than one movement with the same cost, one of the movements is selected at random. The process is repeated until the cost of the matrix M is zero or the maximum number of movements is reached. The results showed that the implementation improved some of the best previously known solutions. However, a major drawback of this algorithm is that it consumes considerably more computation time than other algorithms. Furthermore, in certain cases, it finished up taking several months to resolve the different test instances.
In 2009, Walker and Colbourn [46] used the tabu search algorithm to generate CAs from the permutation of vectors and mathematical objects, known as Covering Perfect Hash Families (CPHF). This representation of a CA is able to efficiently find smaller arrays for greater strengths t. It also enabled searches for t ≥ 5.
In 2010, González-Hernández et al. [47] presented an approach based on tabu search referred to as TSA for building Mixed Covering Arrays (MCA) of variable strength. The main features of this approach lie in the following aspects: first, the algorithm selects from a set of predefined neighborhood functions, where each is assigned a probability of being selected to create a new neighbor; secondly, it has an efficient calculation of the objective function to determine the best probability of selection for each neighborhood function; and thirdly, it has a new initialization function. Since TS performance depends on the values of the assigned probabilities, a tuning process was carried out on the configurations of these probabilities. The configuration used by TSA enabled the generation of MCAs of smaller size and in less time. TSA improved the size of the MCAs compared to IPOG-F, and found the optimal solution in 15 instances out of the 18 that make up the complete set. These instances range from an alphabet of 2 to 11, the number of columns from 2 to 20, and the strength from 2 to 6.
In 2013, González-Hernández [42] presented a combinatorial optimization algorithm for the construction of MCAs of variable strength called Mixed Tabu Search (MiTS), which uses the strategy metaheuristic of tabu search, and its main characteristic is the mixture of different neighborhood functions, each with a certain probability of being selected. Other important features included in the design of MiTS are the size of the tabu list used and the initialization function for creating the initial solution.
For each of these aspects, three different alternatives were proposed. Regarding the initialization functions, three different alternatives were incorporated into the algorithm: random, using the Hamming distance, and through a subset of t columns. The experimental results indicated that MiTS was able to establish 91 new optimal dimensions and matched 36 of the best cases reported in the literature, of which 31 were already optimal, so they were not susceptible to improvement.
In 2015, González-Hernández [48] developed a methodology that uses MiTS to build smaller MCAs than the best known, with uniform strength for values of t ϵ{2 -6}. The proposed methodology employs a tuning process that uses statistical tests to identify the values that significantly affect the performance of MiTS. To verify the efficiency of the proposed methodology, the performance of MiTS was compared and statistically analyzed against a robust set selection that included the best dimensions or limits of MCAs with strength t ϵ{2 -6} that have been reported to date for SA and DDA algorithms, among others. The methodology based on MiTS showed that there were significant differences between the solutions obtained and the best limits previously reported.
C. Genetic algorithms
A Genetic Algorithm (GA) is an adaptive method used to solve search and optimization problems. It is based on the process of biological evolution and uses the analogy of survival of the fittest individuals [49]. It begins with an initial population, which evolves through generations represented by iterations. In every generation, individuals are evaluated by a fitness function and in each generation the best individuals of the population survive. The next generations are generated by applying successively genetic operators such as selection, crossover, mutation and replacement. If the stop condition is met and a solution has not been found, the option is to mutate the population en masse.
In 2001, Stardom [50] presented results from comparing the optimization algorithms SA, TS and GA for building CAs. The three approaches were able to find new dimensions. However, genetic algorithms were not effective in finding CAs of quality. It took longer not only to execute movements but also to find a good CA. TS was the algorithm that yielded the best results.
In 2010, Rodriguez-Tello and Torres-Jimenez [51] presented a memetic algorithm (genetic algorithm that includes knowledge of the problem to find better solutions through a local optimizer) to find optimal solutions for building binary CAs of strength t = 3, which incorporated important features such as including an efficient heuristic to generate an initial population of good quality, and a local search operator based on the tuning of the SA algorithm. The computational results, compared with others in the literature among which are IPOG-F and TS, showed that the proposed algorithm improved in nine cases the best known solutions and matched the other results.
In 2016, Sabharwal et al. [52] presented G-PWiseGen, a general proposal of an existing open source tool called PWiseGen, which is used for generating test cases of strength 2. The main drawback of PWiseGen is that it requires to know in advance the size N of the test case as input. G-PWiseGen generates CAs for strength t ≥ 2, and on incorporating a binary search algorithm it is possible to set lower and upper limits for the size of the CA, eliminating the need to know N. G-PWiseGen was compared with other open source tools to generate CAs, such as ACTS, Jenny, TVG and CASA. The results showed that G-PWiseGen takes much longer to generate CAs with respect to the other propositions, due to the complexity in the crossover and mutation operations when the strength t is increased. Nevertheless, the sizes of the CAs generated compensate for the time spent on building them.
D. Ant colony
The Ant Colony algorithm (ACA), proposed in 1999 by Dorigo [53], is based on the structured behavior of ant colonies when looking for food. In this approach, each path from a starting point to an end point is associated with a candidate solution for a given problem. When an ant reaches the end point, the amount of pheromone deposited on each edge (vertex) of the path followed by the ant is proportional to the quality of the corresponding candidate solution. When an ant has to choose between the different edges at a given point (node), the edge with the greatest amount of pheromone is chosen with highest probability. As a result, the ants eventually converge to the shortest path.
In 2004, Shiba [54] presented a test generator algorithm based on genetic algorithms and ACA, and compared them with other algorithms including SA, IPO and The Automatic Efficient Test Generator (AETG) [55] that uses greedy strategy. The results for strength t ϵ{2 -3} showed a good performance at a general level with respect to the size of the test cases (N value in a CA) and the amount of time required for this. However, the genetic algorithm results were not always optimal. The results obtained by this algorithm were better than those generated by the GA.
In 2009, Chen [56] adapted the ACA algorithm to build a test set prioritized for the interaction of pairs, a CA and an MCA of strength t = 2. Specifically, he proposed four algorithms for generating tests based on ACA, looking for a more effective implementation. Although the results were competitive, their performance could not be generalized for instances with different characteristics.
E. Particle swarm optimization
The Particle Swarm Optimization algorithm (PSO) proposed in 1995 by Kennedy [33] is a popular optimization method. PSO attempts to optimize a problem starting with the handling of a certain number of candidate solutions. Each solution is represented by a particle that works in a search space to find a better position or solution to the problem. The population as a whole is known as a swarm. As such, each particle has a random position and updates its position iteratively in the hope of finding better solutions. Each particle also maintains essential information about its movements.
Applied to building CAs, a particle would usually represent a test case. Each particle is associated with a weighting factor that represents the number of interactions covered by the test case. When the evaluation of all particles finishes, those with the heaviest weighting will be chosen to be in the test sets.
In 2011, Ahmed and Kamal [57] developed a new strategy for generating test data pairs based on PSO, called Pairwise Particle Swarm based Test Generator (PPSTG). The study evaluated the performance of this proposal in terms of the size of the tests generated against other strategies and tools. In a first stage, PPSTG was compared with the results published in the literature for the GA, ACA, AETG and IPO algorithms [24], a Greedy algorithm. PPSTG generated test sets with satisfactory results in most experiments. However, GA and ACA generated slightly better sizes than PPSTG, which performed better than AETG. SA generated the most optimal results.
In 2011, Ahmed and Kamal [58] presented VS Particle Swarm Test Generator (VS-PSTG) to generate test cases in interactions of variable strength (VS). VSPSTG adopts PSO to ensure the optimal size reduction of the tests. Results in comparison with other strategies and configurations were seen to be competitive. An empirical case study was conducted on a non-trivial software system to show their applicability and determine the efficiency in generating test cases, with promising results.
In 2012, Ahmed et al. [59] demonstrated the efficiency of Particle Swarm-based t-way Test Generator (PSTG), a strategy for generating uniform CAs of variable strength, which copes with high interaction strengths of up to t = 6. PSTG is computationally lighter compared with other optimization methods due to the simplicity in the structure of the PSO algorithm on which it is based, and also outperforms other strategies in relation to sizes generated for the CA.
In 2015, Mahmoud and Ahmed [60] presented a strategy for building CAs using fuzzy logic to tune the heuristic parameters used by the PSO algorithm. The algorithm was tested with different proposals including SA and Hill Climbing. The results showed a significant improvement in terms of the size of the AC generated. Nevertheless, the diffuse mechanism called for additional computational requirements. Consequently, the strategy is comparatively slow at generating CAs of strength t > 4.
F. Harmony search
The Harmony Search algorithm (HS), proposed in 2001 by Zong Woo Geem and Kang Seo Lee [34], simulates the process of musical improvisation to find a perfect state of harmony. This harmony in music is analogous to finding an optimal in an optimization process. A musician will always try to produce a musical piece with perfect harmony. An optimal solution in an optimization problem must always be the best available solution to the problem under given objectives and certain restrictions. Both processes try to generate the best, or optimal [61].
In 2012, Rahman et al. [62] proposed and evaluated a strategy called Pairwise Harmony Search algorithmbased Strategy (PHSS) for generating test data in pairs. PHSS was evaluated in two parts. In the first part, a system configuration with 10 input parameters of v values was taken, where v ranged from 3 to 10. Another system configuration with p input parameters of 2 values was then taken, where p ranged from 3 to 15. The aim was to examine how PHSS behaved in relation to the variation of v and p. The results showed that its performance was not affected by the increasing number of v and p. In addition, in most cases the algorithm generated smaller test set sizes than other strategies, such as PPSTG, IPOG, TConfig, Jenny, and TVG, among others. In a second part, other system configurations were generated in order to compare the performance of PHSS against other representative strategies from the literature, such as SA, GA, and ACA. The PHSS results were competitive.
In 2012, Rahman et al. [62] designed, implemented, and evaluated an algorithm based on HS for variable strength called Harmony Search Strategy (HSS), which consists of two main algorithms. The first is an interaction generating algorithm that generates parameters, tuples and interaction values based on a specified strength, as well as on a list of constraints. The second is an algorithm for generating test cases in which harmony memory size, harmony memory consideration rate, tone adjustment rate, and stopping criteria are specified. The results of the algorithm were evaluated in two parts: in an initial part, the performance of HSS was evaluated in comparison with other strategies of variable strength, including VS-PSTG, ACS, SA, and IPOG. Depending on the strength, parameters and defined values, HSS generated the most optimal results for very high strengths because it is able to handle interaction strengths of up to t = 15. HSS outperformed other algorithms such as ACS and SA that generate test cases with interaction strength t ≤ 3 and VS-PSTG that generates test cases with interaction strength t ≤ 6. However, SA generated the most optimal results with low values of interaction t ≤ 3. HSS, VS-PSTG, and ACS obtained results equal or close to those of SA. IPOG was unable to handle strengths above t = 6. In a second part, HSS was compared with other strategies that handle restrictions, such as SA_SAT, PICT, TestCover, and mAETG_SAT.
However, these last two proposals despite being able to handle restrictions, were unsuccessful generating tests of varying strength. Therefore, they were not considered in the variable strength experiments. PICT reported the worst results. Finally, the results obtained by HSS were competitive with those produced by SA_SAT, since in most cases it was able to match the results, and only in some configurations it managed to surpass them.
In 2015, Bao et al. [63] presented the Improved Harmony Search (IHS) algorithm, a proposal that seeks to improve the speed of convergence of the standard HS algorithm. IHS uses a Greedy algorithm to generate an optimal set of initial solutions for initializing the harmony memory. To prevent the algorithm falling into local optima, the values of HMCR and PAR were dynamically adjusted. The results of the experiments showed that the size of the test cases generated by IHS is smaller than those generated by HS. It was further demonstrated that when the strength t is small, the runtime of IHS is very similar to that of HS. However, as t increases, the runtime of IHS significantly decreases compared to HS. On comparing IHS with other smart algorithms such as GA, ACA and SA, it could be seen that in most of the experiments the sizes of the IHS test cases were the most optimal.
IV. Trends
Currently, reports indicate that Simulated Annealing is one of the most successful metaheuristics in building CAs and MCAs regardless of strength, alphabet and number of columns. In this sense, it is considered that in the coming years, simulated annealing will continue to be studied and hybridized with various techniques (metaheuristic or otherwise) to find optimal or near optimal CAs.
Additionally, the use of different techniques to handle variable neighborhood or local searches with different neighborhood schemes has reported good results. Therefore, the authors believe that hyper-heuristic [64] and Multiple Offspring Sampling schemes [65], which use different local optimization schemes at the same time may be the future in building CAs and MCAs of variable strength and of different alphabets.
Given that day by day the complexity of the tasks that CAs use increases, as well as the required alphabets (v), numbers of columns (k), and levels of interaction (t), it is necessary for the academic and scientific community in this area to work on efficient ways to parallelize the use of metaheuristics that build CAs, and transfer them to different application areas (e.g., software and hardware testing, security, cryptography, etc.) as soon as possible, to offset the cost of building them.
Building covering arrays for strengths greater than 6 and hundreds of variables, which can be used among other things for the detection of Trojan horses in hardware [66], is one of the most recent application areas for building CAs using metaheuristics.
V. Conclusions
A method for building covering arrays is relevant if it finds an appropriate balance between the time for building it and the quality of array desired, the latter measured in the number of rows (N value) of the CA. If there is no time available for building the covering array test cases, using a greedy method is recommended. If time is available, the meta-heuristic methods are more suitable.
Although algebraic methods often provide good results for building covering arrays, they are applicable only to very specific and generally small cases. If they are used to find large CAs, a long run time and more computational resources are required. Greedy methods are more flexible than algebraic methods; however, they rarely obtain optimal covering arrays.
Recent advances in exact methods, specifically in the use of binomial coefficients and branching and pruning, establish an efficient strategy for building CAs of strength 2 and indicate a promising research path in the use of trinomial coefficients for obtaining CAs of strength 3.
Metaheuristic-based methods are the most recently used and generate better results in the construction of covering arrays. However, they require a lot of computing time. The Harmony search metaheuristic has been one of the least explored algorithms for building covering arrays, opening up the possibility for further research. The most successful metaheuristic method reported to date for the building of CAs is Simulated Annealing. The main reasons for this are its ability to escape from local optima thanks to the conditional acceptance of movements that do not necessarily improve the current solution, and, because it is not a population algorithm, its ability to evolve quickly to better regions of the search space enabling a mixture of different neighborhood functions.
References
[1] S. Maity, "Software Testing with Budget Constraints," in Information Technology: New Generations (ITNG), 2012 Ninth International Conference on, Apr. 2012, pp. 258-262. DOI: http://dx.doi.org/10.1109/itng.2012.44.
[2] G. J. Myers, C. Sandler, and T. Badgett, The art of software testing, 3rd edition. Hoboken, NJ, USA: John Wiley & Sons, Jan. 2012. DOI: http://dx.doi.org/10.1002/9781119202486.
[3] N. Changhai and H. Leung, "A Survey of Combinatorial Testing," ACM Computing Surveys, vol. 43, pp. 1-11, 2011. DOI: http://dx.doi.org/10.1145/1883612.1883618.
[4] J. Yan and J. Zhang, "Backtracking Algorithms and Search Heuristics to Generate Test Suites for Combinatorial Testing," 30th Annual International Computer Software and Applications Conference (COMPSAC'06), Chicago, IL, 2006, pp. 385-394. DOI: http://dx.doi.org/10.1109/COMPSAC.2006.33.
[5] H. Ávila George, J. T. Jiménez, and V. H. García, Verificación de Covering Arrays: Lambert Academic Publishing, 2010.
[6] J. Torres-Jimenez and I. Izquierdo-Márquez, "Survey of Covering Arrays," in Symbolic and Numeric Algorithms for Scientific Computing (SYNASC), 2013 15th International Symposium on, Sep. 2013, pp. 20-27. DOI: http://dx.doi.org/10.1109/synasc.2013.10.
[7] H. Ávila George, "Constructing Covering Arrays using Parallel Computing and Grid Computing," Ph.D. dissertation, Departamento de Sistemas Informáticos y Computación, Universitad Politécnica de Valencia, Valencia, Spain, 2012. DOI: http://dx.doi.org/10.4995/thesis/10251/17027.
[8] K. Meagher, "Non-Isomorphic Generation of Covering Arrays," University of Regina, Tech. Rep., 2002.
[9] J. Bracho-Rios, J. Torres-Jimenez, and E. Rodriguez-Tello, "A New Backtracking Algorithm for Constructing Binary Covering Arrays of Variable Strength," in MICAI 2009: Advances in Artificial Intelligence. vol. 5845, A. Aguirre, et al., Eds., ed: Springer Berlin Heidelberg, 2009, pp. 397-407. DOI: http://dx.doi.org/10.1007/978-3-642-05258-3_35.
[10] B. Hnich, S. D. Prestwich, E. Selensky, and B. M. Smith, "Constraint Models for the Covering Test Problem," Constraints, vol. 11 (2-3), pp. 199-219, Jul. 2006. DOI: http://dx.doi.org/10.1007/s10601-006-7094-9.
[11] D. Lopez-Escogido, J. Torres-Jimenez, E. Rodriguez-Tello, and N. Rangel-Valdez, "Strength Two Covering Arrays Construction Using a SAT Representation," in MICAI 2008: Advances in Artificial Intelligence. vol. 5317, A. Gelbukh and E. Morales, Eds., ed: Springer Berlin Heidelberg, 2008, pp. 44-53. DOI: http://dx.doi.org/10.1007/978-3-540-88636-5_4.
[12] J. Torres-Jimenez, I. Izquierdo-Marquez, A.Gonzalez-Gomez, and H. Ávila-George, "A Branch & Bound Algorithm to Derive a Direct Construction for Binary Covering Arrays," in G. Sidorov and S. Galicia-Haro (Eds.), Advances in Artificial Intelligence and Soft Computing. vol. 9413, pp. 158-177, Springer International Publishing, 2015. DOI: http://dx.doi.org/10.1007/978-3-319-27060-9_13.
[13] Y. Lei, R. Kacker, D. R. Kuhn, V. Okun, and J. Lawrence, "IPOG: A General Strategy for T-Way Software Testing," presented at the Proceedings of the 14th Annual IEEE International Conference and Workshops on the Engineering of Computer-Based Systems, 2007. DOI: http://dx.doi.org/10.1109/ecbs.2007.47.
[14] R. C. Turban, "Algorithms for covering arrays," Ph.D. dissertation, Arizona State University, 2006.
[15] J. Zhang, Z. Zhang, and F. Ma, Automatic Generation of Combinatorial Test Data: Springer Publishing Company, Incorporated, 2014. DOI: http://dx.doi.org/10.1007/9783-662-43429-1.
[16] G. O. H. Katona, "Two applications (for search theory and truth functions) of Sperner type theorems," Periodica Mathematica Hungarica, vol. 3 (1-2), pp. 19-26, Mar. 1973. DOI: http://dx.doi.org/10.1007/BF02018457.
[17] D. J. Kleitman, and J. Spencer, "Families of k-independent sets," Discrete Mathematics, vol. 6 (3), pp. 255-262, 1973. DOI: http://dx.doi.org/10.1016/0012-365X(73)90098-8.
[18] M. A. Chateauneuf, C. J. Colbourn, and D. L. Kreher, "Covering Arrays of Strength Three," Des Codes and Cryptogr, vol. 16 (3), pp. 235-242, May. 1999. DOI: http://dx.doi.org/10.1023/A:1008379710317.
[19] K. Meagher and B. Stevens, "Group construction of covering arrays," Journal of Combinatorial Designs, vol. 13 (1), pp. 70-77, Jan. 2005. DOI: http://dx.doi.org/10.1002/jcd.20035.
[20] A. Hartman, "Software and Hardware Testing Using Combinatorial Covering Suites," in M. Golumbic and I.-A. Hartman (Eds.), Graph Theory, Combinatorics and Algorithms. vol. 34, pp. 237-266, ed: Springer US, 2005. DOI: http://dx.doi.org/10.1007/0-387-25036-0_10.
[21] C. J. Colbourn et al., "Products of mixed covering arrays of strength two," Journal of Combinatorial Designs, vol. 14 (2), pp. 124-138, Mar. 2006. DOI: http://dx.doi.org/10.1002/jcd.20065.
[22] C. Colbourn, "Covering arrays from cyclotomy," Des Codes and Cryptogr, vol. 55 (2-3), pp. 201-219, May. 2010. DOI: http://dx.doi.org/10.1007/s10623-009-9333-8.
[23] R. C. Bryce and C. J. Colbourn, "The density algorithm for pairwise interaction testing," Softw Test Verif Reliab, vol. 17 (3), pp. 159-182, Sep. 2007. DOI: http://dx.doi.org/10.1002/stvr.365.
[24] Y. Lei and K.-C. Tai, "In-Parameter-Order: A Test Generation Strategy for Pairwise Testing," presented at the The 3rd IEEE International Symposium on High-Assurance Systems Engineering, 1998. DOI: http://dx.doi.org/10.1109/HASE.1998.731623.
[25] M. Forbes et al., "Refining the in-parameterorder strategy for constructing covering arrays," Journal of Research of the National Institute of Standards and Technology, vol. 113 (5), pp. 287-297, Sep. 2008. DOI: http://dx.doi.org/10.6028/jres.113.022.
[26] A. Calvagna and A. Gargantini, "T-wise combinatorial interaction test suites construction based on coverage inheritance," Softw Test Verif Reliab, vol. 22 (7), pp. 507-526, Nov. 2012. DOI: http://dx.doi.org/10.1002/stvr.466.
[27] R. N. Kacker et al., "Combinatorial testing for software: An adaptation of design of experiments," Measurement, vol. 46 (9), pp. 3745-3752, Nov. 2013. DOI: http://dx.doi.org/10.1016/j.measurement.2013.02.021.
[28] F. Glover and M. Laguna, Tabu Search: Kluwer Academic Publishers, 1997. DOI: http://dx.doi.org/10.1007/978-1-4615-6089-0.
[29] M. Gendreau, "Recent Advances in Tabu Search," in Essays and Surveys in Metaheuristics. vol. 15, ed: Springer US, 2002, pp. 369-377. DOI: http://dx.doi.org/10.1007/978-1-46151507-4_16.
[30] M. Gendreau and J. Y. Potvin, Handbook of Metaheuristics: Springer US, 2010. DOI: http://dx.doi.org/10.1007/978-1-4419-1665-5.
[31] S. Luke. Essentials of Metaheuristics, 2nd ed. Lulu, 2013.
[32] M. Dorigo and T. Stützle, Ant Colony Optimization: Bradford Company, 2004.
[33] J. Kennedy and R. Eberhart, "Particle swarm optimization," in Neural Networks, 1995. Proc. IEEE Int. Conf. Neural Netw. on, Nov. 1995, pp. 1942-1948 vol.4. DOI: http://dx.doi.org/10.1109/icnn.1995.488968.
[34] Z. Geem et al., "A New Heuristic Optimization Algorithm: Harmony Search," SIMULATION, vol. 76, pp. 60-68, 2001. DOI: http://dx.doi.org/10.1177/003754970107600201.
[35] M. G. H. Omran and M. Mahdavi, "Globalbest harmony search," Applied Mathematics and Computation, vol. 198 (2), pp. 643-656, May. 2008. DOI: http://dx.doi.org/10.1016/j.amc.2007.09.004.
[36] S. Kirkpatrick and M. Vecchi, "Optimization by simmulated annealing," science, vol. 220, pp. 671-680, 1983. DOI: http://dx.doi.org/10.1126/science.220.4598.671.
[37] M. B. Cohen et al., "Constructing test suites for interaction testing," presented at the Proceedings of the 25th International Conference on Software Engineering, Portland, Oregon, 2003. DOI: http://dx.doi.org/10.1109/icse.2003.1201186.
[38] M. B. Cohen et al., "Constructing strength three covering arrays with augmented annealing," Discrete Mathematics, vol. 308 (13), pp. 2709-2722, Jul. 2008. DOI: http://dx.doi.org/10.1016/j.disc.2006.06.036.
[39] J. Torres-Jimenez and E. Rodriguez-Tello, "Simulated Annealing for constructing binary covering arrays of variable strength," in Evolutionary Computation (CEC), 2010 IEEE Congress on, 2010, pp. 1-8. DOI: http://dx.doi.org/10.1109/cec.2010.5586148.
[40] J. Torres-Jimenez and E. Rodriguez-Tello, "New bounds for binary covering arrays using simulated annealing," Information Sciences, vol. 185 (1), pp. 137-152, Feb. 2012. DOI: http://dx.doi.org/10.1016/j.ins.2011.09.020.
[41] A. Rodriguez-Cristerna and J. Torres-Jimenez, "A Simulated Annealing with Variable Neighborhood Search Approach to Construct Mixed Covering Arrays," Electronic Notes in Discrete Mathematics, vol. 39, pp. 249-256, Dec. 2012. DOI: http://dx.doi.org/10.1016/j.endm.2012.10.033.
[42] A. L. González Hernández, "Un Algoritmo de Optimizacion Combinatoria para la Construccion de Covering Arrays Mixtos de Fuerza Variable," PhD. dissertation, Laboratorio de Tecnologías de la Información, Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional, 2013.
[43] A. Rodriguez-Cristerna et al., "Construction of Mixed Covering Arrays Using a Combination of Simulated Annealing and Variable Neighborhood Search," Electronic Notes in Discrete Mathematics, vol. 47, pp. 109-116, Feb. 2015. DOI: http://dx.doi.org/10.1016/j.endm.2014.11.015.
[44] J. Torres-Jimenez et al., "A two-stage algorithm for combinatorial testing," Optimization Letters, pp. 1-13, 2016. DOI: http://dx.doi.org/10.1007/s11590-016-1012-x.
[45] K. J. Nurmela, "Upper bounds for covering arrays by tabu search," Discrete Applied Mathematics, vol. 138 (1-2), pp. 143-152, Mar. 2004. DOI: http://dx.doi.org/10.1016/S0166218X(03)00291-9.
[46] R. A. Walker Ii and C. J. Colbourn, "Tabu search for covering arrays using permutation vectors," Journal of Statistical Planning and Inference, vol. 139 (1), pp. 69-80, Jan. 2009. DOI: http://dx.doi.org/10.1016/j.jspi.2008.05.020.
[47] L. Gonzalez-Hernandez et al., "Construction of Mixed Covering Arrays of Variable Strength Using a Tabu Search Approach," in Combinatorial Optimization and Applications. vol. 6508, W. Wu and O. Daescu, Eds., ed: Springer Berlin Heidelberg, 2010, pp. 51-64. DOI: http://dx.doi.org/10.1007/978-3-64217458-2_6.
[48] L. Gonzalez-Hernandez, "New bounds for mixed covering arrays in t-way testing with uniform strength," Information and Software Technology, vol. 59, pp. 17-32, Mar. 2015. DOI: http://dx.doi.org/10.1016/j.infsof.2014.10.009.
[49] X. Yu and M. Gen. Introduction to Evolutionary Algorithms. Springer London, 2010. DOI: http://dx.doi.org/10.1007/978-1-84996-129-5.
[50] J. Stardom, "Metaheuristics and the Search for Covering and Packing Arrays," M.S. thesis, Simon Fraser University, 2001.
[51] E. Rodriguez-Tello and J. Torres-Jimenez, "Memetic Algorithms for Constructing Binary Covering Arrays of Strength Three," in Artifical Evolution. vol. 5975, P. Collet, et al., Eds., ed: Springer Berlin Heidelberg, 2010, pp. 86-97. DOI: http://dx.doi.org/10.1007/978-3-64214156-0_8.
[52] S. Sabharwal et al., "Construction of t-way covering arrays using genetic algorithm," International Journal of System Assurance Engineering and Management, pp. 1-11, 2016. DOI: http://dx.doi.org/10.1007/s13198-0160430-6.
[53] M. Dorigo et al., "Ant system: optimization by a colony of cooperating agents," IEEE Trans. Syst., Man, Cybern. B, Cybern., vol. 26 (1), pp. 29-41, Feb. 1996. DOI: http://dx.doi.org/10.1109/3477.484436.
[54] T. Shiba et al., "Using artificial life techniques to generate test cases for combinatorial testing," in Computer Software and Applications Conference, 2004. COMPSAC 2004. Proceedings of the 28th Annual International, 2004, pp. 72-77 vol.1. DOI: http://dx.doi.org/10.1109/CMPSAC.2004.1342808.
[55] D. M. Cohen et al., "The Automatic Efficient Test Generator (AETG) system," in Software Reliability Engineering, 1994. Proceedings., 5th International Symposium on, 1994, pp. 303-309. DOI: http://dx.doi.org/10.1109/issre.1994.341392.
[56] X. Chen et al., "Building Prioritized Pairwise Interaction Test Suites with Ant Colony Optimization," in 9th International Conference on Quality Software, Jeju, 2009, pp. 347-352. DOI: http://dx.doi.org/10.1109/QSIC.2009.52.
[57] B. S. Ahmed et al., "The development of a particle swarm based optimization strategy for pairwise testing," Journal of Artificial Intelligence, vol. 4 (2), pp. 156-165, Feb. 2011. DOI: http://dx.doi.org/10.3923/jai.2011.156.165.
[58] B. S. Ahmed and K. Z. Zamli, "A variable strength interaction test suites generation strategy using Particle Swarm Optimization," Journal of Systems and Software, vol. 84 (12), pp. 2171-2185, Dec. 2011. DOI: http://dx.doi.org/10.1016/j.jss.2011.06.004.
[59] B. S. Ahmed et al., "Application of Particle Swarm Optimization to uniform and variable strength covering array construction," Applied Soft Computing, vol. 12 (4), pp. 1330-1347, Apr. 2012. DOI: http://dx.doi.org/10.1016/j.asoc.2011.11.029.
[60] T. Mahmoud and B. S. Ahmed, "An efficient strategy for covering array construction with fuzzy logic-based adaptive swarm optimization for software testing use," Expert Systems with Applications, vol. 42 (22), pp. 8753-8765, Dec. 2015. DOI: http://dx.doi.org/10.1016/j.eswa.2015.07.029.
[61] X.-S. Yang, "Harmony Search as a Metaheuristic Algorithm," in Music-Inspired Harmony Search Algorithm. vol. 191, ed: Springer Berlin Heidelberg, 2009, pp. 1-14. DOI: http://dx.doi.org/10.1007/978-3-642-00185-7_1.
[62] A. R. A. Alsewari and K. Z. Zamli, "A harmony search based pairwise sampling strategy for combinatorial testing," International Journal of the Physical Sciences, vol. 7, pp. 1062-1072, 2012. DOI: http://dx.doi.org/10.5897/IJPS11.1633.
[63] X. Bao et al., "Combinatorial Test Generation Using Improved Harmony Search Algorithm," International Journal of Hybrid Information Technology, vol. 8 (9), pp. 121-130, Sep. 2015. DOI: http://dx.doi.org/10.14257/ijhit.2015.8.9.13.
[64] E. K. Burke et al., "Hyper-heuristics: A survey of the state of the art," Journal of the Operational Research Society, vol. 64 (12), pp. 1695-1724, Dec. 2013. DOI: http://dx.doi.org/10.1057/jors.2013.71.
[65] A. LaTorre et al., "Multiple Offspring Sampling in Large Scale Global Optimization," in 2012 IEEE Congress on Evolutionary Computation, 2012, pp. 1-8. DOI: http://dx.doi.org/10.1109/CEC.2012.6256611.
[66] P. Kitsos et al., "Exciting FPGA cryptographic Trojans using combinatorial testing," in 2015 IEEE 26th International Symposium on Software Reliability Engineering (ISSRE), Nov. 2015, pp. 69-76. DOI: http://dx.doi.org/10.1109/issre.2015.7381800.