Didactic suitability criteria in a Lesson Study-based class

Abstract

This study seeks to identify the didactic suitability criteria used by a group of teachers in a training process of a class—design, implementation, and reflection/redesign—carried out under an experience of lesson study. The didactic suitability tool is used for qualitative analysis. It is concluded that the group of teachers implicitly uses some of the components and indicators of didactic suitability. In particular, the interactional and cognitive criteria are used in a more comprehensive way and, in a less detailed manner, the epistemic and emotional criteria. Furthermore, the means and ecological criteria are rarely used in the group’s reflection.

Keywords: lesson study, didactic suitability, teacher reflection

Critérios de idoneidade didática numa classe baseada no Lesson Study

Resumo

O objetivo deste trabalho é identificar os critérios de idoneidade didática usados por um grupo de professores num processo de instrução de uma classe — desenho, implementação e reflexão/redesenho — realizado no marco de uma experiência de estudo de classes. Utiliza-se a ferramenta idoneidade didática para a análise qualitativa. Conclui-se que o grupo de professores utiliza, de maneira implícita, alguns dos componentes e indicadores dos critérios de idoneidade didática. Em particular, utilizam-se de maneira mais completa os critérios interacional e cognitivo e, de forma menos detalhada, os critérios epistémico e emocional. Por outra parte, os critérios de meios e ecológico são pouco utilizados na reflexão do grupo.

Palavras-chave: estudo de classes, idoneidade didática, reflexão docente

Introducción1

Diversas tendencias sobre la formación de profesores dan cuenta de estudios acerca de la reflexión sobre la práctica docente como una estrategia clave para el desarrollo profesional y la mejora de la enseñanza (Brockbank & McGill, 2002; Dewey, 1989; Schön, 1992). En esta línea, Perrenoud (2004) argumenta que, para conseguir profesores reflexivos, es necesario que el profesor tenga un método de reflexión —que en general puede ser similar en diferentes asuntos— y, por otro lado, estructuras conceptuales específicas de cada disciplina que son necesarias para comprender, organizar y analizar informaciones sobre lo que reflexiona.

Tal como se afirma en Breda, Font y Pino-Fan (2018), desde la didáctica de las matemáticas han surgido diferentes propuestas que proporcionan marcos conceptuales relacionados con el desarrollo de la competencia reflexiva. Una de ellas es la metodología de estudio de clases (Fernández & Yoshida, 2004) y otra es la noción de idoneidad didáctica, propuesta en el marco del enfoque ontosemiótico (Font, Planas & Godino, 2010; Godino, Contreras & Font, 2006).

La metodología Lesson Study [EC, por su traducción: estudio de clases], es una actividad de investigación en el aula (Baldin, 2009; Burghes & Robinson, 2010; Ponte, Baptista, Velez & Costa, 2012; Yoshida, 2012) que fomenta el desarrollo de la competencia reflexiva durante la realización de la actividad docente. Por otro lado, el enfoque ontosemiótico de la cognición e instrucción matemática [EOS] ha desarrollado los criterios de idoneidad didáctica [CI] como una herramienta para estructurar la reflexión del profesor. En esta última perspectiva, dichos criterios pueden servir para guiar los procesos de enseñanza y aprendizaje de las matemáticas y para evaluar su implementación, sean estos propios o ajenos (Breda, Font & Lima, 2015; Breda et al., 2018).

Partiendo de la idea de que la reflexión del profesorado es clave para el desarrollo profesional y la mejora de la enseñanza y aprendizaje de las matemáticas, el objetivo de este trabajo es analizar cuáles son los criterios de idoneidad usados implícitamente por un grupo de profesores —maestros de primaria— en un proceso de instrucción de una clase —diseño, implementación y reflexión/rediseño— que se realiza en el marco de una experiencia de EC.

A continuación, se muestra el marco teórico: la metodología EC y los CI. Luego, se presenta la metodología cualitativa usada en la investigación para analizar los datos de un estudio de caso donde hay una experiencia de EC. Más adelante, se hace el análisis de los datos —se examina si las consideraciones de los profesores se pueden interpretar como evidencias de empleo implícito de algunos de los componentes e indicadores de los CI—. Finalmente, se hace una discusión sobre los resultados obtenidos a partir de los datos analizados.

Marco teórico

El enfoque EC. Uno de los países que más se destaca por su alto rendimiento y desempeño en matemáticas en las evaluaciones internacionales es Japón. Una característica de este país es el uso de la metodología EC para mejorar la enseñanza y aprendizaje de las matemáticas. Se trata de una metodología de trabajo docente, apoyada en actitudes investigativas y prácticas colaborativas de los profesores, cuyo objetivo es tanto la mejora de la práctica docente y del aprendizaje de los estudiantes, como el desarrollo profesional de los profesores (Huang & Shimizu, 2016).

Los EC se desarrollan en cuatro etapas (Hart, Alston & Murata, 2011; Yoshida, 2012):

1. Planificación de la clase: un grupo de profesores elige los temas a desarrollar; establece los objetivos para los aprendizajes y el desarrollo de los alumnos; elige el material didáctico; y reflexiona sobre posibles respuestas y el comportamiento de los estudiantes frente a las cuestiones propuestas.
2. Realización y observación de la clase: un profesor comparte su clase mientras los demás observan y registran el proceso de enseñanza y aprendizaje, para lo cual este profesor debe estar de acuerdo en que los demás puedan presenciar su clase en vivo. La participación de los alumnos es activa en cada etapa de resolución de las cuestiones propuestas, desde la comprensión del problema, el establecimiento de estrategias y análisis de la resolución, lo cual estimula el cuestionamiento y el descubrimiento de los estudiantes. Se trata de una etapa donde se da mucha importancia al proceso de resolución de problemas.
3. Reflexión conjunta sobre los datos registrados: después de la clase, los profesores —observados y observadores— se reúnen para evaluar el proceso de instrucción implementado.
4. Rediseño: a partir de las discusiones realizadas en la etapa anterior, el plan de clase es reestructurado considerando las aportaciones del grupo. Se aplica en otra clase y se inicia un nuevo ciclo.

Los CI. Los CI, propuestos en el marco teórico EOS, pretenden ser una respuesta parcial a la siguiente problemática: ¿qué criterios se deben utilizar para diseñar una secuencia de tareas que permita evaluar y desarrollar la competencia matemática de los alumnos? ¿Qué cambios se deben realizar en su rediseño para mejorar el desarrollo de esta competencia? Los CI pueden servir para guiar los procesos de enseñanza y aprendizaje de las matemáticas y para valorar sus implementaciones. En el EOS se consideran los siguientes CI (Font et al., 2010):

1. Idoneidad epistémica, para valorar si las matemáticas que están siendo enseñadas son “buenas matemáticas”.
2. Idoneidad cognitiva, para valorar, antes de iniciar el proceso de instrucción, si lo que se quiere enseñar está a una distancia razonable de aquello que los alumnos saben y, después del proceso, si los aprendizajes adquiridos están cerca de aquello que se pretendía enseñar.
3. Idoneidad interaccional, para valorar si las interacciones resuelven dudas y dificultades de los alumnos.
4. Idoneidad mediacional, para valorar la adecuación de los recursos materiales y temporales utilizados en el proceso de instrucción.
5. Idoneidad emocional, para valorar la implicación —intereses y motivaciones— de los alumnos durante el proceso de instrucción.
6. Idoneidad ecológica, para valorar la adecuación del proceso de instrucción al proyecto educativo del centro, a las directrices curriculares, y a las condiciones del entorno social y profesional.

La operatividad de los CI exige definir un conjunto de indicadores observables que permitan valorar el grado de idoneidad de cada uno de estos criterios. Por ejemplo, existe consenso de que es necesario implementar unas “buenas” matemáticas, pero es posible entender cosas muy diferentes por ello. Para algunos CI, los indicadores son relativamente fáciles de consensuar —por ejemplo, para el criterio de idoneidad de medios—; para otros, como es el caso de la idoneidad epistémica, es más difícil. En Breda y Lima (2016), Seckel (2016), Breda, Pino-Fan y Font (2017) y Breda et al. (2018) se aporta un sistema de indicadores que sirve de guía de análisis y valoración de la idoneidad didáctica, que está pensado para un proceso de instrucción en cualquier etapa educativa. En el Cuadro 1, se presentan los componentes e indicadores de los CI.

Cuadro 1

Componentes e indicadores de los CI

Componentes	Indicadores
Idoneidad epistémica
Errores	No se observan prácticas que se consideren incorrectas desde el punto de vista matemático.
Ambigüedades	No se observan ambigüedades que puedan llevar a la confusión a los alumnos: definiciones y procedimientos clara y correctamente enunciados, adaptados al nivel educativo al que se dirigen; adecuación de las explicaciones, comprobaciones, demostraciones al nivel educativo a que se dirigen, uso controlado de metáforas...
Riqueza de procesos	La secuencia de tareas contempla la realización de procesos relevantes en la actividad matemática —modelización, argumentación, resolución de problemas, conexiones…—.
Representatividad	Los significados parciales —definiciones, propiedades, procedimientos…— son una muestra representativa de la complejidad de la noción matemática que se quiere enseñar contemplada en el currículo. Los significados parciales —definiciones, propiedades, procedimientos....— son una muestra representativa de la complejidad de la noción matemática que se quiere enseñar. Para uno o varios significados parciales, muestra representativa de problemas. Para uno o varios significados parciales, uso de diferentes modos de expresión —verbal, gráfico, simbólico…—, tratamientos y conversiones entre los mismos.
Idoneidad cognitiva
Conocimientos previos —componentes similares a la idoneidad epistémica—	Los alumnos tienen los conocimientos previos necesarios para el estudio del tema —bien se han estudiado anteriormente o el profesor planifica su estudio—. Los significados pretendidos se pueden alcanzar —tienen una dificultad manejable— en sus diversos componentes.
Adaptación curricular a las diferencias individuales	Se incluyen actividades de ampliación y de refuerzo.
Aprendizaje	Los diversos modos de evaluación muestran la apropiación de los conocimientos / competencias pretendidas o implementadas.
Alta demanda cognitiva	Se activan procesos cognitivos relevantes —generalización, conexiones intra-matemáticas, cambios de representación, conjeturas…—. Promueve procesos metacognitivos.
Idoneidad interaccional
Interacción docente-discente	El profesor hace una presentación adecuada del tema —presentación clara y bien organizada, no habla demasiado rápido, enfatiza los conceptos clave del tema....—. Se reconocen y resuelven los conflictos de significado de los alumnos —se interpretan correctamente los silencios de los alumnos, sus expresiones faciales, sus preguntas, se hace un juego de preguntas y respuestas adecuado…—. Se busca llegar a consensos con base en el mejor argumento. Se usan diversos recursos retóricos y argumentativos para implicar y captar la atención de los alumnos. Se facilita la inclusión de los alumnos en la dinámica de la clase y no la exclusión.
Interacción entre discentes	Se favorece el diálogo y comunicación entre los estudiantes. Se favorece la inclusión en el grupo y se evita la exclusión.
Autonomía	Se contemplan momentos en los que los estudiantes asumen la responsabilidad del estudio —exploración, formulación y validación—.
Evaluación formativa	Observación sistemática del progreso cognitivo de los alumnos.
Idoneidad mediacional
Recursos materiales —manipulativos, calculadoras, computadoras—	Uso de materiales manipulativos e informáticos que permiten introducir buenas situaciones, lenguajes, procedimientos, argumentaciones adaptadas al significado pretendido. Las definiciones y propiedades son contextualizadas y motivadas usando situaciones y modelos concretos y visualizaciones.
Número de alumnos, horario y condiciones del aula	El número y la distribución de los alumnos permiten llevar a cabo la enseñanza pretendida. El horario del curso es apropiado —por ejemplo, no se imparten todas las sesiones a última hora—. El aula y la distribución de los alumnos es adecuada para el desarrollo del proceso instruccional pretendido.
Tiempo —de la enseñanza colectiva / tutoría, tiempo de aprendizaje—	Adecuación de los significados pretendidos /implementados al tiempo disponible —presencial y no presencial—. Inversión del tiempo en los contenidos más importantes o nucleares del tema. Inversión del tiempo en los contenidos que presentan más dificultad.
Idoneidad emocional
Intereses y necesidades	Selección de tareas de interés para los alumnos. Proposición de situaciones que permitan valorar la utilidad de las matemáticas en la vida cotidiana y profesional.
Actitudes	Promoción de la implicación en las actividades, la perseverancia, responsabilidad... Se favorece la argumentación en situaciones de igualdad; el argumento se valora en sí mismo y no por quien lo dice.
Emociones	Promoción de la autoestima, al evitar el rechazo, fobia o miedo a las matemáticas. Se resaltan las cualidades de estética y precisión de las matemáticas.
Idoneidad ecológica
Adaptación al currículo	Los contenidos, su implementación y evaluación se corresponden con las directrices curriculares.
Conexiones intra- e interdisciplinares	Los contenidos se relacionan con otros contenidos matemáticos —conexión de matemáticas avanzadas con las matemáticas del currículo y conexión entre diferentes contenidos matemáticos contemplados en el currículo— o bien con contenidos de otras disciplinas —contexto extra-matemático, bien con contenidos de otras asignaturas de la etapa educativa—.
Utilidad socio-laboral	Los contenidos son útiles para la inserción socio-laboral.
Innovación didáctica	Innovación basada en la investigación y la práctica reflexiva —introducción de nuevos contenidos, recursos tecnológicos, formas de evaluación, organización del aula…—.

Fuente: Breda, Font, Lima y Pereira (2018).

Tal como se muestra en la revisión de la literatura realizada en Breda et al. (2015), la noción de idoneidad didáctica ha tenido un impacto relevante en la formación de profesores en diferentes países (Mallart, Font & Malaspina, 2016; Pochulu, Font & Rodríguez, 2016; Seckel & Font, 2015). Dicho impacto está relacionado con la idea de que uno de los componentes del conocimiento didáctico-matemático del profesor es aquel que permite valorar y justificar la mejora de los procesos de enseñanza y aprendizaje de las matemáticas.

Metodología

En esta investigación, de carácter exploratorio y analítico-interpretativo, se realiza el análisis cualitativo de un video que presenta diferentes etapas —diseño, implementación, reflexión/rediseño— de una experimentación de un EC, con el propósito de examinar cuáles fueron los CI utilizados implícitamente por un profesor y sus colaboradores. Se trata de un estudio de caso (Ponte, 1994; Yin, 2001).

Después de una búsqueda de diferentes videos sobre EC en YouTube, se seleccionó este video por dos razones. La primera, fue el importante número de visualizaciones del video y, la segunda, porque en este video se puede observar el proceso de EC de forma completa, es decir, hay una fase de diseño, una de implementación, una de reflexión y una de rediseño de la clase.

Esencialmente, se buscó primero seleccionar consideraciones empleadas por el profesor y sus colegas para fundamentar la secuencia de tareas que se proponen en la clase. En segundo lugar, se analizó si estas consideraciones se pueden interpretar como evidencias de empleo implícito de algunos de los componentes e indicadores de los CI.

El video analizado está en español, es decir, ya viene con la traducción del japonés al español incorporada.

Análisis de una experiencia de EC

El video analizado trata de un proceso de instrucción llevado a cabo por el profesor Takao Seiyama [P] en una clase de segundo grado de la escuela primaria. La clase se enfoca en substraer de un número de tres dígitos un número de dos dígitos, de manera que el resultado sea un número de un dígito (imagen 1). Para eso, el profesor utiliza problemas de restas en los que hay que rellenar los espacios en blanco cuando solo se sabe el resultado. Ahora bien, la primera formulación que hace el profesor no es muy clara, ya que dice literalmente lo siguiente:

P: Con ese tipo de problema solo uno o dos dígitos están escondidos. No voy a esconder los dos números en el problema de restas. La respuesta está ahí. Los estudiantes tienen que averiguar la ecuación de resta que conduzca a esa respuesta. Pienso que será suficiente para atraer su atención en el problema. (Dgespetv, 2012)

Por lo que se observa en la implementación posterior, cuando dice dígitos se está refiriendo a números —minuendo y sustraendo—. A pesar que dice que no va esconder los dos números, esconde el minuendo y el sustraendo. Cuando dice ecuación de resta, se está refiriendo a las combinaciones de minuendo y sustraendo que dan el resultado suministrado.

Imagen 1. Tarea propuesta por el profesor P. Fuente: Dgespetv (2012).

Ahora bien, con independencia de la diferencia que se observa entre esta primera formulación del objetivo y la implementación posterior, podemos inferir que P está realizando una valoración positiva de determinados aspectos en la experiencia de EC prevista. En concreto, utiliza implícitamente el indicador selección de tareas de interés para los alumnos del componente intereses y necesidades del criterio de idoneidad emocional, ya que valora positivamente el hecho de elaborar una actividad que favorezca el interés de los alumnos. Además, esta motivación se conseguirá presentando una tarea de alta demanda cognitiva —otro componente de la idoneidad cognitiva—.

Además de la motivación, P también pretendía que los estudiantes encontraran ciertas reglas ocultas en las respuestas del problema. La primera regla era la de que dado un resultado y hallada una combinación de minuendo y sustraendo que dan dicho resultado, si el minuendo y el sustraendo se incrementan en una unidad, entonces se obtiene el mismo resultado. La segunda regla era que, para un valor de la diferencia x, hay un número x de combinaciones de minuendo y sustraendo posibles. Por ejemplo, hay tres combinaciones cuando la diferencia es tres (imagen 2), cinco combinaciones cuando la diferencia es cinco y así en adelante. Al descubrir estas reglas, pueden encontrar todas las combinaciones del minuendo y substraendo más rápidamente.

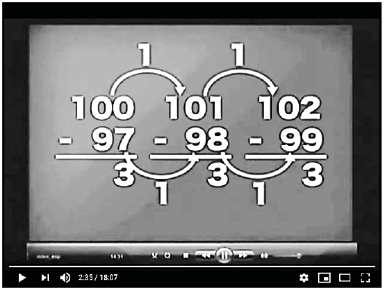
Imagen 2. Regla del problema. Fuente: Dgespetv (2012).

El supervisor de las clases [S], hace una visita a P en el momento en que él está planeando su clase. En este momento el profesor le pide su opinión.

P: Tú ves que la diferencia y el número de ecuaciones es el mismo. Yo creo que los estudiantes van a notar que hay algo aquí.

S: Sí, de ahí te mueves dependiendo de cómo reaccionen los estudiantes. No necesitas empujarlos. Solo ve hacia donde te lleven. Entonces, en algún punto lanza una palabra que los lleve hacia el camino correcto.

P: Sí, eso es.

S: “¿Notan algo en esto?” o algo así. (Dgespetv, 2012)

En ese diálogo podemos inferir que P y S están preocupados por diseñar una tarea que esté a una distancia razonable de aquello que los alumnos saben, pero que al mismo tiempo les exija una alta demanda cognitiva, en el sentido que les lleve a realizar procesos relevantes de la actividad matemática —en este caso, observar una regularidad y formular una conjetura: “Yo creo que los estudiantes van a notar que hay algo aquí” (Dgespetv, 2012)—. En segundo lugar, podemos observar cómo comentan el tipo de gestión que debe hacer el profesor para conseguir que los alumnos tengan éxito ante una tarea poco pautada —“Sí, de ahí te mueves dependiendo de cómo reaccionen los estudiantes. No necesita empujarlos. Solo ve hacia donde te lleven. Entonces, en algún punto lanza una palabra que los lleve hacia el camino correcto” (Dgespetv, 2012)—.

Más adelante, podemos observar cómo P insiste en que ha diseñado la tarea con el objetivo de que los estudiantes hagan conjeturas que les permitan formular las reglas comentadas anteriormente:

P: Pienso que los estudiantes tarde o temprano descubrirán ciertas reglas mientras que tratamos con 1, 2 y 3 como respuestas a la ecuación. Estoy esperando ansiosamente el momento en que descubran las reglas. Voy a resaltar cosas que ellos pueden decir sobre las reglas, de tal forma que el resto de la clase comprenda hasta a dónde vamos. ¿Finalmente, les preguntaré “Cuántas ecuaciones pueden realizar cuando la respuesta es 9?” Llegar al punto donde puedo realizar esta pregunta es crucial. (Dgespetv, 2012)

Posteriormente, en el momento de la reflexión sobre la clase impartida, al ser cuestionado sobre si la clase se había desarrollado como él la había planeado, el profesor comenta lo siguiente:

P: Se desarrolló muy de acuerdo a lo que yo quería que sucediera. Los niños llegaron a las conclusiones exactas que yo quería que descubrieran. Sin embargo, podría tener reunidos o conectados los pensamientos y explicaciones de una mejor manera para ayudar a que todos comprendieran lo que algunos estudiantes estaban diciendo. (Dgespetv, 2012)

En ese párrafo podemos inferir en el discurso de P la importancia dada al indicador los diversos modos de evaluación muestran la apropiación de los conocimientos/competencias pretendidas o implementadas del componente de la idoneidad cognitiva aprendizaje de los alumnos. También se hace evidente el uso implícito del indicador valorar si las interacciones gestionadas en clase resuelven dudas y dificultades de los alumnos del componente interacción docente-discente del criterio de idoneidad interaccional.

Más tarde, el profesor reflexiona por qué algunos alumnos tuvieron dificultades:

P: Es interesante observar que los estudiantes que usualmente son buenos en las matemáticas, tuvieron dificultades en un principio. Me pregunté el porqué más tarde y me dije: Aquellos que son buenos en las matemáticas estaban tratando de dar con el número que va en la columna de las decenas, cuando la diferencia era 3. Aquellos que inesperadamente obtuvieron la respuesta correcta miraron al problema como un todo. Debido a que la diferencia era 3, ellos simplemente llegaron al 100 y 97 inmediatamente. (Dgespetv, 2012)

En esa reflexión se puede inferir el uso implícito del indicador observación sistemática del progreso cognitivo de los alumnos que forma parte del componente evaluación formativa del criterio de idoneidad interaccional.

Un maestro [M1] propone al profesor una forma alternativa de presentar el problema:

M1: Estaba preguntándome por qué no permitiste que los niños intentaran con el número uno. Creo que sería bueno empezar con uno, porque así puedes explicar todo lo que debe ser cubierto en la clase del día de hoy. Aquellos que no son buenos en las matemáticas probablemente tendrán problemas con este. Si el problema fuera por ejemplo 9 – 8 = 1, trabajar con el número uno podría darles a los niños una mejor pista de lo que está sucediendo. (Dgespetv, 2012)

La reflexión realizada por M1 hace hincapié en que los significados pretendidos deben presentar una dificultad manejable, un indicador de la idoneidad cognitiva. En contrapartida, el profesor argumenta:

P: Hoy utilicé el número tres y 27 o 28 estudiantes lo captaron de inmediato. Hubo aproximadamente 10 estudiantes que tardaron un largo tiempo en resolverlo. Si miras el promedio, creo que presentar el problema usando el número tres fue una buena solución. (Dgespetv, 2012)

En esa afirmación, el profesor no tiene en cuenta la diversidad en el ritmo de aprendizaje de sus alumnos, es decir, no contempla el componente adaptación curricular a las diferencias individuales del criterio cognitivo.

Otro maestro [M2] propone al profesor una forma alternativa de desarrollar la tarea:

M2: ¿Tienen esas cartas? ¿Correcto? El problema de restar un número de dos dígitos de uno de tres dígitos que da una diferencia de cinco es, bueno, estaba preguntándome el porqué les está dando inmediatamente las respuestas [comentario de que el profesor les había dado a los estudiantes las respuestas muy prontamente]. Si dejas a los niños resolver los problemas, sería mucho más interesante. Escoge algunos niños al azar, llámalos al pizarrón y pídeles que escriban las respuestas. Creo que eso lo hará más interesante. De esta forma no hay orden en sus respuestas. Si ellos dicen, “hay cinco respuestas” entonces tú dices: “escojamos a 5 estudiantes”. Si les pides que escriban las respuestas, entonces no les presentarás ese orden tan perfecto. Puede haber respuestas duplicadas también. De esa forma ellos podrán ver claramente qué es lo que hace falta. Si haces eso, ¿no hará que los estudiantes trabajen juntos en “poner las ecuaciones en orden correcto”?

En esa reflexión, M2 hace referencia a la posibilidad de usar material manipulativo —cartas— para modificar la forma de interacción en el aula. También hace la sugerencia de que se promueva el componente alta demanda cognitiva del criterio de idoneidad cognitiva; en particular, que se activen procesos cognitivos relevantes —generalización, conexiones intra-matemáticas, cambios de representación, conjeturas…— contemplados en el componente riqueza de procesos de la idoneidad epistémica.

Aunque el profesor en su clase no tuvo en cuenta la diversidad en el ritmo de aprendizaje de sus alumnos —componente del criterio de idoneidad cognitivo—, otro maestro [M3] tiene presente ese aspecto en su reflexión:

M3: Debido a que cada niño puede tomar un camino distinto para descubrir las reglas que el maestro usa, sería mejor enfocarse en cómo cada niño descubre. Al hacer eso, se compartirían dichos descubrimientos con la clase entera para profundizar en el entendimiento de todos. (Dgespetv, 2012)

Por otra parte, el maestro [M4] hace un comentario relacionado con la afectividad entre el profesor y sus estudiantes —componente del criterio de idoneidad emocional—.

M4: El profesor tiene una relación maravillosa con los niños. No creo que nadie pueda construir una relación tal en un día. Él ha tenido que poner un gran esfuerzo día a día con los niños para alcanzar una relación de ese tipo. (Dgespetv, 2012)

Al final del video, P presenta un rediseño de la clase tomando en cuenta las observaciones de mejora sugeridas por los otros profesores que han participado de esta experiencia de EC.

Discusión de los resultados y consideraciones finales

Al analizar las reflexiones de los profesores sobre un proceso de instrucción de una clase —diseño, implementación y reflexión/rediseño— que sigue la metodología del EC, hemos concluido que dicho grupo de profesores utiliza, de manera implícita, algunos de los componentes e indicadores de los CI. En particular, utilizan de manera muy significativa los criterios interaccional y cognitivo, y con menos énfasis los criterios de idoneidad epistémica y emocional. Sin embargo, los criterios de medios y ecológico son poco utilizados en la reflexión del grupo de profesores. El hecho de la poca reflexión alrededor de estos dos últimos criterios se puede deber al propio enfoque EC, o a que estos dos criterios ya estén muy desarrollados en Japón, o bien a una falta de una pauta explícita que contemple todos los elementos que se deben tener en cuenta para reflexionar sobre la realización de un proceso de instrucción matemático y de cómo mejorarlo.

En el análisis realizado se evidencia que en una clase basada en el EC surgen consensos implícitos entre el profesor que desarrolla la clase y los otros profesores participantes sobre criterios de cómo hacer la clase que se valoran positivamente, los cuales se pueden reinterpretar en términos de indicadores y componentes de los CI. En particular, una de las ventajas de trabajar con la dinámica de EC es que algunos de los aspectos que no están presentes en la reflexión del propio profesor, pueden estar presentes en la reflexión de los otros profesores que participan del proceso de instrucción. Dicho de otra manera, la metodología EC se convierte en un tipo de dispositivo de formación que favorece que algunos de los indicadores y componentes de los CI surjan como consensos en la reflexión del grupo de profesores. Este resultado sugiere que para investigar —en la formación del profesor de matemáticas— el desarrollo de la reflexión sobre la práctica en la formación de profesores de matemáticas, un dispositivo adecuado puede ser el diseño e implementación de un dispositivo formativo que combina el uso de los EC y los CI como herramienta metodológica para organizar la reflexión del profesor (Hummes, Font & Breda, 2019; Seckel & Font, 2020).

En relación con los resultados obtenidos en nuestra investigación, un aspecto a explicar es la razón por la cual los CI funcionan implícitamente como regularidades en el discurso de los profesores sin haberles enseñado el uso de esta herramienta para pautar su reflexión. Una explicación plausible (Breda et al., 2018; Hummes et al., 2019; Seckel, Breda, Sánchez & Font, 2019) es que los CI reflejan consensos sobre cómo debe ser una buena enseñanza de las matemáticas ampliamente asumidos en la comunidad de educadores y educadoras. Es plausible pensar que el uso implícito que hace el profesorado de los CI se debe a su formación y experiencia previa, la cual le hace partícipe de dichos consensos. Ahora bien, otra explicación es que el profesor que utiliza estos criterios, al no haber participado en el proceso de generación de los consensos que los soportan, los asuma como regularidades en su discurso simplemente porque, en la formación que ha recibido, se le presentan como algo naturalizado e incuestionable en la formación que ha recibido.

Referencias

Baldin, Y. (2009). O significado da introdução da metodologia japonesa de Lesson Study nos cursos de capacitação de professores de matemática no Brasil. XVIII Encontro Anual da SBPN e Simpósio Brasil-Japão. São Paulo: SBPN.

Breda, A., & Lima, V. (2016). Estudio de caso sobre el análisis didáctico realizado en un trabajo final de un máster para profesores de matemáticas en servicio. Redimat, 5(1), 74-103. doi: 10.4471/redimat.2016.1955.

Breda, A., Font, V., & Lima, V. (2015). A noção de idoneidade didática e seu uso na formação de professores de matemática. Jornal Internacional de Estudos em Educação Matemática, 8(2), 1-41. doi: 10.17921/2176-5634.2015v8n2p%25p

Breda, A., Font, V., & Pino-Fan, L. (2018). Criterios valorativos y normativos en la didáctica de las matemáticas: el caso del constructo idoneidad didáctica. Bolema, 32(60), 255-278. doi: 10.1590/1980-4415v32n60a13.

Breda, A., Font, V., Lima, V., & Pereira, M. (2018). Componentes e indicadores de los criterios de idoneidad didáctica desde la perspectiva del enfoque ontosemiótico. Transformación, 14(2), 162-176.

Breda, A., Pino-Fan, L., & Font, V. (2017). Meta didactic-mathematical knowledge of teachers: criteria for the reflection and assessment on teaching practice. Eurasia Journal of Mathematics, Science and Technology Education, 13(6), 1893-1918. doi: 10.12973/eurasia.2017.01207a.

Brockbank, A., & McGill, I. (2002). Aprendizaje reflexivo en la educación superior. Madrid: Morata.

Burghes, D., & Robinson, D. (2010). Lesson study: enhancing mathematics teaching and learning. Plymouth, UK: CfBT Education Trust, University of Plymouth.

Dewey, J. (1989). Cómo pensamos: Nueva exposición de la relación entre pensamiento y proceso educativo. Barcelona: Paidós.

Dgespetv [DGESPETV]. (12 de junio de 2012). Implementación de un Estudio de Clase [Archivo de video]. Recuperado de https://www.youtube.com/watch?v=e7uPuSaPQSU&t=9s

Fernández, C., & Yoshida, M. (2004). Lesson study: a Japanese approach to improving mathematics teaching and learning. Mahwah: Erlbaum.

Font, V., Planas, N., & Godino, J. (2010). Modelo para el análisis didáctico en educación matemática. Infancia y Aprendizaje, 33(1), 89-105.

Godino, J., Contreras, A., & Font, V. (2006). Análisis de procesos de instrucción basado en el enfoque ontológico-semiótico de la cognición matemática. Recherches en Didactiques des Mathematiques, 26(1), 39-88.

Hart, L., Alston, A., & Murata, A. (2011). Lesson Study Research and Practice in Mathematics Education. Netherlands: Springer.

Huang, R., & Shimizu, Y. (2016). Improving teaching, developing teachers and teacher educators, and linking theory and practice through lesson study in mathematics: an international perspective. ZDM, 48(4), 393-409.

Hummes, V, Font, V., & Breda, A. (2019). Combined Use of the Lesson Study and the Criteria of Didactical Suitability for the Development of the Reflection on the own Practice in the Training of Mathematics Teachers, Acta Scientiae, 21(1), 64-82.

Mallart, A., Font, V., & Malaspina, U. (2016). Reflexión sobre el significado de qué es un buen problema en la formación inicial de maestros. Perfiles Educativos, 38(152), 14-30.

Perrenoud, P. (2004). Diez nuevas competencias para enseñar: Invitación al viaje. Barcelona: Graó.

Pochulu, M., Font, V., & Rodríguez, M. (2016). Desarrollo de la competencia en análisis didáctico de formadores de futuros profesores de matemática a través del diseño de tareas. Revista Latinoamericana de Investigación en Matemática Educativa-RELIME, 19(1), 71-98.

Ponte, J. (1994). O estudo de caso na investigação em educação matemática. Quadrante, 3(1), 3‐18.

Ponte, J., Baptista, M., Velez, I., & Costa, E. (2012). Aprendizagens profissionais dos professores de Matemática através dos estudos de aula. Perspectivas da Educação Matemática, 1(1), 7-24.

Schön, D. (1992). La formación de profesionales reflexivos: hacia un nuevo diseño de la enseñanza y el aprendizaje en las profesiones. Barcelona: Paidós.

Seckel, M., & Font, V. (2020). Competencia reflexiva en formadores del profesorado en matemáticas. Magis, 12(25), 127-144.

Seckel, M. (2016). Competencia en análisis didáctico en la formación inicial de profesores de educación general básica con mención en matemática (Tesis doctoral inédita. Universitat de Barcelona, Barcelona, España).

Seckel, M., Breda, A., Font, V., & Sánchez, A. (2019). Criterios asumidos por profesores cuando argumentan sobre la creatividad matemática. Educação e Pesquisa, 45, e211926.

Seckel. M., & Font, V. (2015). Competencia de reflexión en la formación inicial de profesores de matemática en Chile. Praxis Educacional, 11(19), 55-75.

Yin, R. (2001). Estudo de caso: planejamento e métodos. Porto Alegre: Bookman.

Yoshida, M. (2012). Mathematics lesson study in the United States: current status and ideas for conducting high quality and effective lesson study. International Journal for Lesson and Learning Studies, 1(2), 140-152.

---