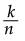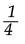Intente encontrar un proceso que, a partir de la derivada que acaba de hallar, regrese a la función original o a otra muy parecida.Transcripción del discurso de clase
La profesora comienza anunciando que van a trabajar el concepto de antiderivada.
1. P: Dada una función f(x) entonces se dice que es la antiderivada de F(x), si . —Mientras escribe la definición de antiderivada en el tablero, también la comunica verbalmente—.
2. P: Para entender la noción de antiderivada, recordemos la derivada de funciones de la forma f(x) = kxn.
—En el tablero:
Si f(x) = xn entonces f ’(x) = nxn-1
3. P: En ese orden de ideas ¿recuerdan la derivada de f(x) = x2 ?
—En el tablero:
Ejemplo: Si f(x) = x2 ; entonces f ‘(x) = ?
4. E1: La derivada es dos equis [f ‘(x) = 2x]
5. P: Ahora hallen la derivada de las siguientes funciones.
—En el tablero:
f(x) = x3
f(x) = – 5x5
f(x) = 6x-2
f(x) = – 8x-1/2
f(x) = x1/2
6. E2: Profe, cuando la función está multiplicada por una constante, ¿se debe hacer regla del producto?
7. E1: Por ser constante, no es necesario hacer el [regla del] producto. Se puede dejar quieta la constante y derivar la función. ¿Cierto, profe?
8. P: —A E1— Estás en lo cierto.
9. E3: Profe, yo lo hice por regla del producto y me da el mismo resultado que a E1.
10. P: Los dos procedimientos son válidos. Lo ideal sería que utilicen la propiedad, ya que simplifica los cálculos.
—En el tablero:
Si f(x) = kxn, entonces f ’(x) = k(nxn-1).
—La profesora pasa observando la solución de los ejercicios de algunos estudiantes—.
11. P: Ahora vamos a trabajar con las mismas funciones, para hallar la antiderivada. Retomemos la definición —señala la definición que escribió al inicio de la clase—. Ahora ya no se deriva la función, se busca una función que al derivarla se pueda recuperar la función inicial f(x)
—En el tablero:
Ejemplo: Si f(x) = x3 ; entonces F(x) = ?
12. P: ¿Cuál es la función que al derivarla da equis al cubo?
13. E2: Profe, yo sé. ¿Puedo pasar al tablero?
—La profesora le entrega el marcador a E2, mientras hace una señal de afirmación—.
14. E2: —En el tablero:
F(x) = x4
F ‘(x) = 4x3
—E2 queda pensativa y resalta el número cuatro—.
15. E4: Y ahora, ¿qué hacemos con ese cuatro?
16. E2: Profe, ¿qué hacemos para que se vaya [eliminar] el cuatro?
17. P: —En el tablero la profesora aclara lo que E2 lleva escrito—.
F(x) = x4 F ‘(x) = 4x3 f(x) = 1x3
Si F(x) = x4 entonces F ‘(x) = f(x) = x3
18. P: —Señala en el tablero—. Podemos ver que el coeficiente de equis al cubo es uno. ¿Qué operación hacemos para que el cuatro se simplifique? Es decir, que no aparezca; se elimine.
19. E5: Profe, podemos dividir en cuatro y nos da equis al cubo.
20. P: —A E5— ¿En dónde dividimos en cuatro?
— Señala al tablero en:
F‘(x) = 4x3 o F(x) = x4 .
21. E5: En F‘(x).
22. E3: —A E5—. Yo creo que es en F (x).
23. P: ¿Qué es lo que estamos hallando? ¿La antiderivada F(x) o la derivada de la antiderivada F‘(x)?
24. E6: Profe, la antiderivada.
25. P: Bueno, en ese orden de ideas, ¿cuál sería la antiderivada de equis al cubo?
26. E4: Queda así —pasa y escribe en el tablero—:
F (x) =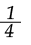 x4
x4
27. P: Ahora verifiquemos que la derivada de F‘(x) = f(x)
—En el tablero:
F (x) = 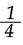 (4x3)
(4x3)
F (x) = 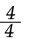 x3 = x3 = f(x)
x3 = x3 = f(x)
28. P: Ahora en la siguiente tabla relacione cada función con su derivada y su antiderivada.
—En el tablero:
Función f(x) | Derivada f ’(x) | Antiderivada F(x) |
x3 | 3x2 | 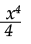
|
– 5x5 | –25x4 | – 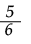 x6 x6 |
– 6x-2 | –12x-3 | 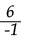 x-1 x-1 |
– 8x-1/2 | 4x-3/2 | – 16x1/2 |
x1/2 | 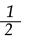 x-1/2 x-1/2
| 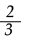 x3/2 x3/2
|
. . . | . . . | . . . |
kxn | kxn-1 | 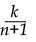 xn+1 xn+1
|
—Pasados unos minutos, la profesora comienza a pasar a los estudiantes al tablero para discutir conjuntamente las respuestas encontradas—.
29. P: Ahora van hacer grupos de cinco estudiantes y van a socializar cómo sería una posible generalización del cálculo de la antiderivada para funciones de la forma f(x) = kxn.
Discusión del grupo que llegó a la generalización.
Grupo 5
30. E7: No entiendo. ¿Qué debemos hacer?
31. E3: Según entiendo, debemos encontrar una fórmula que sirva para encontrar la antiderivada de cualquier función de esa forma: kxn —señala al tablero—.
32. E7: Nos toca hacer lo mismo que estas funciones —señala las funciones trabajadas en la tabla—.
33. E20: — A E3— Yo creo que la fórmula es 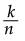 xn+1 .
xn+1 .
34. E3: Profe, ya tenemos la fórmula. Es 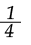 xn+1.
xn+1.
35. P: Pueden verificar si les quedó bien tomando una de las funciones trabajadas en la tabla. Por ejemplo, prueben con esta función f(x) = x3 —señala en el cuaderno de un estudiante—.
36. E20: ¿Entonces el valor de en este caso sería 1, y n sería 3?
37. E3: ¿Por qué k es 1?
38. E20: Porque 1 es el coeficiente de x4.
39. E7: Es decir 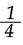 x3+1 ¡hum! —queda pensativa—.
x3+1 ¡hum! —queda pensativa—.
40. E20: Entonces quedaría F(x) = 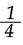 x4—muestra en el cuaderno—.
x4—muestra en el cuaderno—.
41. P: Según los ejemplos trabajados en clase, el denominador de la fracción queda igual al exponente de la expresión —señala en el cuaderno de un estudiante—.
42. E20: Profe, estaba pensando que me quedó diferente. ¿Entonces qué hacemos para que el 3 quede como un 4?
43. E3: Pues, en el denominador le podemos sumar uno igual que al exponente, como aquí —señala en su cuaderno—. Entonces debemos cambiar la fórmula.
44. P: ¿Entonces cómo quedaría?
45. E7: —A E3— Pues entonces la fórmula que propusiste está bien, solo que en el denominador le debes sumar uno, como dijiste. Así —le muestra en el cuaderno—
F(x) = 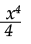 x3+1
x3+1
46. P: Pero no han contestado cómo queda la generalización para cualquier fórmula.
47. E3: Quedaría así 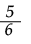 xn+1.
xn+1.
48. P: Muy bien. Aún no digan su conjetura. En un momento hacemos plenaria.
—La profesora pregunta grupo por grupo si ya pueden empezar a socializar las respuestas—.
49. P: Listo, como ya trabajaron en grupo, vamos a socializar las generalizaciones a las cuales llegaron. Por favor, pase un representante de cada grupo y cuéntenos a qué generalización llegaron.
50. G1: En nuestro grupo cada uno trabajó solo y al final seleccionamos la correcta.
—En el tablero:
F(x) =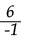 xn+1.
xn+1.
51. G2: Solo trabajamos dos porque los demás se limitaron a escuchar y a escribir.
—En el tablero:
F(x) = k(n+1) xn+1.
52. G3: Nosotros tomamos la función f(x) = x3 y cambiamos el exponente por
—En el tablero:
F(x) =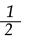 .
.
53. G4: Nosotros llegamos a la misma respuesta que ellos —señala a G1—.
—En el tablero:
F(x) =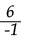 xn + 1
xn + 1
54. P: Pero cuéntenos cómo llegaron a esa respuesta.
55. G4: Yo les dije que esa podría ser y ellos estuvieron de acuerdo.
56. G5: Inicialmente un compañero propuso una fórmula. Nosotros la empezamos a probar con los ejemplos y nos dimos cuenta de que estaba mal. La íbamos corrigiendo hasta que llegamos a la fórmula que creemos es la correcta.
—En el tablero:
F(x) = k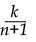
57. P: Retomemos nuevamente la función f(x)= – 5x5 y comprobemos con cada una de las generalizaciones si llegan a su correspondiente antiderivada. Cada uno haga el ejercicio en el cuaderno.
—Aproximadamente pasados 10 minutos, los estudiantes empezaron a discutir—.
58. E10: Profe, con la única que me da es con la última fórmula —señala en el tablero la fórmula que escribió el G5—.
59. E20: Sí, profe, con la única que da la respuesta correcta es con nuestra fórmula.
—En ese momento todos empezaron a opinar que la generalización correcta fue a la que llego el G5—.
60. P: Muy bien chicos. Como pueden ver, es importante que ustedes formen parte en la construcción de conceptos, en este caso el de la antiderivada. Por tiempo no alcanzamos a analizar la antiderivada de las funciones exponencial, logarítmica y trigonométrica. Pueden ir revisando las siguientes funciones como tarea y las socializamos la siguiente clase.
—En el tablero:
f(x)=ex, f(x)=lnx, f(x)=senx, f(x)=cosx, f(x)=tanx, f(x)=cotx, f(x)=secx, f(x)=cscx,
—Se vio una satisfacción personal en los estudiantes que lograron llegar a la generalización, y también en los estudiantes que se aproximaron a dicha solución. En general se notó un ambiente agradable y motivante en los estudiantes en el transcurso de la clase—.
Análisis didáctico de la clase de matemáticas.
Para facilitar el análisis de la clase, se ha dividido en cuatro momentos de clase, los cuales se denotan como S1: [1-10], S2: [11-28], S3: [29-48] y S4: [49-60]. Cada momento se determinó teniendo en cuenta la realización de una tarea.
Identificación de objetos matemáticos.
En la figura 1 se muestra la identificación de los objetos primarios propuestos en el marco teórico y metodológico del EOS, realizada a partir de la transcripción.
Facetas duales.
En la figura 1, se clasificaron los objetos primarios de la clase por cada uno de los momentos. Esto permitió identificar la intervención de las facetas duales —objetos secundarios—, las cuales se describen a continuación:
Personal-institucional.
Este tipo de objetos se presentó en el momento en que la docente comenzó a construir el concepto de antiderivada. Hizo que el estudiante partiera de los conceptos ya adquiridos sobre el concepto de derivada. En la realización de ejercicios de profundización y en la construcción de la definición formal, se evidenció que tanto los estudiantes como la docente argumentaron de forma verbal sus ideas y conjeturas. La docente pasó a ser facilitadora del aprendizaje de dicho concepto y los estudiantes a ser partícipes en la construcción del mismo. Sin embargo, en el transcurso de la clase se desarrollaron ejercicios netamente de naturaleza algorítmica. En este sentido se esperaría que estos objetos estuvieran presentes en cada momento de la clase, ya que la cognición personal es el resultado del pensamiento y la acción del sujeto individual ante una cierta clase de problemas, mientras la cognición institucional es el resultado del diálogo, el convenio y la regulación en un grupo de individuos que forman una comunidad de prácticas (Godino et al. 2008, p. 8).
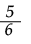
Figura 1. Identificación de objetos matemáticos de la clase. Fuente: adaptado de Londoño y López (2016).
Unitario-sistémico.
Estos objetos se identificaron cuando la docente, antes de definir antiderivada, partió del concepto de derivada —conceptos previos— y desarrolló algunos ejercicios teniendo en cuenta propiedades y operaciones algebraicas que ya debían manejar —conceptos previos—. De igual forma, involucró a los estudiantes al hacer que justificaran las respuestas obtenidas en cada ejercicio. Luego, docente y estudiantes participaron en el diligenciamiento de una tabla, lo cual los llevó a construir el concepto de antiderivada de funciones potencia. Estos objetos matemáticos —derivada— participaron como entidades unitarias —que se suponen son conocidas previamente—, mientras que otras —antiderivada— intervinieron como sistemas que se deben descomponer para su estudio (Godino et al. 2008).
Cabe aclarar que, en la construcción del concepto de antiderivada de otro tipo de funciones, la docente pretendía involucrar de forma similar a los estudiantes, pero esto no fue posible por tiempo.
Expresión-contenido.
El objeto expresión se presentó continuamente en la construcción del concepto de antiderivada a través del desarrollo de ejercicios y de su argumentación con la participación de la docente y de los estudiantes. El objeto contenido se presentó cuando los estudiantes, a partir del concepto recordado de derivada construyeron el concepto de antiderivada. De esta forma, los distintos objetos no se deben concebir como entidades aisladas, sino puestos en relación unos con otros. La relación se establece por medio de funciones semióticas, entendidas como una relación entre un antecedente —expresión, significante— y un consecuente —contenido, significado— establecida por un sujeto —persona o institución— de acuerdo con un cierto criterio o código de correspondencia (Godino et al. 2008, p. 8).
Extensivo-intensivo.
Estos objetos se presentaron implícitamente durante el desarrollo de la clase. Permitieron centrar la atención en la dialéctica entre lo particular y lo general, puesto que se construyó el concepto de antiderivada a partir de la definición de las derivadas de los diferentes tipos de funciones potencia, lo cual permitió, a partir de las conjeturas, llegar a la definición formal de antiderivada. En consecuencia, esta dualidad permite centrar la atención en la dialéctica entre lo particular y lo general, que sin duda es una cuestión clave en la construcción y aplicación del conocimiento matemático (Godino et al. 2008, p. 8).
Identificación de procesos matemáticos.
A continuación, se muestra la identificación de los procesos cognitivos/epistémicos en cada uno de los momentos, realizada a partir de la transcripción.
S1 [1-10]: Determinación de las derivadas de algunas potencias.
Docente.
Proceso de significación: define antiderivada [1].
Proceso de generalización, representación, reificación e institucionalización: recuerda derivada de las funciones de la forma f (x)= xn [2].
Proceso de representación y materialización: propone ejercicios en el tablero [5].
Proceso de idealización, materialización y significación: explica la derivada de una función por una constante, lo hace de forma verbal y simbólica [10].
E1.
Proceso de idealización y reificación: expresa verbalmente que la derivada es dos equis [4]; expresa que no es necesario aplicar la regla del producto para derivar la función [7].
E2.
Proceso de idealización y reificación: pregunta verbalmente a la profesora “cuando la función está multiplicada por una constante, ¿es necesario hacer regla del producto? [6].
E3.
Proceso de personalización, reificación e idealización: expresa verbalmente que derivó la función por regla del producto y le da el mismo resultado obtenido por un compañero [9].
S2 [11-28]: Determinación de la antiderivada de funciones de la forma f (x)= kxn.
Docente.
Proceso de institucionalización, representación y materialización: escribe en el tablero la primera función f (x)= x3. para antiderivar [11]; verifica que la antiderivada es f(x)=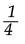 x4 [27]; propone a los estudiantes relacionar en una tabla la derivada y antiderivada de las funciones trabajadas [28].
x4 [27]; propone a los estudiantes relacionar en una tabla la derivada y antiderivada de las funciones trabajadas [28].
Proceso de institucionalización, idealización y descomposición: aclara lo que E2 lleva escrito [17]; explica y cuestiona sobre el coeficiente de la función f (x)= x3, [18].
E2.
Proceso de personalización y reificación: expresa la antiderivada de f (x)= x3 y verifica derivando F(x)= x4 [17].
E3.
Procesos de idealización: expresa verbalmente que cree que cuatro se debe dividir a F(x)[22].
E4.
Proceso de representación y materialización: pasa y escribe en el tablero la antiderivada de equis al cubo F’(x) [26].
E5.
Proceso de idealización: expresa verbalmente que se puede dividir en cuatro para que dé equis al cubo [19]; responde a la profesora que se divide en cuatro [21].
S3 [29-48]: Determinación de la forma general de las antiderivadas de funciones del tipo kxn, n ≠ –1 .
Docente.
Proceso de institucionalización e idealización: les indica a los estudiantes del G5 que pueden verificar la fórmula y sugiere que trabajen con la función f(x)= x3 [35]; indica a los estudiantes que al verificar la fórmula de la antiderivada, el exponente de la función debe ser igual que el denominador de la fracción [41]; cuestiona y guía a los estudiantes del grupo [44, 46 y 48].
E3.
Proceso de idealización: explica a su compañero que deben encontrar una fórmula que sirva para antiderivar cualquier función de la forma kxn [31]; indica a la profesora que ya encontraron la fórmula [34]; pregunta a su compañero “¿por qué k debe ser 1?” [37].
Proceso de personalización, materialización y representación: deduce que en el denominador de la fracción le pueden sumar uno, igual que en el exponente, y por esto deben cambiar la fórmula [43]; muestra a la profesora que la fórmula de antiderivada de función potencia es F(x) =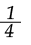 xn+1. [47].
xn+1. [47].
E7.
Proceso de idealización: expresa que no entiende lo que tienen que hacer [30]; señala al tablero y expresa que entiende que hay que hacer lo mismo que se hizo en el tablero [32]; indica a E3 que la fórmula que propuso está bien y lo único que hay que hacer es agregarle más uno en el denominador [32].
Proceso de materialización: escribe en el cuaderno 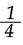 x3+1 [39]; expresa y muestra en su cuaderno F(x)=
x3+1 [39]; expresa y muestra en su cuaderno F(x)= 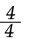 x3+1 [45].
x3+1 [45].
E20.
Proceso de idealización: pregunta a la profesora “¿entonces el valor de k en este caso sería 1 y n sería 3?” [36]; expresa que uno es el coeficiente de x3 [38]; dice a la profesora que le quedó diferente y le pregunta qué deben hacer para que, en lugar de tres, dé cuatro [42].
Proceso de materialización: escribe en el cuaderno F(x)= 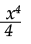 x4 [40].
x4 [40].
S4 [49-60]: Socialización y verificación de la forma general de las antiderivadas de funciones del tipo kxn, n ≠ –1. Derivadas y antiderivadas de otro tipo de funciones.
Docente.
Proceso de idealización: indica a los estudiantes que se van a socializar las respuestas y para esto debe pasar un representante de cada grupo [49]; indica a G4 que diga cómo llegaron a la fórmula que escribió en el tablero [54]; indica a los estudiantes retomar la función f(x)= – 5x5 para verificar cada una de las fórmulas socializadas por los grupos y así identificar con cuál de todas hallan la antiderivada F(x)= 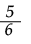 x6 [57].
x6 [57].
Proceso de materialización, institucionalización e idealización: escribe en el tablero las funciones f(x)=ex, f(x)=lnx, f(x)=senx, f(x)=cosx, f(x)=tanx, f(x)=cotx, f(x)=secx, f(x)=cscx, y les indica que queda como tarea analizar cómo serían las antiderivadas de estas funciones [60].
G1.
Proceso de idealización y materialización: expresa verbalmente que cada integrante del grupo trabajó solo y al final seleccionaron la fórmula que creyeron correcta; escribe en el tablero F(x)= 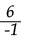 xn+1 [50].
xn+1 [50].
G2.
Proceso de idealización y materialización: expresa verbalmente que solo trabajaron dos y que los demás se limitaron a escuchar y a escribir en el tablero F(x)= k(n+1) xn+1 [51].
G3.
Proceso de idealización y materialización: expresa verbalmente que tomaron como ejemplo la función f(x)=x3 y cambiaron el exponente por ; escribe en el tablero F(x)=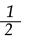 [52].
[52].
G4.
Proceso de idealización y materialización: expresa verbalmente que llegaron a la misma respuesta que el grupo G1; escribe en el tablero F(x) =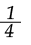 xn + 1 ; dice que encontró la fórmula que creía era la correcta y los demás estuvieron de acuerdo [53].
xn + 1 ; dice que encontró la fórmula que creía era la correcta y los demás estuvieron de acuerdo [53].
G5.
Proceso de idealización y materialización: expresa verbalmente que inicialmente un compañero propuso una fórmula y ellos la empezaron a comprobar con los ejemplos y se dieron cuenta de que estaba mal, y la iban corrigiendo hasta que llegaron a la fórmula que creyeron correcta y al escribir en el tablero F(x) = k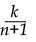 [56].
[56].
E10.
Proceso de idealización: expresa verbalmente que la única fórmula que sirve para hallar la antiderivada es la expuesta por el G5 [58].
Teniendo en cuenta lo anterior, se puede ver que los procesos cognitivo-epistémicos por parte de la profesora en su mayoría fueron de institucionalización, representación, materialización, idealización y reificación, ya que por lo general la docente, en el momento de aclarar dudas, explicó los procedimientos de manera minuciosa y detallada. Expresó verbal y simbólicamente las propiedades y operaciones algebraicas necesarias para la solución de los mismos. Además, implícitamente, en el transcurso de la clase se presentaron procesos de significación, generalización y particularización, dado que el objetivo principal del desarrollo de las prácticas operativas y discursivas de la docente fue involucrar al estudiante en la definición formal de antiderivada.
Los procesos más comunes manifestados por los estudiantes fueron los de representación, materialización e idealización, puesto que la clase se desarrolló alrededor de la participación de los estudiantes, con la solución de algunos ejercicios en el cuaderno. Muy pocas veces se presentaron procesos de personalización y reificación, ya que la forma en que la docente dio su clase no permitió identificar si estudiantes entendieron o no los significados pretendidos.
Conflictos semióticos.
El análisis de los objetos primarios (figura 1) y los procesos matemáticos ayudaron a identificar algunos de los conflictos semióticos presentados en el desarrollo de la clase, tales como:
- En el momento que E2 realizó los procesos de idealización y reificación, se identificó un conflicto semiótico de tipo cognitivo, ya que el estudiante no entendió qué regla de derivación tenía que aplicar —conceptos previos—. De igual forma, se presentó un conflicto de tipo interaccional en su relación con la docente y sus compañeros al expresar términos de forma inadecuada [6].
- Cuando E3 realizó el proceso de idealización, se identificó que se generó un conflicto cognitivo, ya que el estudiante no entendía por qué el coeficiente de k era 1 [37].
- En E7, al realizar el proceso de idealización, se identificó que se generó un conflicto cognitivo, al expresar no entender lo que se debía hacer [30].
- Cuando E20 realizó el proceso de idealización, se identificó que se generó un conflicto cognitivo, en el momento que expresó no saber qué hacer para que le diera cuatro en el denominador de la expresión en lugar de tres [42].
Se puede concluir que los conflictos generados en los cuatro estudiantes son de tipo cognitivo. Esto se debe a vacíos que traían en el dominio de conceptos previos. Por tal razón, no lograron deducir qué debían hacer en el momento que la docente les propuso encontrar la antiderivada de cualquier función.
Conclusiones
Como profesores de matemáticas, consideramos que durante el desarrollo de la clase las prácticas son implementadas únicamente por el docente. A partir del estudio de los objetos y procesos matemáticos, se logró intuir que el estudiante también realiza prácticas matemáticas en el desarrollo de los procesos de enseñanza y aprendizaje, ya que a partir de estas se pudieron identificar los conflictos semióticos que se generaron y las normas que son propias de cada proceso.
A partir de la determinación de objetos y procesos matemáticos de la clase, se identificó que la forma en la que el docente comunica los significados institucionales en los procesos de enseñanza y aprendizaje incide significativamente en la apropiación y comprensión de los conceptos por parte de los estudiantes. Esto se pudo percibir cuando la docente propuso a los estudiantes hacer grupos de trabajo con el objetivo de encontrar una posible generalización del cálculo de la antiderivada para funciones potencia.
Al identificar las prácticas y dividir las clases de la docente en momentos, se observa que ella trata de involucrar los conceptos previos que el estudiante tiene sobre derivada para introducir la definición de antiderivada, con el fin de involucrar al estudiante en la construcción de dicha definición. En este sentido, se evidencia la presencia de la dualidad unitario-sistémico, ya que la docente, antes de definir antiderivada, partió del concepto de derivada. Estos objetos matemáticos —derivada— participaron como entidades unitarias —que se suponen son conocidas previamente—, mientras que otros —antiderivada— intervinieron como sistemas que se deben descomponer para su estudio (Godino et al. 2008).
Es necesario que la docente implemente en sus prácticas situaciones problema que le permitan al estudiante tener una visión amplia sobre las aplicaciones de los conceptos e implemente diferentes estrategias para involucrar al estudiante de forma activa en el desarrollo de los procesos de enseñanza y aprendizaje, con el fin de identificar los significados alcanzados, los cuales permiten valorar si el estudiante está comprendiendo los contenidos enseñados.
Referencias
D’Amore , B., Font, V., & Godino, J. (2007). La dimensión metadidáctica en los procesos de enseñanza y aprendizaje de las matemáticas. Paradigma, 28(2), 49-77.
Font, V. (2007). Una aproximación ontosemiótica a la didáctica de la derivada. En A. Maz, B. Gómez & M. Torralbo (Eds.) Noveno Simposio de la Sociedad Española de Educación Matemática SEIEM (pp. 111-128). Córdoba: Sociedad Española de Investigación en Educación Matemática, SEIEM.
Font, V., & Godino, J. (2006). La noción de configuración epistémica como herramienta de análisis. Educaçao Matemática Pesquisa, 8(1), 67-98.
Godino, J. (2002). Un enfoque ontológico y semiótico de la cognición matemática. Recherches en Didactiques des Mathematiques, 22(2-3), 237-284.
Godino, J. (2013). Indicadores de la idoneidad didáctica de procesos de enseñanza y aprendizaje de las matemáticas. Cuadernos de Investigación y Formación en Educación Matemática, (11), 111-132.
Godino, J., & Batanero, C. (1994). Significado institucional y personal de los objetos matemáticos. Recherches en Didactique des Mathématiques, 14(3), 325-355.
Godino, J., Batanero, C., & Font, V. (2007). The Onto-Semiotic Approach to Research in Mathematics Education. ZDM. The International Journal on Mathematics Education, 39(1-2), 127-135.
Godino, J., Batanero, C., & Font, V. (2008). Un enfoque ontosemiótico del conocimiento y la instrucción matemática. Acta Scientiae. Revista de Ensino de Ciências e Matemática, 10, 7-37.
Godino, J., Batanero, C., & Roa, R. (2005). An onto-semiotic analysis of combinatorial problems and the solving processes by university students. Educational Studies in Mathematics, 60 (1), 3-36.
Godino, J., Bencomo, D., Font, V., & Wilhelmi, M. (2006). Análisis y valoración de la idoneidad didáctica de procesos de estudio de las matemáticas. Paradigma, 27(2), 221-252.
Godino, J., Contreras, A., & Font, V. (2006). Análisis de procesos de instrucción basado en el enfoque ontológico-semiótico de la cognición matemática. Recherches en Didactiques des Mathematiques, 26(1), 39-88.
Godino, J., & Font, V. (2007). Algunos desarrollos de la teoría de los significados sistémicos. Recuperado de https://www.ugr.es/~jgodino/funciones-semioticas/anexo1_significados%20sistemicos.pdf
Godino, J, Font, V., & Wilhelmi, M. R. (2006). Análisis ontosemiótico de una lección sobre la suma y la resta, Revista Latinoamericana de Investigación en Matemática Educativa, Vol. Especial, 131-155.
Godino, J., Font, V., Wilhelmi, M., & Castro de, C. (2009). Aproximación a la dimensión normativa en Didáctica de la Matemática desde un enfoque ontosemiótico. Enseñanza de las Ciencias, 27(1), 59-76.
Londoño, J., & López, J. (2016). Análisis ontosemiótico de una propuesta de enseñanza del objeto matemático función en los reales: Un estudio para estudiantes que aspiran a programas de ingeniería. Revista Tecné, Episteme y Didaxis: TED, (9). 1398-1406
Martínez, P. (2006). El método de estudio de caso: Estrategia metodológica de la investigación científica. Pensamiento & Gestión, (20), 165-193.


 , Nury Yolanda Suárez Avila
, Nury Yolanda Suárez Avila
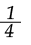
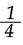 (4x
(4x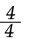 x
x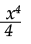
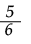
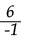
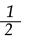 x
x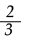 x
x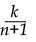 x
x