Research and study paths in physics and mathematics in secondary schools

Abstract

This article reports the results of a research project aimed at developing, analyzing, and evaluating genuinely co-disciplinary research and study paths [RSP] in secondary schools. The implementation and analysis of an RSP in physics and mathematics is presented. The instrument was implemented in five regular mathematics classes in different schools in the district of Tandil, Argentina. A total of 116 students between 16 and 18 years of age took part. The anthropological theory of the didactic, the RSP theoretical concepts, and the Herbartian schema are used as theoretical referents. This article describes and analyzes in detail the generation process of the didactic environment—mesogenesis—in each implementation. The obtained results allow the identification of difficulties in organizing and developing a study environment in the classroom as proposed strictu sensu in an RSP. The analysis of mesogenesis allows deducing some conclusions about the ecology of this type of teaching in regular secondary school courses.

Keywords: education, science teaching, secondary school, research and study path [RSP], didactic environment

Percurso de estudo e de pesquisa em física e matemática nas escolas secundárias

Resumo

Este artigo apresenta os resultados de uma pesquisa que visa desenvolver, analisar e avaliar percursos de estudo e de pesquisa [PEP] genuinamente co-disciplinares nas escolas secundárias. Apresenta-se a implementação e a análise de um PEP em física e matemática. O instrumento foi implementado em cinco aulas regulares de matemática em diferentes escolas do distrito de Tandil, Argentina. Participaram 116 estudantes entre 16 e 18 anos de idade. A teoria antropológica do didático, os conceitos teóricos do PEP e o esquema herbartiano são usados como referentes teóricos. Este artigo descreve e analisa detalhadamente o processo de geração do meio didático — mesogênese — em cada implementação. Os resultados obtidos permitem a identificação de dificuldades na organização e desenvolvimento de um meio de estudo em sala de aula como proposto strictu sensu num PEP. A análise da mesogênese permite deduzir algumas conclusões sobre a ecologia deste tipo de ensino nos cursos regulares de ensino médio.

Palavras-chave: educação, ensino de ciências, escola secundária, percurso de estudo e de pesquisa [PEP], meio didático

En la enseñanza escolar actual predominan prácticas de enseñanza contrarias al cuestionamiento del saber, que ignoran el papel central de las preguntas en el proceso de generación de conocimiento (Chevallard, 2013; Otero et al., 2013). En la escuela, habitualmente se estudian saberes que son o que han surgido como respuestas a preguntas que se desconocen o que están implícitas, y por lo tanto la razón de ser de esos saberes permanece velada. Este hecho produce fenómenos didácticos que Chevallard (2007, 2013) ha definido como monumentalización del saber y pérdida de sentido, a partir de los cuales el saber propuesto para enseñar no es cuestionado y se estudia como un fin en sí mismo.

El monumentalismo es una metáfora construida por la teoría antropológica de lo didáctico [TAD] para describir el fenómeno didáctico que consiste en tratar al saber matemático como un monumento. El Museo del Louvre, el Panteón de París, la pirámide de Chichén Itzá, la catedral de Milán y la ciudad inca de Machu Pichu son monumentos a los cuales se invita a admirar, visitar, preservar, conservar, inmortalizar e incluso amar. En el paradigma monumentalista se concibe y se trata al saber de ese modo. Una de sus características es que los profesores a lo sumo invitan a los estudiantes a visitar el saber, sin alterarlo, transformarlo o deconstruirlo (Chevallard, 2007, 2013). En la epistemología monumentalista el saber se considera inmutable en el tiempo —es suficiente mostrarlo—, de allí el tratamiento ostensivo del que es objeto.

La TAD (Chevallard, 2013; Otero et al., 2013) propone sustituir al paradigma monumental por otro aún emergente, llamado paradigma del cuestionamiento del mundo [PCM], a la vez que desarrolla dispositivos didácticos para enseñar bajo este paradigma, denominados recorridos de estudio e investigación [REI] (Chevallard, 2007, 2009, 2013; Otero et al., 2013). En un REI, los saberes surgen del estudio y del desarrollo de una pregunta cuya respuesta no es conocida de antemano. No pueden ser obtenidos mediante una simple búsqueda de información, sino que es necesario elaborarlos estudiando saberes de diversas disciplinas (Parra & Otero, 2017). La pregunta que da origen a un REI es llamada generatriz, porque posibilita la formulación de una gran cantidad y variedad de otras preguntas derivadas a partir de ella, que es preciso responder para elaborar una posible respuesta final.

Para llevar a cabo un REI, se debe construir un medio de estudio adecuado. La TAD utiliza una metáfora ecológica a partir de la cual considera al medio didáctico como un ambiente apropiado para elaborar las respuestas, en términos de los conocimientos necesarios y los instrumentos requeridos.

A diferencia de lo que sucede en una enseñanza “monumental”, donde el profesor es el único responsable de la construcción del medio didáctico, en un REI el medio es abierto. Existen múltiples fuentes de información en igualdad de condiciones y el estudiante también es responsable de su construcción. Este trabajo se enfoca en presentar y analizar los principales resultados acerca del proceso de construcción del medio didáctico —mesogénesis—, durante cinco implementaciones de un REI que involucra la física y las matemáticas. Se describen las preguntas formuladas, los saberes estudiados, los recursos utilizados y las respuestas elaboradas. Las preguntas de investigación son: ¿cuáles son los saberes de física y de matemáticas principalmente involucrados en el REI y cuáles pueden tratarse en la escuela secundaria? y ¿qué características tiene la construcción del medio didáctico en los recorridos implementados?

Por otro lado, el análisis nos conduce a proponer una posible herramienta para organizar el medio didáctico, conocer el estado del recorrido y posibilitar el acceso a los recursos. Finalmente, trazamos algunas conclusiones sobre la ecología de una enseñanza no monumental en cursos usuales de la escuela secundaria.

Antecedentes

La investigación relativa a cómo enseñar mediante REI tiene poco más de diez años de desarrollo. Se han llevado a cabo REI monodisciplinares —matemáticos— y codisciplinares —involucran más de una disciplina— en la escuela secundaria y en la universidad. La implementación de REI codisciplinares ha sido mayoritariamente en el nivel universitario. Por ejemplo, Serrano et al., (2010), Fonseca (2011) y Salgado et al. (2017) realizaron recorridos que involucran matemáticas y economía; el trabajo de Barquero (2009) presenta un REI relativo a las matemáticas y a la biología; por su parte, Costa et al. (2014) proponen un REI en matemáticas y física; Oliveira-Lucas (2015), uno referido a las matemáticas y a la medicina nuclear; y Barquero et al. (2016), uno en matemáticas y ciencias empresariales. En la escuela secundaria hay menos estudios realizados: los trabajos de Ruiz et al. (2007), Donvito et al. (2014), Parra et al. (2013) y Parra y Otero (2017) son sobre matemáticas y economía; el de Sala et al. (2018) se refiere a las matemáticas y a la historia; el de Kozuoka y Miyakawa (2018), a la biología y las matemáticas; y, por último, está nuestra investigación, en la que proponemos un REI relativo a las matemáticas y la física (Gazzola, 2018). Los resultados de estas investigaciones dan cuenta de las restricciones y de las condiciones que afectan el desarrollo de los REI en los sistemas de enseñanza actuales (Baquero, 2009; Costa et al., 2014). Además, se señalan problemas relativos a los cambios que se requieren en todas las funciones didácticas, especialmente en el nivel mesogenético (Oliveira-Lucas, 2015; Parra et al., 2013; Serrano et al., 2010).

En los REI codisciplinares mencionados, las matemáticas juegan un papel preponderante y las demás disciplinas tienen un lugar reducido a enmarcar la cuestión. El REI propuesto en nuestra investigación involucra las matemáticas y la física de igual forma (Gazzola, 2018; Gazzola et al. 2020; Otero et al. , 2016). No hay una disciplina que prevalezca o que resulte una excusa para estudiar la otra. Ambas tienen un papel central y para elaborar una respuesta es preciso estudiar ambas conjuntamente. La pregunta de este REI carece de una respuesta previamente fundada y, por lo tanto, el equipo de investigación —investigadores formados en matemáticas y física—, al ignorar la respuesta, tuvo que elaborar una propia. La codisciplinariedad en un REI es importante para romper con la fragmentación disciplinar de las instituciones escolares y para permitir que los saberes surjan como instrumentos necesarios para dar respuestas a ciertas preguntas planteadas y no solo por imposición externa del currículo. En consecuencia, la organización de un medio didáctico apropiado es uno de los cambios más relevantes para desarrollar una enseñanza de ese tipo.

Los recorridos de estudio y de investigación

En toda situación de enseñanza emerge un sistema didáctico formado por los estudiantes, uno o más profesores y el objeto de estudio. En el paradigma monumental hay un único profesor y el saber está determinado de antemano, mientras que en el PCM se estudia una pregunta Q0 denominada generatriz. El proceso de estudio de una cuestión requiere generar un medio didáctico que contenga las herramientas necesarias para elaborar la respuesta, tales como:

• un conjunto de preguntas derivadas, que surgen a partir de la pregunta generatriz y la complementan
• un conjunto de respuestas etiquetadas, llamadas así porque son respuestas reconocidas como tales en una institución y que se pueden encontrar en un libro, la web, el curso de un profesor, etc. El grupo de estudio debe deconstruir y construir las respuestas y evaluar si ellas son relevantes o “válidas”.
• un conjunto de praxeologías, saberes que se utilizan como herramientas —matemáticas o no— para estudiar las respuestas etiquetadas y construir la respuesta a Q0. Por ejemplo, teorías y experimentos.

En un REI, el estudio de un cierto saber depende de cuán necesario es para elaborar una posible respuesta a la pregunta generatriz. La respuesta se produce bajo determinadas condiciones y restricciones a las cuales está sujeta. Es decir, no existe una respuesta universal ni universalmente efectiva (Chevallard, 2009).

En síntesis, el medio didáctico en un REI no está definido de antemano, sino que se construye mientras se elaboran las respuestas y su desarrollo no es exclusivo del profesor, sino que es, además, una responsabilidad de los estudiantes. Ellos pueden incorporar a él cualquier instrumento y herramienta que consideren pertinente y posiblemente útil.

Modelo epistemológico de referencia y recorridos realizados

El modelo epistemológico de referencia [MER] (Chevallard, 2013) es una reconstrucción de todos los saberes involucrados en el problema, realizada por los investigadores. El MER es dinámico y flexible. Se desarrolla y se readapta permanentemente.

El REI se centra en responder Q0: “¿Por qué se cayó la piedra movediza [PM] de Tandil?”. La PM era una “roca oscilante” de granito de 248 toneladas, ubicada al borde de un cerro a 300 m s. n. m., en la ciudad de Tandil, Argentina (figura 1). El atractivo de la PM era que oscilaba cuando se realizaba un torque externo en un lugar apropiado y con una frecuencia justa, propia del sistema PM (Holmberg, 1912). El 29 de febrero de 1912 esta piedra cayó al precipicio. Por más de 100 años se han generado todo tipo de conjeturas, mitos y leyendas. La figura 2 muestra el cerro después de la caída. La cruz roja indica el lugar donde antes se encontraba apoyada la PM.

Si la PM se considera como un sistema oscilante, el estudio se dirige a las oscilaciones mecánicas, para comenzar por modelos relativamente simples como el resorte o el péndulo ideal. Se utilizan sistemas sin rozamiento, en los que la única fuerza en acción es la fuerza de restauración que depende —para oscilaciones de pequeña amplitud— de la forma lineal respecto a la posición de equilibrio. Este modelo se conoce como oscilador armónico simple, cuyo movimiento, a través de las ecuaciones de Newton, se describe mediante una ecuación diferencial lineal de segundo orden y la solución es una familia de funciones armónicas —seno y coseno—. Si se toma en cuenta el rozamiento, es necesario añadir un término ligado al amortiguamiento a la ecuación diferencial, que incluye la primera derivada de la posición —velocidad—. Luego, es posible estudiar sistemas que, además de ser amortiguados, están bajo la influencia de una fuerza externa —forzados—. En el caso de que la fuerza externa sea periódica y su frecuencia sea aproximadamente igual a la frecuencia natural —libre de fuerzas externas— del sistema oscilante, se produce un máximo en la amplitud de oscilación, lo que genera el fenómeno conocido como resonancia mecánica.

Figura 1

Fotografía de la PM

Nota: tomada del Archivo General de la Nación Argentina.

Figura 2

Fotografía del cerro luego de la caída de la PM

Nota: tomada del Archivo General de la Nación Argentina.

Si se considera un cuerpo giratorio suspendido, en lugar de una masa puntual, es preciso estudiar el torque y el momento de inercia de un cuerpo oscilante. Aquí, nuevamente el sistema es lineal para oscilaciones de pequeña amplitud. También se pueden considerar los casos amortiguados y forzados, que corresponden al mismo modelo matemático, pero los parámetros tienen una interpretación física diferente. Sin embargo, este modelo físico —péndulo físico— no es adecuado para el sistema de la PM, ya que se trata de un cuerpo suspendido y la PM estaba apoyada. Esto conduce a la mecánica de los sólidos rígidos oscilantes apoyados. Así, se puede considerar un modelo tipo “mecedora” en el que la base de la PM es curva y se encuentra sobre una superficie plana. En este caso, la oscilación —amortiguada y forzada— está relacionada con un movimiento de roto-traslación (Otero et. al., 2017; Otero et. al., 2017). La aplicación de las leyes de Newton a este modelo conduce a una ecuación diferencial donde los parámetros son específicos de la PM, que viene dada por la siguiente ecuación:

(1)

La solución estacionaria de esta ecuación es: φ(t) = φM cos(wt-ψ), siendo la amplitud y la fase .

El máximo de φM es para . Se deben estimar los parámetros: M0 —torque externo—, I —momento de inercia—, w0 —frecuencia natural de oscilación del sistema— y γ —coeficiente de amortiguación—. Datos detallados sobre la forma, las dimensiones y posición del centro de masas de la PM están disponibles después de la construcción de una réplica (Peralta et al., 2007). Estos datos brindan la posibilidad de estimar algunos parámetros de nuestro modelo como la masa, momento de inercia y la distancia de 7,1 m, a partir de la cual el torque externo podría ser ejercido eficientemente por hasta cinco personas para comenzar la pequeña oscilación. Al usar estos valores, es posible estudiar el comportamiento de la función en función de φM(w) en un rango de frecuencias entre 0,7 Hz y 1 Hz —históricamente reconocidas como las frecuencias de oscilación natural de la PM (Rojas, 1912)— y calcular para cada caso la máxima amplitud φM(wM).

La piedra caería si φc ≤ φM(wM), siendo φM(wM) = M0/(M0I γ) Si γ es muy pequeño —como

se cree es en este caso—, es posible desestimarlo desde , lo cual lleva a wM = w0. Al usar esta aproximación en la ecuación correspondiente a la función amplitud, la condición de caída se vuelve φC = M0/(M0I γ). El valor puede determinarse mediante un análisis de estabilidad elemental, según las dimensiones de la base de la PM (Otero et al., 2017). En este modelo γ es un parámetro libre, para el cual establecemos ad hoc un orden de magnitud de γ ≥ 10-2. Aquí encontramos varias situaciones, que comprenden diferentes pares dentro del intervalo de frecuencias mencionado, que soportan la superación del ángulo crítico, es decir, la predicción de la caída.

Finalmente, se busca una aproximación más apropiada del modelo físico para el amortiguamiento —que claramente no se debe al aire— y se propone un modelo más sofisticado de la piedra como un sólido deformable, donde el contacto en la base —que consideramos una superficie plana— no es un punto, sino un extensión finita, sobre la que se distribuye la fuerza normal, que es más grande en la dirección del movimiento y genera una resistencia a la rodadura, que se manifiesta a través de un par contrario al movimiento. La resistencia a la rodadura depende de la velocidad de la piedra. Esto permite dar una interpretación física del término de amortiguación. Por lo tanto, la física subyacente al amortiguamiento es la misma que hace que una rueda de neumático que rueda horizontalmente en la carretera se detenga. No obstante, en el caso de la piedra, la deformación es mucho más pequeña. Aunque el modelo de “mecedora” deformable tiene parámetros adicionales libres, los valores tabulados del coeficiente de resistencia a la rodadura para piedra sobre piedra —disponibles en la literatura especializada— nos permitieron estimar y justificar los valores de amortiguación que incorporamos ad hoc en el modelo de sólido rígido PM.

La figura 3 presenta un diagrama que sintetiza tanto el MER como los recorridos efectivamente desarrollados durante las cinco implementaciones. El vínculo web que está en la nota permite acceder a una versión en línea de este diagrama. Los nodos que representan cada implementación Iq tienen un enlace que dirige al lector a un archivo que contiene tablas diseñadas para describir los elementos del medio didáctico en cada clase, como se describe en la sección siguiente.

Figura 3

Esquema de posibles recorridos

Nota: disponible en https://cmapscloud.ihmc.us/viewer/cmap/1T074Y5WP-27SKX44-3GX

Metodología

La investigación es cualitativa, exploratoria, descriptiva y de carácter etnográfico (Hernández et al., 2014). Se realizaron cinco implementaciones en cursos regulares de matemáticas que estuvieron a cargo de un profesor del equipo de investigación, en tres escuelas secundarias diferentes del partido de Tandil, Argentina. Estas escuelas fueron seleccionadas intencionalmente con el propósito de que los cursos para desarrollar el REI fueran heterogéneos. La pregunta generatriz del REI es “¿por qué se cayó la PM de Tandil?”. Esta pregunta está estrechamente vinculada al hábitat de los estudiantes, puesto que se trató de un hecho muy significativo y de gran trascendencia en la ciudad, que sigue vigente en la actualidad.

En la investigación participaron un total de N=116 estudiantes de sexto año que tenían entre 16 y 19 años. Las dos primeras implementaciones, I1 e I2 —N1=36, N2=32 estudiantes—, se realizaron en una escuela pública de gestión privada. Cada una duró 11 encuentros. Las implementaciones I3 e I4 —N3=13, N4= 19 estudiantes— se realizaron en una escuela pública rural durante 19 y 17 encuentros respectivamente. La última, I5 —N5=16 estudiantes—, se desarrolló en una escuela pública suburbana en 17 encuentros.

En relación con la gestión del REI, en todas las implementaciones el profesor presentó la pregunta generatriz Q0 el primer día. Los estudiantes debían elaborar una respuesta, para lo cual necesitaron formular preguntas derivadas y responderlas con el estudio de las matemáticas y la física pertinentes. El profesor proporcionó:

• publicaciones realizadas en diarios de la época y otros recientes.
• el libro La piedra viva (El Hage & Levy, 2012), que contiene una recopilación histórica, social, económica y cultural de la ciudad de Tandil, y también una descripción y un análisis detallado de las principales conjeturas acerca de la caída de la PM
• la publicación titulada “¿Cayó o la derribaron?” de la Revista Caras y Caretas (Holmberg, 1912), en la cual el autor realiza una estimación del ángulo máximo de oscilación de la piedra.
• el libro La piedra muerta de Rojas (1912)
• dos textos relativos a los conocimientos específicos: oscilaciones mecánicas y funciones armónicas, elaborados por miembros del equipo de investigación (Gazzola, 2018).
• Applets —physlets— creados por el equipo de investigación y otros disponibles en internet.

Cada encuentro terminó con una socialización donde cada grupo comunicaba sus respuestas. Durante el REI, se realizaron síntesis parciales escritas y luego una síntesis final escrita que incluía las preguntas formuladas, sus respuestas, los conocimientos estudiados y la respuesta final que cada curso consideró como la más apropiada para Q0.

Durante las clases se realizó observación participante y se obtuvieron todos los protocolos escritos de los estudiantes. Al final de cada encuentro, el profesor investigador retiraba las producciones escritas, las digitalizaba y las devolvía en el encuentro siguiente. Además, el profesor llevaba un diario con notas de campo, que se utilizaron de manera complementaria.

Se construyó una tabla 1 que utiliza los componentes del medio didáctico: preguntas derivadas, respuestas etiquetadas y saberes estudiados, para cada encuentro en cada implementación. La primera columna corresponde al número de la clase Cqm, donde 1≤q≤5 corresponde al número de implementación y 1≤m≤nq al número de clase con nq= número total de clases de la implementación Iq. La segunda columna contiene las preguntas estudiadas en esa clase —Qi—. La tercera muestra las respuestas a esas preguntas —Ri— reconstruidas por el grupo de estudio. La última columna se refiere los saberes estudiados —Oj— en el proceso de elaboración de esas respuestas.

Tabla 1

Tabla general de análisis de la mesogénesis clase a clase en I.

Implementación __
Sistema didáctico
Cqm	Preguntas derivadas Qi	Respuestas “etiquetadas” Ri	Saberes Oj

Las tablas permiten describir de manera detallada como se gesta el medio —mesogénesis— en cada implementación. Se puede acceder a ellas a partir del vínculo web que se encuentra en la nota de la figura 3. En la siguiente sección describimos las principales características.

Caracterización del medio didáctico en cada implementación

En todas las implementaciones, se comenzó por los documentos detallados en la sección anterior que propuso el profesor. En principio, estos son medias que potencialmente podrían formar parte del medio. En todos los casos, el grupo de clase optó por los documentos relacionados con una respuesta científica que explicara la caída a partir del fenómeno físico denominado resonancia mecánica. En consecuencia, la publicación del reconocido naturalista de la época (Holmberg, 1912), aparecida inmediatamente después de la caída, fue incorporada al medio. Explicar el movimiento de la piedra y su caída mediante las oscilaciones mecánicas cuestiona las ideas de los estudiantes, que provienen del imaginario social según el cual la piedra tenía un “movimiento perpetuo”. Inicialmente, los estudiantes no conciben que un reducido grupo de personas pudo poner a la piedra en movimiento e incluso ocasionar su caída. Por esta razón, los estudiantes formulan diversas preguntas que conducen al estudio de las oscilaciones mecánicas —armónicas, amortiguadas, forzadas y resonantes— y su caracterización matemática (figura 3). Esto llevó a “dejar de lado” transitoriamente la pregunta generatriz para enfocarse en estos conocimientos específicos, y a retomarla más adelante. En una enseñanza por REI, este gesto de estudio se denomina entrar y salir del tema, porque es preciso estudiar las preguntas derivadas de Q0, que requieren salir de un tema, para estudiar otro que es útil y luego reingresar (Gazzola et al., 2020, 2019).

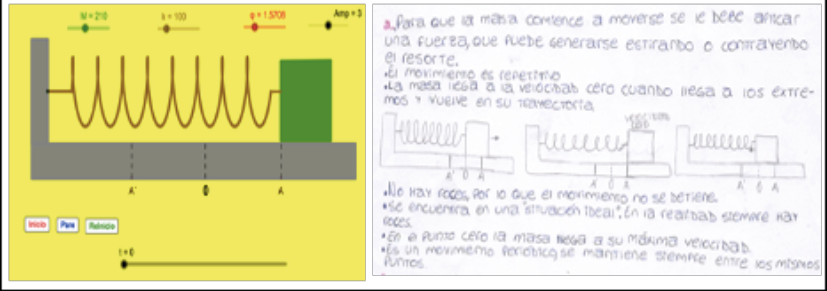
La primera pregunta derivada fue “¿qué son y qué características tienen las oscilaciones?” y su estudio conllevó una salida a la física. En las implementaciones 1 a 3, el profesor propuso un texto con explicaciones, ejemplos y un conjunto de tareas. Se estudiaron los sistemas masa-resorte y péndulo ideal (figura 4) y las principales características del movimiento armónico simple [m. a. s.], las nociones de período, frecuencia, ciclo, la cinemática y la dinámica de este movimiento.

En las implementaciones 4 y 5, el m. a. s. se estudió con un applet GeoGebra sobre el resorte horizontal, que se muestra en la figura 5 junto con el protocolo del estudiante A75.

En todas las implementaciones, el profesor propuso una tarea que proporcionaba las representaciones gráficas posición-tiempo, velocidad-tiempo y aceleración-tiempo para el m. a. s. y solicitaba analizar la variación de dichas magnitudes en el tiempo y las funciones respectivas. El estudio físico del m. a. s. en la clase de matemáticas conduce a preguntarse “¿cómo se describe matemáticamente este movimiento?” y “¿qué características tienen las funciones armónicas?”. Esto implicó una “salida” hacia la matemática. Para estudiar estas funciones, el profesor propuso un documento sobre f(α)=sen(α) y g(α)=cos(α) y sus características —dominio, imagen, período, máximos y mínimos, intervalos de crecimiento y decrecimiento, conjuntos de positividad y negatividad—. Dichas nociones cobraron sentido porque fueron interpretadas a partir del sistema masa-resorte, en el ámbito de lo que Chevallard (2017) denomina matemáticas mixtas. A continuación, se volvió a dejar de lado el sistema masa-resorte y se analizaron las familias de funciones f(α) = Asen(Bα + C) + D y g(α) = Acos(Bα + C) + D. Se variaron los parámetros, para regresar luego al ámbito de las matemáticas mixtas como se muestra en las figuras 6 y 7.

Figura 4

Protocolo del estudiante A61

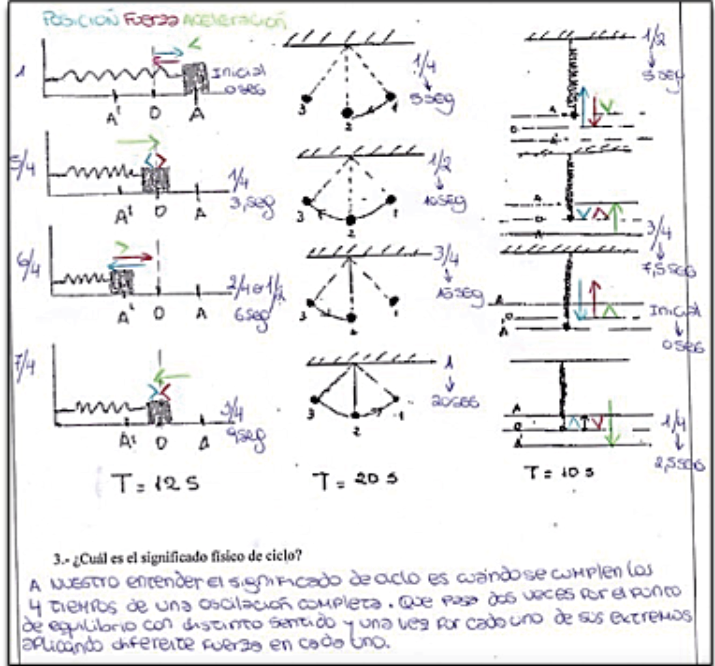
Figura 5

Imagen del applet utilizado y el protocolo del estudiante A61

Figura 6

Protocolo del estudiante A33

Figura 7

Protocolo del estudiante A51

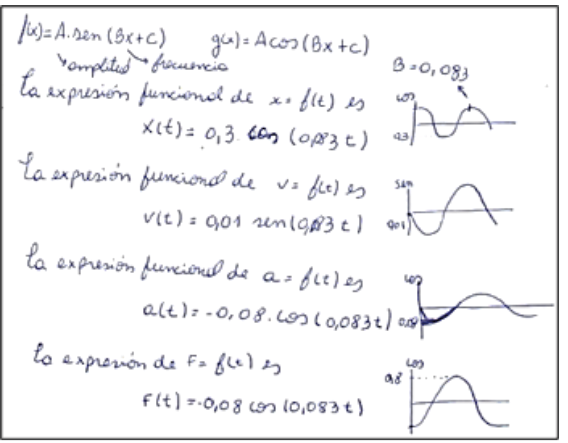
En el ámbito de la física, el profesor propuso analizar la conservación de la energía mecánica de un oscilador armónico y el juego de la energía cinética y potencial. En las dos últimas implementaciones, además de analizar cualitativamente la variación, se utilizaron las fórmulas para la energía potencial, cinética y mecánica (figura 8).

Figura 8

Protocolo del estudiante A61

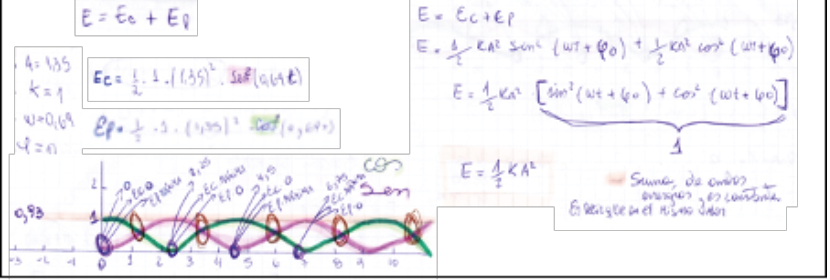
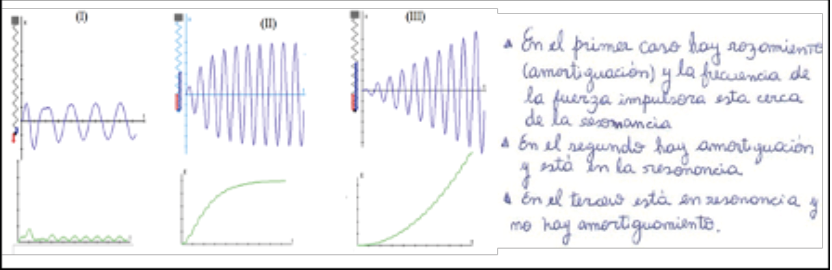
Luego, se retomó la pregunta generatriz y se concluyó que las oscilaciones de la PM no eran armónicas ni perpetuas. De esta manera, se redefinieron los sistemas oscilantes idealizados y quedaron transformados en amortiguados y forzados. Se consideró la no conservación de la energía mecánica en el tiempo, debido a la diferencia de fase de los vectores posición, velocidad, aceleración y fuerza en los distintos tramos del movimiento. Gracias al profesor, se utilizó el sitio interactivo física con ordenador1 y los physlets que permitieron a los estudiantes variar las condiciones iniciales de los diferentes sistemas y describir las representaciones de la posición en función del tiempo y de la variación de la energía en cada uno de ellos. Se consideraron los casos de sistemas sub-amortiguados, sobre-amortiguados y críticos. También se analizaron los sistemas forzados y el fenómeno de la resonancia (figura 9).

Figura 9

Imagen de las simulaciones utilizadas y protocolo del estudiante A17

En las implementaciones 3 a 5, como consecuencia de estar en una clase de matemáticas, los estudiantes preguntaron “¿cómo se describen matemáticamente los sistemas amortiguados y forzados?” y buscaron la respuesta en internet. El profesor debió orientar dichas búsquedas al circunscribirlas a las soluciones de las ecuaciones diferenciales de estos movimientos: φ(t) = φ0 e-t/2γ cos(wt + ψ) , φ(t) = φM cos(wt-ψ) . Nuevamente se realizó una salida a las matemáticas para vincular estas expresiones con los parámetros de las familias de funciones armónicas y para analizar su composición gráficamente, como se muestra en las figuras 10 y 11. Después se vuelve a las matemáticas mixtas y se reinterpretan sistemas oscilantes concretos.

Figura 10

Protocolos del estudiante A86 (a)

Figura 11

Protocolos del estudiante A86 (b)

Para regresar a la pregunta generatriz, el profesor preguntó “¿Qué tipo de oscilación tenía la PM y cómo se producía? ¿Cómo se aplicaría la resonancia a la PM?”. En todas las implementaciones se concluyó que la piedra se trataba de un sistema amortiguado y forzado resonante si era perturbado de manera apropiada por personas. Esta afirmación se profundizó por medio de un experimento en el que se construyó un péndulo con un lápiz, un hilo y una goma de borrar, que permitió observar que al mover el lápiz sobre el borde de una mesa es posible encontrar propioceptivamente la frecuencia del sistema y observar el incremento de la amplitud de oscilación cuando ambas frecuencias coinciden.

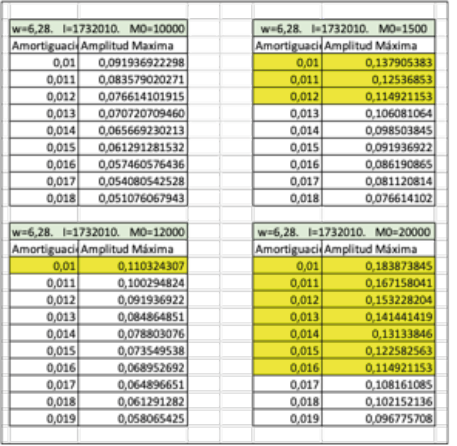
Además, los estudiantes que participaron en las tres últimas implementaciones preguntaron “¿Cuál es la ecuación de movimiento de la PM?”. La respuesta, elaborada por el equipo de investigación (ecuación 1), fue aportada por el profesor. Los estudiantes analizaron cada parámetro de esta función y sus dimensiones: M0 —torque externo—, I —momento de inercia—, w0 —frecuencia natural de oscilación— y γ —coeficiente de amortiguación—; y se preguntaron “¿En qué condiciones habría caído la PM?”. Para esto, calcularon el ángulo crítico de oscilación a partir de una técnica similar a la propuesta por Holmberg (1912), que además tomaba en cuenta los datos morfológicos aportados por el artículo de Peralta et al. (2007). El valor obtenido de θ = 0,11 rad (Otero et al., 2017) se utilizó para analizar la ecuación 1. Se consideró que, si la función amplitud supera ese valor crítico, la piedra se cae por el precipicio. Para los valores de I y de γ, se utilizaron los calculados por los investigadores. Para w0, se adoptó el valor propuesto por Rojas (1912). Se estimó un rango de posibles torques, al considerar que la fuerza podría haber sido ejercida por entre 2 a 5 personas (figura 12).

Inicialmente los estudiantes tuvieron dificultades para comprender que la ecuación ofrece más de una solución e intentaron determinar la cantidad exacta de personas que empujaban la piedra y la fuerza exacta que aplicaron. Entonces, junto con el profesor parametrizaron las funciones (figuras 13 y 14) y encontraron distintas condiciones que configuraban escenarios compatibles con la caída de la PM. Este tipo de tareas interesaron mucho a los estudiantes y son muy infrecuentes en el paradigma tradicional de enseñanza.

Figura 12

Protocolo del estudiante A85

Figura 13

Protocolo del estudiante A81 (a)

Además de realizar todo lo anterior, en la quinta y última implementación, los estudiantes preguntaron: “¿Qué sistema oscilante se ajusta más a la PM?”. Un estudiante de la clase propuso el “caballo mecedor”, que originó la pregunta “¿Cómo era la base de apoyo de la PM?”, lo cual motivó la búsqueda de un modelo que se ajustara a esa base. Esto además motivó a otro grupo de estudiantes a visitar —por iniciativa propia— el parque lítico, donde se encontraba la piedra original y donde está actualmente su réplica. Ellos realizaron un video y tomaron fotos de la réplica y de los pedazos de la piedra esparcidos —llevados a la clase—. Esto propició una nueva discusión en la clase y la elaboración de esquemas, como se muestra en la figura 15. Obsérvese el dibujo de un “triángulo” de base curva como modelo para la base de la PM, en línea con el modelo “mecedora” mencionado antes. Estos modelos solo se consideraron en términos cualitativos, pues no se analizó el movimiento de roto-traslación.

Figura 14

Protocolo del estudiante A81 (b)

Figura 15

Protocolo del estudiante A106

Discusión

En las distintas implementaciones, los estudiantes enriquecieron el medio al formular preguntas cada vez más complejas. Sin embargo, el conocimiento para responder a dichas preguntas fue aportado mayoritariamente por el profesor. En consecuencia, el REI incrementa el papel de las preguntas de los estudiantes, pero no se logró que estos aporten de manera autónoma, a partir de su investigación, el conocimiento para responderlas. Esto sería atribuible a que el paradigma tradicional condiciona la implementación de un dispositivo que es ajeno a él.

En las tres últimas implementaciones, el medio didáctico se enriquece considerablemente al incorporar la caracterización matemática del movimiento de la PM. Se realizaron tareas de análisis y de variación de parámetros y variables, al validar con cálculos —relativamente complejos para este nivel— la conjetura acerca del papel del fenómeno de resonancia en la caída de la piedra. Las tareas matemáticas relativas a la parametrización de funciones mencionadas son completamente ajenas al paradigma de enseñanza tradicional, al igual que la interpretación de las soluciones de las ecuaciones diferenciales en términos del modelo del sistema físico adoptado. Las dificultades de los estudiantes se relacionan con un uso limitado de la noción de función, ya que desconocen el papel de las familias de funciones y de los parámetros. Por ejemplo, ellos esperaban encontrar un único resultado, en lugar de un intervalo de valores posibles compatibles con la caída.

Particularmente, en la quinta implementación, mejoraron tanto el uso de los modelos físicos como su formulación matemática, referidos al sistema de la PM. El modelo de la mecedora, propuesto por un estudiante durante esta implementación fue analizado cualitativamente. La física ligada a la roto-traslación podría tratarse en futuras implementaciones. Las dificultades de los estudiantes en relación con el uso de modelos y de modelización también evidencian su ausencia en la enseñanza tradicional. Por tales razones, no es posible ir más allá del análisis de modelos, cuya caracterización resulta propuesta por el profesor, en estas condiciones.

Al considerar las sucesivas implementaciones, puede apreciarse una mayor participación de los estudiantes en la conformación del medio didáctico. Esto podría atribuirse a decisiones vinculadas al profesor, ya que este no es un estudio longitudinal. Los estudiantes realizaron cada vez mayor cantidad y calidad de preguntas a la vez que el profesor les permitió incorporar al medio sus resultados de búsquedas en internet, documentos de la PM elaborados por ellos mismos e incluso nuevos modelos —como el caso de la mecedora—. Sin embargo, fue el profesor quien estableció en última instancia qué estudiar para responder a cada pregunta formulada.

En todas las implementaciones el profesor debió adoptar una participación mayor a la que se espera en un REI. Por momentos asumió ciertas acciones monumentalistas para hacer funcionar el dispositivo.

Dada la cantidad y variedad de conocimientos y recursos en juego que supone el desarrollo de un REI, tanto para el profesor como para los estudiantes, así como el hecho de que se organiza el tiempo didáctico y el reparto de tareas y responsabilidades de manera muy diferente a la que caracteriza a las clases tradicionales, sería necesario incorporar herramientas como el esquema presentado en la figura 3. Este esquema facilita a todos los participantes el acceso a los componentes del medio didáctico ligados al REI, así como también a los recursos, experimentos y datos que se están utilizando. Además de acceder a todos los recursos compartidos, es posible incorporar nuevos recursos accesibles en línea de manera remota.

Conclusión

En este trabajo se presentan resultados parciales sobre cinco implementaciones de un REI codisciplinar en física y matemáticas, que intenta responder ¿cuáles son los saberes de física y matemáticas principalmente involucrados en el REI y cuáles pueden tratarse en la escuela secundaria? y ¿qué características tiene la construcción del medio didáctico en los recorridos implementados?

La primera pregunta se responde a partir del MER esquematizado en la figura 3. En este desarrollo del REI se estudiaron las oscilaciones armónicas, amortiguadas y forzadas de sistemas ligados a masas puntuales, que resultan heurísticos para considerar sistemas oscilantes de sólidos rígidos y los modelos matemáticos respectivos, fundamentales para el análisis de las soluciones de las ecuaciones diferenciales como funciones parametrizadas. Todo esto no se estudia habitualmente en la escuela secundaria ni en física ni en matemáticas, aunque figura en los programas de dichas asignaturas.

En relación con el medio didáctico, se amplió y se enriqueció progresivamente al considerar todos sus componentes, gracias al carácter codisciplinar de la pregunta estudiada y a las decisiones que el profesor toma basado en la experiencia que adquiere en las implementaciones sucesivas.

Se observan cambios positivos relacionados con la enseñanza monumental, principalmente en cómo los estudiantes enfrentan preguntas desconocidas y buscan respuestas. Finalmente, se destaca el carácter exploratorio de nuestra investigación, que deja preguntas abiertas sobre cómo mejorar la construcción conjunta del medio didáctico en las aulas habituales y sobre el desarrollo de instrumentos como esquemas dinámicos que permiten una actualización permanente de los elementos presentes en el medio y de las preguntas y respuestas que se consideran en el desarrollo del REI.

Referencias

Barquero, B. (2009). Ecología de la modelización matemática en la enseñanza universitaria de las matemáticas [Tesis doctoral, Universidad Autónoma de Barcelona]. Dipòsit Digital de Documents de la UAB. https://ddd.uab.cat/record/63192/

Barquero, B., Ruiz-Munzón, N., Monreal-Galán, J., & Barajas-Frutos, M. (2016). Un recorrido de estudio e investigación sobre la comparación de realidad y previsión de la evolución de los usuarios de Facebook. Revista CIDUI, (3) http://diposit.ub.edu/dspace/bitstream/2445/124582/1/678747.pdf

Chevallard, Y. (2007). Passé et présent de la théorie anthropologique du didactique. http://yves.chevallard.free.fr/spip/spip/IMG/pdf/Passe_et_present_de_la_TAD-2.pdf

Chevallard, Y. (2009). La notion de PER : problèmes et avancées. http://yves.chevallard.free.fr/spip/spip/IMG/pdf/La_notion_de_PER___problemes_et_avancees.pdf

Chevallard, Y. (2013). Enseñar matemáticas en la sociedad de mañana: alegato a favor de un contraparadigma emergente. Journal of Research in Mathematics Education, 2(2), 161-182. https://hipatiapress.com/hpjournals/index.php/redimat/article/view/631

Chevallard, Y. (2017). ¿Por qué enseñar matemáticas en secundaria? Una pregunta vital para los tiempos que se avecinan. La Gaceta de la RSME, 20(1), 159-169.

Costa, V., Arlego, M., & Otero, M. (2014). Enseñanza del cálculo vectorial en la universidad: propuesta de recorridos de estudio e investigación. Revista de Formación e Innovación Educativa Universitaria, 7(1), 20-40. https://dialnet.unirioja.es/servlet/articulo?codigo=5530436

Donvito, A., Otero, M., & Sureda, P. (2014). Actitudes de la pedagogía de la investigación en el marco de la TAD: un análisis en tres escuelas secundarias. Ikastorratza, e-Revista de Didáctica, 12, 1-27.

El Hage, E., & Levy, P. (2012). La piedra viva (2a ed.). Artes Gráficas.

Fonseca, C. (2011). Los recorridos de estudio e investigación en las escuelas de ingeniería. Educação Matemática Pesquisa, 13(3), 547-580. https://revistas.pucsp.br/index.php/emp/article/view/7110

Gazzola, M. (2018). Diseño, implementación y análisis de un Recorrido de Estudio e Investigación co- disciplinar en matemática y física en la Escuela Secundaria [Tesis Doctoral, Universidad Nacional del Centro de la Provincia de Buenos Aires]. Ridaa, UNICEN. https://www.ridaa.unicen.edu.ar/xmlui/discover

Gazzola, M., Otero, M., & Llanos, V. (2019). The characteristics didactic gestures of a Study and Research Path involving mathematics and physics at secondary school. European Journal of Education Studies, 6(7), 491-502. http://dx.doi.org/10.46827/ejes.v0i0.2704

Gazzola, M., Otero, M., & Llanos, V. (2020). Acciones didácticas en el desarrollo de un recorrido de estudio y de investigación que involucra a la matemática y a la física en la escuela secundaria. Perspectiva educacional, 59(1), 52-80. https://doi.org/10.4151/07189729-Vol.59-Iss.1-Art.1006

Hernández, R., Fernández, C., & Baptista, P. (2014). Metodología de la investigación (6ª ed.). McGraw-Hill.

Holmberg, L. (1912). ¿Cayó o la derribaron? Revista Caras y Caretas, 15(702).

Kuzuoka, K., & Miyakawa, T. (2018). Implementing multidisciplinary study and research paths in Japanese lower secondary school teaching. En Proceedings of the 6º Congrès International sur la Théorie Anthropologique du Didactique (pp. 2-18). Autrans.

Oliveira-Lucas, C. (2015). Una posible «razón de ser» del cálculo diferencial elemental en el ámbito de la modelización funcional [Tesis doctoral, Universidade de Vigo]. Repositorio Institucional de la Universidade de Vigo. http://www.investigo.biblioteca.uvigo.es/xmlui/handle/11093/542

Otero, M., Arlego, M., & Llanos, V. (2017). Development of research and study paths in the pre- service teacher education. European Journal of Educations Studies, 3(8), 214-240. http://dx.doi.org/10.46827/ejes.v0i0.883

Otero, M., Fanaro, M., Corica, A., Llanos, V., Sureda, P., & Parra, V. (2013). La teoría antropológica de lo didáctico en el aula de matemática. Dunken.

Otero, M., Gazzola, M., Llanos, V., & Arlego, M. (2016). Co-disciplinary Physics and Mathematics Study and Research Course (SRC) within three study groups: teachers-in-training, secondary school students and researchers. Review of Science, Mathematics and ICT Education, 10(2), 55-78. https://doi.org/10.26220/rev.2315

Parra, V., & Otero, M. (2017). Enseñanza de la matemática por recorridos de estudio e investigación: indicadores didáctico-matemáticos de las “dialécticas”. Revista Educación Matemática, 29(3), 9-29. https://doi.org/10.24844/EM2903.01

Parra, V., Otero, M., & Fanaro, M. (2013). Los recorridos de estudio e investigación en la escuela secundaria: resultados de una implementación. Revista Bolema, 27(47), 847-874.

Peralta, M., Ercoli, N., Godoy, M., Rivas, I., Montanaro, M., & Bacchiarello, R. (2007). Proyecto estructural de la réplica de la piedra movediza: comportamiento estático y dinámico. XX Jornadas Argentinas de Ingeniería. https://jornadasaie.org.ar/jornadas-aie-anteriores/2008/contenidos/resumenes_trabajos/tema_b/051.pdf

Rojas, R. (1912). La piedra muerta. Martín García.

Ruiz, N., Bosch, M., & Gascón, J. (2007). Modelización funcional con parámetros en un taller de matemáticas con Wiris. En L. Ruiz, A. Estepa, & F. García (Eds.), Sociedad, escuela y matemáticas. Aportaciones de la teoría antropológica de lo didáctico (pp. 677- 704). Publicaciones de la Universidad de Jaén.

Sala, G., Barquero, B., Barajas, M., & Font, V. (2016). Què amaguen aquestes ruïnes? Disseny d’una unitat didàctica interdisciplinary per una plataforma virtual. Revista CIDUI, (3). http://hdl.handle.net/2445/114728

Salgado, D., Otero, M., & Parra, V. (2017). Gestos didácticos en el desarrollo de un recorrido de estudio e investigación en el nivel universitario relativo al cálculo: el funcionamiento de las dialécticas. Perspectiva Educacional, 56(1), 84-108. https://doi.org/10.4151/07189729-Vol.56-Iss.1-Art.470

Serrano, L., Bosch, M., & Gascón, J. (2010). Cómo hacer una previsión de ventas: propuesta de recorrido de estudio e investigación en un primer curso universitario de administración y dirección de empresas. En A. Bronner, M. Larguier, M. Artaud, M. Bosch, Y. Chevallard, G. Cirade, & C. Ladage (Eds.), Diffuser les mathématiques (et les autres savoirs) comme outils de connaissance et d’action (pp. 835-857). IUFM de l’Académie de Montpellier.

---