En las carreras de ingeniería se incluyen cursos de cálculo como base para el desarrollo académico de los alumnos y como herramienta para su posterior desempeño laboral. Por ello, el estudio de las dificultades en la formación de ingenieros y, en particular, en el aprendizaje del cálculo se ha convertido en un tema de interés (Bingolbali et al., 2007; Cuevas et al., 2018; Gnedenko & Khalil, 1979; Larios, Páez & Moreno, 2021; Larios, Spíndola et al., 2021; Neubert et al., 2014; Pino-Fan et al., 2018; Romo-Vázquez, 2014).
En este contexto educativo particular, algunos trabajos muestran diferencias entre los estudiantes de diferentes carreras. Bingolbali et al. (2007) muestran que con los estudiantes de ingeniería se privilegia el uso de la derivada vinculada a la noción de cambio, es decir, una concepción física de movimiento; mientras que, para el caso de carreras de matemáticas, el énfasis se pone en una relación gráfica, no física, vinculada con la pendiente de la recta tangente.
Esta diferencia y el hecho de no reconocerla pueden generar anécdotas como la de Giusseppe Peano en su trabajo como docente universitario, quien
no la tuvo fácil con su formalización logicista de las matemáticas. Utilizaba borradores de su Formulario como libro de texto para sus cursos de ingeniería en la Universidad de Turín y se enfrentaba a las quejas de los estudiantes, que avanzaban muy lentamente en la aplicación de las matemáticas, lo que realmente les interesaba como aspirantes a ingenieros. Sus colegas le llegaron a prohibir a Peano dar ciertos cursos debido a su formalismo extremo. (Rojas, 2018, p. 164)
Otros trabajos (Burgos et al., 2021; Larios, Páez & Moreno, 2021; Pino-Fan et al., 2018) estudian la complejidad ontosemiótica de los objetos matemáticos —antiderivada, integral definida y derivada—, así como los significados que los estudiantes les atribuyen en sus prácticas matemáticas. Esto se hace con la intención de establecer una relación entre los significados parciales y el significado holístico de los objetos matemáticos —constituidos por el conjunto de significados parciales desarrollados a lo largo del tiempo—, para así reflexionar sobre las implicaciones en su enseñanza.
Cada significado parcial está vinculado con ideas y nociones existentes en el contexto científico y filosófico en el cual se desarrolla, pues responde a sistemas de prácticas específicos que las personas involucradas tuvieron a la mano, ya sea previamente o por desarrollo propio (Pino-Fan et al. 2011). Esto tiene una gran relevancia en el contexto educativo, porque cada estudiante que ingresa a la carrera de ingeniería ha desarrollado sus propias prácticas matemáticas como producto de su propia formación académica y de su contexto personal y, por lo general, les da más relevancia a algunos significados parciales.
Además, uno de los recursos que influyen más en este proceso de construcción de significados son los libros de texto elegidos por el profesor o por la institución escolar. En ellos se asume una postura con base en los significados atribuidos a los objetos matemáticos que, a su vez, son generados por sus prácticas. El alumno es influido por dichos libros como una parte de su proceso educativo. En este trabajo nos centraremos en estudiar este recurso para identificar los significados parciales del objeto matemático de la derivada en los cursos de cálculo de una y varias variables, por ser uno de los conceptos centrales del cálculo.
En este análisis nos centraremos en los cursos de la Facultad de Ingeniería de la Universidad Autónoma de Querétaro, donde se imparten cursos de cálculo durante el primer año y medio —tres cursos— de la carrera de ingeniería, sin importar la especialidad que se tome. Los dos primeros cursos abordan el cálculo diferencial e integral para funciones de una variable. El tercero se enfoca en el cálculo de funciones de varias variables —funciones reales y vectoriales—.
En cada curso se pueden utilizar libros de texto diferentes, según el curso y el profesor. Un trabajo previo (Sol, 2017) analizó el abordaje que se le daba al tema de límites y, en particular, al tratamiento argumentativo de los teoremas que se presentaban.
Para este análisis, se ha tomado en cuenta un enfoque teórico-metodológico que proporciona herramientas en términos de las prácticas matemáticas que se activan en la exposición de los textos.
Consideraciones teóricas
Se consideraron las herramientas teórico-metodológicas del enfoque ontosemiótico del conocimiento y la instrucción matemáticos (EOS) (Godino et al., 2006; Godino et al. 2007; Godino et al., 2021). En esta perspectiva y desde una visión pragmática, se considera que los significados personales de los objetos matemáticos emergen de las prácticas matemáticas de los individuos cuando se abordan problemas o situaciones por resolver (Godino & Batanero, 1994). Las prácticas matemáticas se componen de acciones —prácticas operativas— y comunicaciones —prácticas discursivas— que el individuo activa para enfrentar situaciones.
Así, en el significado de los objetos matemáticos se considera la relatividad del contexto en el cual son utilizados. Dicho significado puede ser definido como el sistema de prácticas operativas y discursivas que el individuo o la comunidad lleva a cabo para abordar situaciones matemáticas en las que intervienen. Por lo tanto, el sistema de prácticas matemáticas se concibe como todo lo que se puede hacer y decir sobre el objeto matemático.
Ahora bien, las prácticas matemáticas hacen referencia, por un lado, a los significados construidos por el individuo; y por otro, al significado desarrollado y compartido en una comunidad denominada institución. En ese sentido, las herramientas del EOS proporcionan medios para analizar e interpretar, dentro de su complejidad, los procesos didácticos en los que se ponen en juego conocimientos, significados, objetos y aprendizajes en las matemáticas (Godino et al., 2006; Godino et al., 2007).
Para el análisis, en el EOS se considera que los objetos matemáticos no son únicamente los conceptos y los procedimientos, sino:
- las situaciones problemas que se trabajan —tareas, aplicaciones, ejemplos—.
- el lenguaje para la comunicación —verbal/escrito, simbólico, gráfico, tabular, numérico—.
- los conceptos.
- las definiciones.
- las propiedades —teoremas, corolarios, proposiciones—.
- los argumentos —enunciados para justificar o validar propiedades—.
Estos objetos matemáticos primarios se articulan en las configuraciones ontosemióticas (figura 1), que pueden ser configuraciones epistémicas (CE), cuando se hace referencia a los significados y prácticas de una institución —comunidad— de referencia, como es la matemática; o bien, configuraciones cognitivas, cuando hacen referencia a los significados de los individuos (Font & Godino, 2006). Para el análisis de este trabajo, se tuvo en cuenta la noción de CE, al considerar que los libros de textos revisados son tomados como referencia para el desarrollo de los cursos y, por lo tanto, de los aprendizajes y significados de los alumnos de ingeniería.
Figura 1
Representación de la estructura de una configuración ontosemiótica, con sus elementos y las relaciones entre ellos
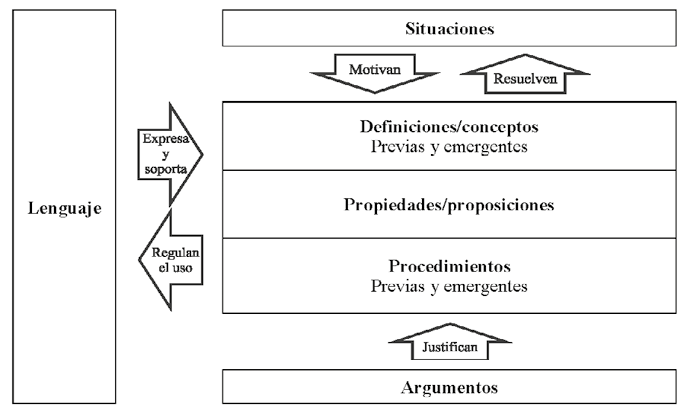
Nota. Tomado de “La noción de configuración epistémica como herramienta de análisis de textos matemáticos: su uso en la formación de profesores” de V. Font & J. Godino, 2006, Educação Matemática Pesquisa, 8(1), p. 69.
Con esta red explícita de relaciones entre los objetos matemáticos, es posible identificar algunos elementos para el análisis (Pino-Fan et al., 2018) y las prácticas matemáticas que se desarrollan en los textos seleccionados, lo cual permite vincular estas prácticas a prácticas matemáticas que corresponden a significados parciales de los objetos matemáticos. En el caso particular de la derivada, Pino-Fan et al. (2011) realizaron un estudio ontológico e histórico, en el que identificaron nueve CE que se corresponden a nueve significados parciales de un significado holístico, compuestos de dichas configuraciones. Como el cálculo es una disciplina científica desarrollada en el seno de comunidades con un desarrollo histórico, las configuraciones y los significados parciales están vinculados a sus respectivos contextos histórico-filosóficos. Además, dichos autores han organizado estas configuraciones según tres problemas genéricos que han interesado a la comunidad científica:
- obtener la recta tangente a una curva.
- obtener los máximos y los mínimos.
- obtener la velocidad de un objeto en movimiento.
Las CE identificadas, en orden histórico, son:
- CE1: prácticas para encontrar rectas tangentes en la geometría, donde se hacen planteamientos particulares para cada tipo de curva, con un lenguaje geométrico y un tratamiento sintético.
- CE2: estudios sobre la variación en la Edad Media, donde se busca estudiar el movimiento de objetos con las herramientas geométricas disponibles —alrededor del siglo XIV—. Se recurre a argumentos geométricos, pero con lenguajes entre descriptivo y geométrico que podían ser confusos, es decir, más extensivos que intensivos.
- CE3: el uso de métodos algebraicos para hallar rectas tangentes, en donde se busca la obtención de rectas normales, tangentes, subnormales y subtangentes a curvas dadas en un punto. Para ello, se utiliza un lenguaje simbólico y con un tratamiento analítico del álgebra y la geometría analítica.
- CE4: concepciones cinemáticas para el trazado de tangentes, donde se aborda el problema del trazado de tangentes a curvas, con procedimientos vinculados con la geometría analítica y el álgebra, pero considerando los puntos como objetos móviles —se “mueven” sobre una curva— y con procedimientos que aún no son generalizables.
- CE5: ideas intuitivas de límite para el cálculo de máximos y mínimos, donde se resuelven problemas prácticos de obtención de máximos y mínimos —alrededor del siglo XVII— con el uso de un lenguaje algebraico, gráfico o descriptivo, que permite la aparición de ideas intuitivas del límite y la derivada, que anteceden a los infinitesimales.
- CE6: uso de métodos infinitesimales en el cálculo de tangentes, donde se utilizan nociones intuitivas de límite, la consideración de las rectas secantes como aproximaciones a la recta tangente y la noción intuitiva de la derivada. Asimismo, se utilizan tratamientos geométricos y algebraicos, con el uso de consideraciones infinitesimales.
- CE7: el cálculo de fluxiones, desarrollado por Newton, considera los infinitesimales, pero, como apuntan Pino-Fan et al. (2011), “enseguida deriva hacia una concepción mecánica, basada en la idea intuitiva del movimiento continuo” (p. 162). Además, dada la aplicabilidad general de los procedimientos que propuso, se considera altamente intensiva.
- CE8: el cálculo de diferencias, desarrollado por Leibniz, incorporó terminología simbólica y procedimientos generales basados en la idea de diferencias infinitesimales y en sumas de infinitamente pequeños, al centrarse en estas cantidades infinitesimales. También se considera que tiene una aplicabilidad general en los procedimientos, por lo que se considera altamente intensiva.
- CE9: la concepción de la derivada como límite, en donde se logra una fundamentación rigurosa a los aportes previos. Así, con argumentos formales y lenguaje simbólico, ocasionalmente apoyado en el geométrico y en procedimientos algebraicos, se tiene una propuesta mucho más intensiva que las anteriores.
Se puede observar que, por la “afinidad” en el tipo de prácticas y en los problemas que las generan, hay tres tipos de configuraciones epistémicas (Pino-Fan et al., 2011):
- relativas a las tangentes —CE1, CE3, CE6 y CE8—.
- relativas a las variaciones y velocidades —CE2, CE4 y CE7—.
- relativas a los límites —CE5 y CE9—.
Es notable cómo el nivel de complejidad semiótica y de abstracción aumenta conforme la historia avanza.
La derivada en los libros de texto
En esta sección se describen las prácticas matemáticas con las que se aborda la derivada en los libros de texto seleccionados y se consideran los significados parciales comentados en la sección anterior. Primero se describen brevemente los textos seleccionados.
Los libros considerados
Los cursos en la formación de ingenieros de la universidad escogida que abordan el estudio del cálculo según funciones de una y varias variables se concentran en el primer año y medio de formación. Estos cursos —semestrales— abordan el estudio del cálculo diferencial y el cálculo integral para funciones reales de una variable real y el cálculo multivariable para funciones de valores vectoriales y funciones reales de varias variables. Particularmente el estudio de la derivada se considera en el primer curso —Cálculo Diferencial— y en el tercero —Cálculo Multivariable—. Para el análisis se seleccionaron cuatro series de libros —en total siete libros de texto— que abarcan lo referente a la derivada en funciones de una y de varias variables:
- Cálculo infinitesimal (Spivak, 2005).
- Cálculo diferencial e integral (Stewart, 1999) y Cálculo de varias variables (Stewart, 2018).
- Cálculo, Tomo 1 (Smith & Minton, 2000) y Cálculo, Tomo 2 (Smith & Minton, 2001).
- Cálculo infinitesimal para estudiantes de ingeniería (Arcos, 2008) y Cálculo multivariable para estudiantes de ingeniería (Arcos, 2009).
Se ha tomado cada serie de libros como una sola unidad, ya que abordan de manera continua el estudio del cálculo.
Configuración ontosemiótica en Cálculo infinitesimal de Spivak (2005). Este texto se usa en el curso de Cálculo Diferencial, en el que se pretende tener una formación formal robusta, según el enfoque del libro. Antes de abordar la derivada, se estudian las propiedades básicas de los números reales, las funciones, la continuidad y los límites. Además, este texto se queda en funciones reales de una variable, por lo que correspondería solo a la parte del primero de los cursos que se imparten. La configuración ontosemiótica de la derivada en este texto aparece en la figura 2.
Figura 2
Configuración ontosemiótica de la derivada de una función de una variable en Spivak (2005)
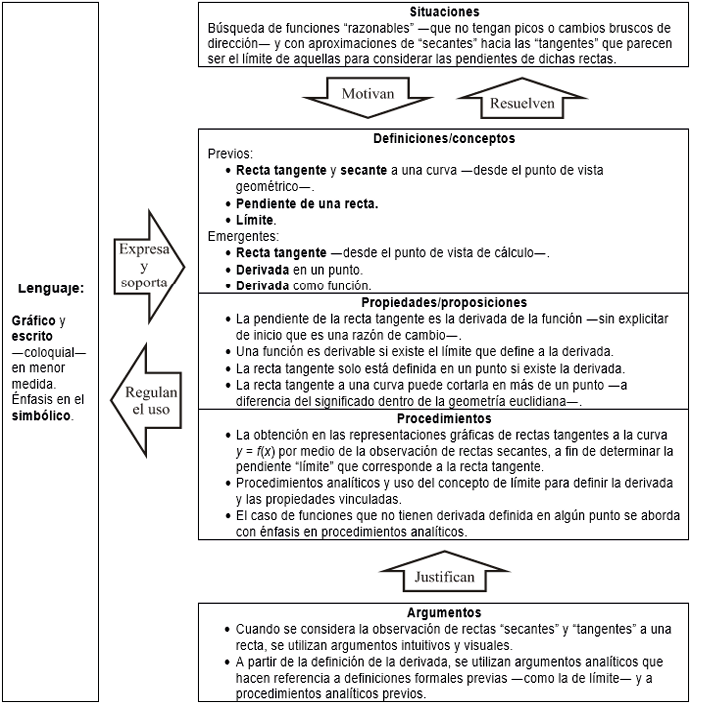
Este texto aborda principalmente el significado parcial final de la derivada, es decir, el que hace referencia a la derivada como límite (CE9), lo cual ocurre a pesar de que pareciera que inicialmente haría énfasis en el significado parcial vinculado con la obtención de rectas tangentes (CE6; CE8).
Tampoco se explicita desde el inicio que la pendiente de una recta, ya sea secante o tangente a una curva, es una razón de cambio. Se le da un tratamiento desde un punto de vista analítico, basado en fórmulas de cursos previos.
Configuraciones ontosemióticas en Cálculo diferencial e integral (1999) y Cálculo de varias variables (2018) de Stewart. Estos textos se abordan en los cursos de Cálculo Diferencial y Cálculo Integral para funciones de una y de varias variables, por lo que se utilizan en los tres cursos. Para este trabajo, se considera la primera parte del primer libro —cálculo diferencial— y el segundo libro —estudio de las funciones de varias variables—.
En su primer libro, Stewart (1999) aborda el estudio de las funciones, el proceso para graficarlas —se incluyen referencias al uso de tecnología digital— y se considera un breve estudio sobre la modelación de fenómenos. También se estudian los límites y la continuidad de funciones antes del estudio de la derivada, pero se mezclan en el mismo capítulo. Se inicia con la exposición de los problemas que dan origen al estudio de la derivada —obtención de tangentes y de la velocidad— y se abordan límites y continuidad, para pasar al estudio de la derivada. La configuración ontosemiótica identificada para la derivada de funciones de una variable aparece en la figura 3.
Figura 3
Configuración ontosemiótica de la derivada de una función de una variable en Stewart (1999)
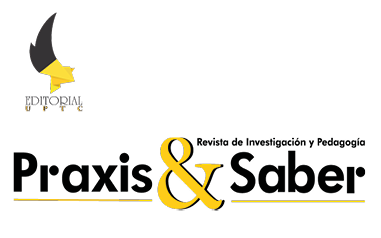
En la primera parte del primer libro, Stewart (1999) declara: “desde el principio, se refuerzan las múltiples representaciones de las funciones: verbal, numérica, visual y algebraica” (p. ix). Esto concuerda con la aproximación que se utiliza.
En el segundo texto (Stewart, 2018), se estudian temas que se consideran antecedentes necesarios para el estudio de las funciones de varias variables. Se abordan las ecuaciones paramétricas y las coordenadas polares. Se retoman las sucesiones y las series infinitas. Se trata el estudio de los vectores en el espacio —propiedades y operaciones—, así como el de las funciones vectoriales y el movimiento en el espacio. En el caso de las funciones de varias variables, antes de la derivada se estudian los límites y la continuidad de estas funciones.
Con lo anterior quedan las bases para abordar el tema de la derivada —parcial y direccional—, cuya configuración ontosemiótica aparece en la figura 4.
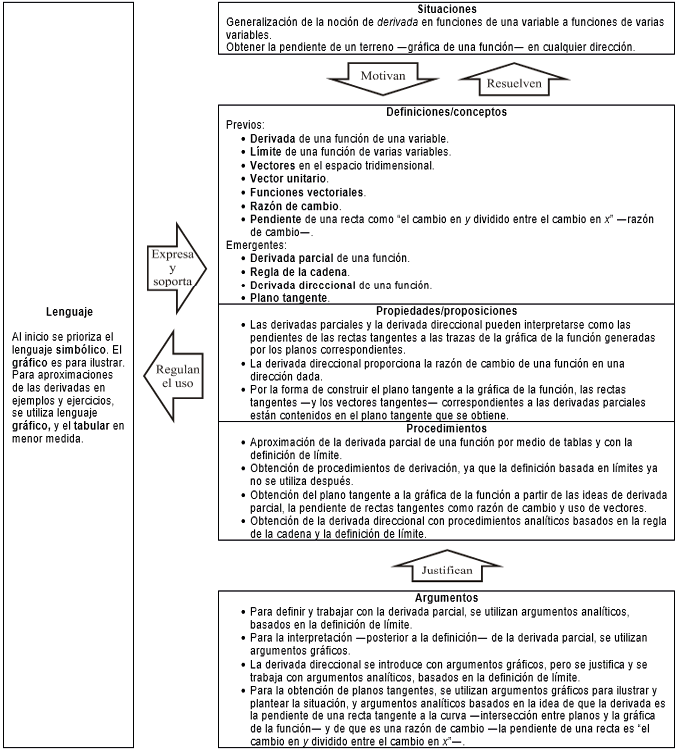
Figura 4
Configuración ontosemiótica de la derivada —parcial y direccional— de una función de varias variables en Stewart (2018)
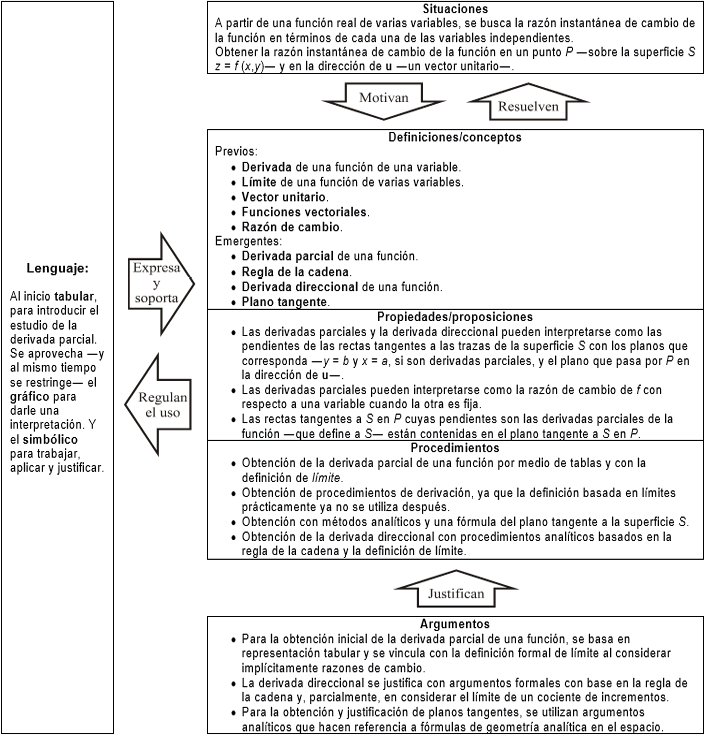
El estudio inicia con funciones de tres dimensiones —dos en el dominio y una en el codominio—, por lo que el trabajo gráfico se centra en lo tridimensional. Se mencionan las funciones de dimensiones mayores en una sección y, por las dificultades para realizar sus gráficas, los ejemplos priorizan funciones de cuatro dimensiones cuyas trazas, de hecho, son tridimensionales y se pueden graficar en el libro. Tal restricción limita el tratamiento y estudio de este tipo de funciones.
El planteamiento de estos textos es que el estudio de la derivada —funciones de una variable— parece surgir de los problemas de obtención de rectas tangentes y de la velocidad de un objeto en movimiento, con apoyo en las representaciones gráficas. Sin embargo, al considerar las configuraciones anteriores, se observó que los textos priorizan el significado parcial de la derivada como límite (CE9), ya que, en sus definiciones y justificaciones, este último objeto matemático es fundamental. Un ejemplo claro es el hecho de que, en el caso de la derivada direccional, no se hace énfasis en la recta tangente a la superficie, sino en la definición de límite como justificación. Las representaciones gráficas funcionan más como ilustraciones.
Configuraciones ontosemióticas en Cálculo, Tomo 1 (2000) y Cálculo, Tomo 2 (2001) de Smith y Minton. Al igual que en el caso anterior, estos dos tomos cubren los tres cursos de cálculo. De manera similar, se revisaron la primera parte del primer tomo —cálculo diferencial— y la del segundo tomo —funciones de varias variables—.
En el primer tomo (2000), Smith y Minton abordan un estudio de temas preliminares —el “capítulo 0”—, que incluye los números reales, el plano cartesiano y las funciones. Ellos vinculan la pendiente de una recta con una razón de cambio: “con frecuencia se describe la pendiente como ‘el cambio en y dividido entre el cambio en x’; se escribe, 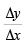 , o más simplemente, Lo que se sube/Lo que se avanza” (p. 13). Además, al considerar triángulos semejantes, aprovechan argumentos geométricos.
, o más simplemente, Lo que se sube/Lo que se avanza” (p. 13). Además, al considerar triángulos semejantes, aprovechan argumentos geométricos.
Luego se introduce la noción de límite, vinculada a esa representación geométrica, como la pendiente de rectas secantes que se acercan a la recta tangente. También se aborda la continuidad de funciones. Antes del estudio de la derivada, introducen los problemas que dan origen a su estudio —obtención de tangentes y de la velocidad de un objeto en movimiento—. En la figura 5 aparece la configuración ontosemiótica identificada para la derivada de funciones de una variable.
En el segundo tomo (Smith & Minton, 2001), se sigue la orientación para las funciones de varias variables, pero antes se abordan temas previos. Se estudian los vectores —propiedades y operaciones— y la geometría del espacio —tridimensional—, así como las funciones con valores vectoriales y cómo pueden modelar el movimiento en el espacio. Al iniciar el estudio de funciones de varias variables, se revisan los temas de los límites y de la continuidad.
Con ello se tienen las bases para abordar el tema de la derivada —parcial y direccional—, cuya configuración ontosemiótica aparece en la figura 6.
Llama la atención que los autores aceptan que es posible graficar funciones con tecnología digital, a pesar de su complejidad. Sin embargo, enfatizan la necesidad de hacer el esfuerzo de graficar a mano:
Usted querrá usar probablemente gráficas generadas por computador en todo este capítulo. Sin embargo, debemos enfatizar en que nuestra meta es la comprensión de las gráficas tridimensionales, lo cual se puede obtener de mejor manera dibujando a mano muchas gráficas. (Smith & Minton, 2001, p. 1021)
Al igual que en el caso del autor anterior, hay un predominio del uso de funciones que permiten gráficas tridimensionales. Incluso hay ejercicios para estimar el valor de la derivada parcial a partir de información organizada en tablas de dos entradas, por lo que funciones de dimensiones mayores no tienen mucha atención.
Por otro lado, con el tratamiento realizado, deducen algunos resultados a través de su construcción. Por ejemplo, para la obtención del plano tangente —y de la fórmula general—, se recurre a las pendientes de las rectas tangentes que se obtienen con las derivadas parciales y a los vectores que generan un plano en el espacio. Así no solo se construye el resultado —que al final se plantea como teorema—, sino que se vinculan los planos tangentes con las derivadas parciales: “para funciones de dos variables, veremos que el plano tangente está determinado por dos pendientes, dadas por las derivadas parciales” (Smith & Minton, 2001, p. 1057).
En este sentido, el planteamiento sobre el estudio de la derivada surge de los problemas de obtención de las rectas tangentes y de la velocidad de objetos en movimiento. No obstante, se hace más énfasis en la noción de razón de cambio, que hace pensar en que se consideran los significados parciales asociados a las configuraciones CE6, CE7 y C8, pero orientados fuertemente hacia la formalización del significado parcial de la derivada como límite (CE9). De hecho, cuando se plantean o se justifican los resultados —teoremas, propiedades, procedimientos— con base en la idea de límite, se continúa principalmente trabajando con estos.
Figura 5
Configuración ontosemiótica de la derivada de una función de una variable en Smith y Minton (2000)
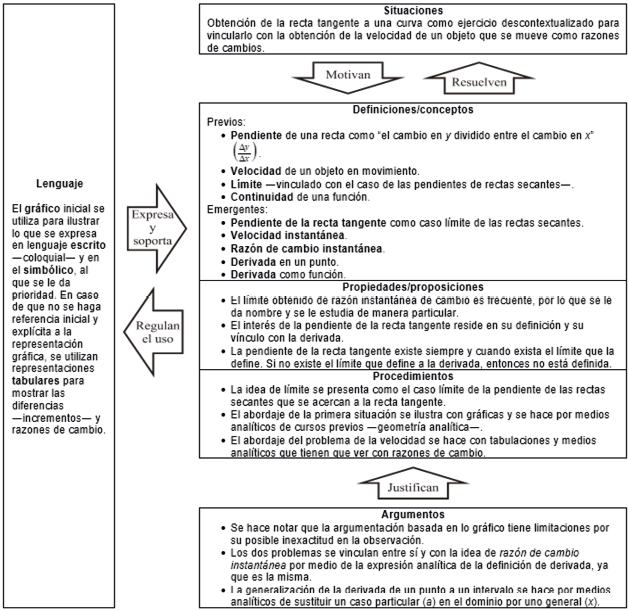
Figura 6
Configuración ontosemiótica de la derivada —parcial y direccional— de una función de varias variables en Smith y Minton (2001)
Configuraciones ontosemióticas en Cálculo infinitesimal para estudiantes de ingeniería (2008) y en Cálculo multivariable para estudiantes de ingeniería (2009) de Arcos. Estos libros abordan el estudio del cálculo para una y varias variables, y cubren los mismos tres cursos de cálculo. Según esta consideración, se revisaron las partes correspondientes al cálculo diferencial y a las funciones de varias variables. Al inicio del primer texto (2008), Arcos plantea su postura con respecto al cálculo:
Hay dos ideas básicas que caracterizan el estudio del cálculo infinitesimal, la primera de las cuales se refiere a la manera en cómo se realizan operaciones aritméticas entre dos cantidades cuando una de ellas es ‘infinitamente pequeña’ con respecto a la otra… La otra idea infinitesimalista es de carácter geométrico, y nos indica que un arco de una curva, comprendido entre dos puntos infinitamente próximos entre sí, puede considerarse como un segmento rectilíneo, es decir, como la cuerda correspondiente al arco. (p. 1)
A partir de ahí, aborda ideas previas relacionadas con el álgebra y la geometría, las series de potencias y el estudio de funciones algebraicas. En cuanto a la noción de límite, no utiliza δ ni ϵ, ya que considera magnitudes infinitesimales que permite una visión intuitiva al respecto.
También se abordan la idea de incrementos, rectas tangentes y razón de cambio. El énfasis se pone en la noción de la diferencial como una diferencia infinitesimal de dos valores de una variable —independiente o dependiente—, y así aborda el problema de obtener la velocidad de un objeto en movimiento. Con ello se inicia el estudio de la derivada, cuya configuración ontosemiótica se presenta en la figura 7.
Figura 7
Configuración ontosemiótica de la derivada de una función de una variable en Arcos (2008)

El vínculo entre la derivada y la tangente aparece casi “forzado”, pues el autor señala las similitudes entre la razón —instantánea— de cambio de la función y la pendiente de la recta tangente a la curva en un punto, ya que la idea de recta tangente a una curva determinada por una ecuación de dos variables se aborda en temas previos.
Con una aproximación como la que presenta el autor, basada en la noción de diferencial, la derivada se convierte en un producto de aquella. De hecho, el segundo libro (Arcos, 2009), orientado al estudio de funciones de varias variables, continúa con esta aproximación. Allí el autor aborda temas relacionados con el espacio tridimensional y lo relativo a ecuaciones paramétricas y funciones vectoriales; también la parte relativa a las trayectorias —curvas— en el espacio como curvatura, estudio del movimiento, longitudes de arco y vectores tangentes. Debido a la aproximación, no utiliza la noción de límite como tal.
Con estos antecedentes se aborda el estudio de la derivada para funciones de varias variables, cuya configuración ontosemiótica aparece en la figura 8.
Figura 8
Configuración ontosemiótica de la derivada —parcial y direccional— de una función de varias variables en Arcos (2009)

Al igual que en los textos anteriores, aunque las definiciones mencionan la existencia de funciones de más de dos variables, el trabajo se centra en funciones que permiten ser graficadas de forma tridimensional y, en ocasiones, se restringe a funciones graficadas en el plano.
En estos textos se han considerado significados parciales asociados a las configuraciones epistémicas CE5, CE6 y CE7, pero que dan prioridad al significado parcial de la derivada del cálculo de las diferencias (CE9), lo cual permite un abordaje más intuitivo y, aun así, fundamentado de los temas.
Comentarios finales
En el EOS se consideran seis facetas en las que se pueden agrupar los elementos que intervienen en el proceso didáctico, pues intervienen aspectos:
- disciplinares —epistémicos—.
- cognitivos —de los alumnos—.
- emocionales.
- interaccionales —entre alumnos y profesores—.
- mediacionales —referidos a los recursos temporales y materiales disponibles—.
- ecológicos —relacionados con el medio ambiente —.
En este trabajo nos hemos centrado en uno de los aspectos que se pueden enmarcar en la faceta mediacional: el libro de texto como recurso didáctico para los cursos de cálculo para ingeniería, en particular en la parte dedicada a la derivada.
En los textos seleccionados se ha mostrado una preferencia por el significado parcial más intensivo disponible, el último desarrollo en términos históricos. Este significado requiere de un nivel de abstracción mayor, con lo que se gana generalización y se “ahorra” tiempo en la enseñanza, a cambio de reducir el tiempo para la intuición de los alumnos. Sin embargo, el desarrollo del individuo se corresponde en cierta medida al desarrollo histórico de la ciencia (Piaget & García, 1998), por lo que se esperaría que los alumnos considerasen de manera más natural un acercamiento acorde con dicho desarrollo histórico. Mochón (1994) comenta algo similar al inicio de su libro:
El cálculo no nació con la idea formal de límite, sino con técnicas más intuitivas basadas en enfoques empíricos. En sus inicios, el cálculo se desarrolló alrededor de lo que podríamos llamar un cálculo ‘discreto’, basado en diferencias. El paso a lo continuo se hizo poco a poco, por medio de elementos algo ideales que representaban porciones infinitamente pequeñas y a los cuales se les denominó infinitésimos. (p. x)
De manera similar, Stewart (Courant et al., 2002) comenta:
Siempre ha habido algo intuitivo y llamativo en los argumentos a la antigua con infinitesimales. Están aún sumergidos en nuestro lenguaje en ideas tales como ‘instantes’ de tiempo, velocidades ‘instantáneas’ y el considerar a una curva como una serie de líneas rectas infinitamente pequeñas y al área acotada por una curva como una suma de una cantidad infinita de áreas de rectángulos infinitesimales. Este tipo de intuición resulta estar justificado, pues se ha descubierto recientemente que el concepto de cantidades infinitamente pequeñas no es deshonroso y no tiene por qué ser descartado. Es posible establecer un marco riguroso para el análisis en el que las definiciones weierstrassianas en términos de épsilon y delta… sean reemplazadas por enunciados sobre infinitesimales, que son increíblemente similares a las ideas intuitivas de Leibniz, Newton y Cauchy. (pp. 563-564)
Según lo anterior —que se refiere a una relación entre aspectos de las facetas epistémica y cognitiva en el EOS— y al considerar el entorno en el que se desarrolla este trabajo —formación de ingenieros, lo cual se enmarca en la faceta ecológica—, se presentan propuestas como las del último grupo de textos, que hacen referencia a una aproximación que considera el análisis no estándar (Arcos, 2008, 2009). En este sentido, Arcos (2019) muestra cómo en los cursos y libros de especialidad de ingeniería se utiliza terminología y aproximaciones que van más cercanas a este tipo de significados de la derivada, por la mayor cercanía a las aplicaciones del mundo físico que tienen los ingenieros.
Así, para el ingeniero, el cálculo y, en particular, la derivada se pueden convertir en una herramienta no solo para modelar, estudiar y prever, entre otros, situaciones o fenómenos que impliquen cambios dinámicos, sino que involucren variables que pueden ser consideradas de manera previa o preventiva, para tomar decisiones apropiadas. Pensemos en un ejemplo típico, una función que modela la deformación de una viga en ingeniería civil, donde el modelo más simple considera tres variables —largo, ancho y alto—, por lo que no puede ser graficada la función en el espacio tridimensional. Además, esa gráfica no representaría a una viga en particular que está cambiando dinámicamente de tamaño, sino que representaría una cantidad infinita de posibles vigas. El individuo debe seleccionar las dimensiones apropiadas de manera previa a la elaboración de la viga. En este punto, pareciera que conviene más considerar a la derivada como una razón de cambio y no como la pendiente de una recta, considerar a la función en su representación tabular más que gráfica y considerar cambios pequeños entre valores, en lugar de intervalos continuos.
En otras palabras, si se privilegia un significado parcial de la derivada, como es el caso de la pendiente de la recta tangente —que a veces se confunde con la recta en sí—, se tiene un desarrollo parcial del significado holístico y se corre el riesgo de que el alumno no construya el significado apropiado. Así, el trabajo que propone Duval (1993) sobre la necesidad de que los alumnos sean capaces de realizar procesos de transformación entre registros semióticos y de conversión en los mismos registros semióticos, de manera eficiente y eficaz, permite representar los objetos matemáticos en el cálculo. De igual manera, siempre está presente el hecho de que las representaciones gráficas están restringidas a ser, a lo mucho, de tres dimensiones, aunque las funciones tengan una dimensión mayor.
Cada vez existe más la posibilidad de que el uso de tecnología digital —los diferentes tipos de software— permita el manejo rápido de cantidades grandes de datos para representar y manejar la información en diferentes registros —gráfico en dos y tres dimensiones, tabular, simbólico—. Así se abre la posibilidad del profesor para ampliar los recursos que puede utilizar. No obstante, el énfasis en algunas de las configuraciones epistémicas de los significados parciales mencionados en este trabajo es un punto que no puede ser olvidado, sin importar la herramienta para el manejo y representación de la información.
Referencias
Arcos, J. (2008). Cálculo infinitesimal para estudiantes de ingeniería. Kali.
Arcos, J. (2009). Cálculo multivariable para estudiantes de ingeniería. Kali.
Arcos, J. (2019). Una presentación de los conceptos del cálculo, en escuelas de ingeniería, no centrada en la definición de límite. El cálculo y su enseñanza. Enseñanza de las Ciencias y la Matemática, 12(1), 46-59.
Bingolbali, E., Monaghan, J., & Roper, T. (2007). Engineering students’ conceptions of the derivative and some implications for their mathematical education. International Journal of Mathematical Education in Science and Technology, 38(6), 763-777. https://doi.org/10.1080/00207390701453579.
Burgos, M., Bueno, S., Godino, J., & Pérez, O. (2021). Onto-semiotic complexity of the Definite Integral. Implications for teaching and learning Calculus. REDIMAT, Journal of Research in Mathematics Education, 10(1), 4-40. https://doi.org/10.17583/redimat.2021.6778
Courant, R., Robbins, H., & Stewart, I. (2002). ¿Qué son las matemáticas? Fondo de Cultura Económica.
Cuevas, O., Larios, V., Peralta, J., & Jiménez, A. (2018). Mathematical knowledge of students who aspire to enroll in engineering programs. International Electronic Journal of Mathematics Education, 13(3), 161-169. https://doi.org/10.12973/iejme/3832
Duval, R. (1993). Registres de représentation sémiotique et fonctionnement cognitif de la pensée. Annales de Didactique et de Sciences Cognitives, 5, 37-65.
Font, V., & Godino, J. (2006). La noción de configuración epistémica como herramienta de análisis de textos matemáticos: su uso en la formación de profesores. Educação Matemática Pesquisa, 8(1), 67-98.
Gnedenko, B., & Khalil, Z. (1979). The mathematical education of engineers. Educational Studies in Mathematics, 10(1), 71-83. https://doi.org/10.1007/BF00311176
Godino, J., & Batanero, C. (1994). Significado institucional y personal de los objetos matemáticos. Recherches en Didactique des Mathématiques, 14(3), 325-355.
Godino, J., Batanero, C., & Font, V. (2007). The onto-semiotic approach to research in mathematics education. ZDM. The International Journal on Mathematics Education, 39(1-2), 127-135.
Godino, J., Burgos, M., & Gea, M. (2021). Analysing theories of meaning in mathematics education from the onto-semiotic approach. International Journal of Mathematical Education in Science and Technology, 0(0), 1-28. https://doi.org/10.1080/0020739X.2021.1896042
Godino, J., Contreras, Á., & Font, V. (2006). Análisis de procesos de instrucción basado en el enfoque ontológico-semiótico de la cognición matemática. Recherches en Didactique des Mathématiques, 26(1), 39-88.
Larios, V., Páez, R., & Moreno, H. (2021). Significados sobre la derivada evidenciados por alumnos de carreras de ingeniería en una universidad mexicana. Avances de Investigación en Educación Matemática, (20), 105-124. https://doi.org/10.35763/aiem20.4002
Larios, V., Spíndola, P., Cuevas, O., & Castro, J. (2021). Conflictos semióticos y niveles de algebrización en aspirantes a Ingeniería. Educación Matemática, 33(3), 263-289. https://doi.org/10.24844/EM3303.10
Mochón, S. (1994). Quiero entender el cálculo. Grupo Editorial Iberoamérica.
Neubert, J., Khavanin, M., Worley, D., & Kaabouch, N. (2014). Minimizing the institutional change required to augment calculus with real-world engineering problems. PRIMUS: Problems, Resources, and Issues in Mathematics Undergraduate Studies, 24(4), 319-334. https://doi.org/10.1080/10511970.2013.879970
Piaget, J., & García, R. (1998). Psicogénesis e historia de la ciencia. Siglo XXI Editores.
Pino-Fan, L., Font, V., Gordillo, W., Larios, V., & Breda, A. (2018). Analysis of the meanings of the antiderivative used by students of the first engineering courses. International Journal of Science and Mathematics Education, 16(6), 1091-1113. https://doi.org/10.1007/s10763-017-9826-2
Pino-Fan, L., Godino, J., & Font, V. (2011). Faceta epistémica del conocimiento didáctico-matemático sobre la derivada. Educação Matematica Pesquisa, 13(1), 141-178.
Rojas, R. (2018). El lenguaje de las matemáticas. Fondo de Cultura Económica; Conacyt.
Romo-Vázquez, A. (2014). La modelización matemática en la formación de ingenieros. Educación Matemática, 26(especial de 25 años), 314-338.
Smith, R., & Minton, R. (2000). Cálculo, Tomo 1. McGraw-Hill Interamericana.
Smith, R., & Minton, R. (2001). Cálculo, Tomo 2. McGraw-Hill Interamericana.
Sol, T. (2017). Análisis de argumentación y demostración en libros de texto universitarios para cálculo diferencial [Tesis de maestría, Universidad Autónoma de Querétaro]. Repositorio Institucional UAQ. http://ri-ng.uaq.mx/handle/123456789/1115
Spivak, M. (2005). Cálculo infinitesimal. Reverté.
Stewart, J. (1999). Cálculo diferencial e integral. International Thomson Editores.
Stewart, J. (2018). Cálculo de varias variables. Cengage Learning Editores.




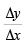 , o más simplemente,
, o más simplemente, 
