Synesthesia and mathematics: a way of life surrounded by representations

Abstract

Frequently and involuntarily, some people perceive sensations from non-corresponding sensory stimuli. This condition is known as synesthesia. The research focuses on the experience of one of the researchers as a synesthete and analyzes the connection between this cognitive trait and the performance in mathematics, regarding the sequence-space synesthesia. The methodology is based on a qualitative approach, through the use of autobiography. Data processing and analysis were carried out through the Atlas.ti software, which allowed the discussion of the theoretical perspective based on the voice of the subject of the study. The study confirms the subjective and idiosyncratic character of synesthesia and recognizes it as a particular representational system that is a favorable condition for the learning of mathematics. However, its applicability in school depends on the teacher’s flexibility to allow for difference and heterogeneity regarding thinking and learning.

Keywords: synesthesia, semiotic representations, mathematical learning, autobiography

Sinestesia e matemática: um modo de vida entre representações

Resumo

Com frequência e de forma involuntária, algumas pessoas percebem sensações de estímulos sensoriais não correspondentes. Esta condição é conhecida como sinestesia. A pesquisa se concentra na experiência de uma das pesquisadoras como sinestesista e analisa a relação entre esta característica cognitiva e o desempenho em matemática, no que diz respeito à sinestesia sequencial-espacial. A metodologia é baseada numa abordagem qualitativa, através do uso da autobiografia. A codificação e a análise de dados foram feitas a partir do software Atlas.ti, o que nos permitiu discutir a perspectiva teórica com base na voz do sujeito de estudo. O estudo confirma o caráter subjetivo e idiossincrático da sinestesia e o reconhece como um sistema representativo particular que é uma condição favorável para o aprendizado da matemática. No entanto, sua aplicabilidade na escola depende da flexibilidade do professor para permitir a diferença e a heterogeneidade de pensamento e aprendizagem.

Palavras-chave: sinestesia, representações semióticas, aprendizagem de matemática, autobiografia

La sinestesia es un rasgo cognitivo en el cual se perciben sensaciones no correspondientes a los estímulos recibidos, como tener sensaciones espaciales al percibir el tiempo o sensaciones de color a partir de determinados olores. Existen alrededor de ochenta tipos de sinestesias, entre los cuales se distingue un grupo denominado sinestesia secuencia-espacio, en el que secuencias relacionadas con el tiempo o los números naturales generan arreglos espaciales visualizados en el espacio peripersonal o en el pensamiento. El sujeto de estudio, que a su vez es investigadora, hace parte del grupo poblacional denominado sinesteta de tipo secuencia-espacio. El estudio responde a la inquietud que vincula el procesamiento y la comprensión de conceptos matemáticos en relación con la percepción sinestésica. En el proceso metodológico, se usa la investigación autobiográfica.

La estructura del escrito se divide en cuatro apartados. El primero corresponde a la contextualización en el campo de la sinestesia, su historia, sus características y sus tipos. En el segundo, se presentan las perspectivas metodológicas adoptadas en la investigación. Se plantea el enfoque investigativo autobiográfico, los momentos de la investigación y estrategias de codificación y análisis mediados por el software Atlas.ti, versión 8.0. En la tercera parte, se presentan apartados de la narración autobiográfica, con el fin de contextualizar al lector en la experiencia del ser sinesteta. En la cuarta parte, se relaciona la sinestesia con la comprensión de nociones matemáticas. Finalmente, se relacionan condiciones emergentes en el rendimiento matemático, a propósito de la sinestesia secuencia-espacio.

Sinestesia: características y tipos

Etimológicamente, sinestesia significa “unión de los sentidos”, del griego “syn” —unión— y “asthesis” —sensación—. Se define como experiencia (Pearce, 2007), como rasgo cognitivo (Day, 2016), como condición neuropsicológica (Simner & Hubbard, 2013) o forma de funcionamiento cerebral inusual (Melero, 2015), en la cual estímulos sensoriales o experiencias cotidianas, como la música o la escritura, suscitan sensaciones adicionales —colores, texturas, formas— que no han sido estimuladas directamente.

El primer caso de sinestesia fue documentado por Georg Tobias Ludwig Sachs en 1812, cuando el término ni siquiera existía. En su tesis doctoral, Sachs hizo una descripción de los colores que él veía con su “ojo de la mente” —mind´s eye— cada vez que pensaba en letras, números, días de la semana u oía notas musicales (Jewanski et al., 2020a; Jewanski et al., 2020b; Simner & Hubbard, 2013). A partir de la descripción de Sachs, la sinestesia fue definida en términos de color y visión.

En 1848, Cornaz dio por primera vez un nombre a esta condición: l´hyperchromatopsie, (Jewanski, 2013). La definió como una anomalía en la visión, en la cual eran vinculadas ideas de color a objetos que no tenían ninguna relación con ellos en el caso de una vista sana (Cornaz, 1851). Posteriormente, Chabalier (1864) decidió cambiar el término por pseudochromesthésie, basado en la conveniencia etimológica, pues, mientras hipercromatopsia se refiere a ver un color en exceso, pseudocromestesia indica una sensación falsa de color. Además, es definida como una facultad peculiar en la cual una sensación primaria o un proceso netamente psíquico evoca una ilusoria percepción de color (Krohn, 1892).

A finales del siglo XIX y comienzos del siglo XX, se utilizaron términos como synopsia (Warren, 1896), psychochromesthesia (Raines, 1909), l’audition colorée (Pédrono, 1882) y sinestesia. Este último fue el adoptado como nombre general para agrupar alrededor de ochenta casos cognitivos relacionados (Day, 2016)1. Asumir el término de sinestesia implicó dejar a un lado la concepción de esta condición en relación con el color y la visión, para empezar a definirla y vincularla con los sentidos.

La percepción sinestésica se caracteriza por ser:

• involuntaria: las sensaciones no pueden ser generadas, manipuladas o suprimidas.
• perpetua: la relación entre un sonido y un color permanece inalterable durante toda la vida, incluso si la persona llega a perder la visión (Pearce, 2007).
• unidireccional: si la letra “A” evoca el color rojo, no implica que el color rojo evoque la letra “A” (Cohen et al., 2009).
• idiosincrásica: las percepciones son particulares en cada sinesteta (Melero, 2015).

En este sentido, la percepción sinestésica difiere de las asociaciones basadas en memoria, como relacionar el color blanco con la nieve (Callejas, 2006), o de la sinestesia metafórica —o metáforas con sinestesia—, la cual es una forma lingüística o figura literaria “en la cual los sentidos se mezclan y entrelazan” (Gaspar, 2007, p. 276), por ejemplo: “escucho con mis ojos a los muertos”2.

La sinestesia es difícil de diagnosticar. Incluso su existencia fue puesta en duda por la psicología experimental, dada la falta de manifestaciones medibles por un observador externo (Cytowic, 2002), que implica un diagnóstico en gran medida dependiente de los relatos del sinesteta. A partir de la creación del Test of Genuineness en 1987, el cual pretende medir la constancia de las percepciones después de un periodo largo de tiempo —especialmente en la sinestesia cuyo concurrente involucra el color—, fue posible determinar con cierta “objetividad” la presencia de la sinestesia (Asher et al., 2006). Sin embargo, dada la cantidad de tipos de sinestesia y su inevitable carácter subjetivo, el diagnóstico aún depende de la información suministrada por el sinesteta.

La sinestesia se clasifica en dos grandes grupos: la sinestesia propia o básica, en la cual el estímulo inductor y la sensación concurrente únicamente involucran los cinco sentidos; y la sinestesia cognitiva, la cual

implica adiciones sinestésicas a los sistemas de categorización cognitiva vinculados a la cultura… Con este tipo de sinestesia, ciertos conjuntos de cosas que nuestras culturas individuales nos enseñan a armar y categorizar de alguna manera específica, como letras, números o nombres de personas, también obtienen algún tipo de adición sensorial, como un olor, color o sabor. (Day, 2016, p. 1)

Como subcategoría de la sinestesia cognitiva, se encuentra la sinestesia secuencia-espacio —sequence-space synesthesia—, la cual agrupa tipos de sinestesia con una experiencia particular (Toomarian et al., 2019). “Algunas secuencias ordinales (por ejemplo, letras, números, días, meses) se perciben en una disposición espacial, de modo que cada miembro de la secuencia induce la sensación de una ubicación muy específica en el espacio” (Jonas & Jarick, 2013, p. 123).

Dentro de la subcategoría de la sinestesia secuencia-espacio, está la sinestesia tiempo, número, espacio —TNS synesthesia—, en la cual “el tiempo y los números son estímulos ‘inductores’, que desencadenan la experiencia ‘concurrente’ de formas espaciales idiosincrásicas en el espacio mental o peripersonal” (Hale et al., 2014, p. 546). Es decir, en algunos casos el arreglo espacial se presenta en una imagen mental; en otros se percibe una proyección en el espacio físico, por ejemplo: “enero puede estar siempre delante de uno a la altura de la cintura de forma que si la persona se gira 90º, enero sigue estando delante de ella” (Callejas & Lupiáñez, 2010, p. 107).

De otro lado, el primer reporte realizado de la sinestesia número-espacio lo realizó Galton en 1880, en su documento Visualised Numerals, donde describe, según sus palabras, personas con el “poder” de ver imágenes en su mind’s eye. En la figura 1, se encuentran algunos casos registrados por Galton (1880), dibujados por los sinestésicos.

Figura 1

Algunos ejemplos de los casos estudiados por Galton (1880)

Ruta metodológica

La investigación se desarrolla con un método cualitativo, puesto que se pretende la construcción de conocimiento a partir de la interpretación de una realidad social particular. Es decir, se intenta captar el punto de vista de quien experimenta y vive dicha realidad (Sandoval, 1996). En este caso, se propuso la construcción de conocimiento acerca de la sinestesia y el aprendizaje matemático por medio de las vivencias narradas por la sinesteta.

Como perspectiva metodológica se adoptó la investigación narrativa, la cual comprende

todos los enfoques y vías de investigación cuya principal fuente de datos se extrae de biografías, material personal o fuentes orales, que dan sentido, explican o contestan preguntas vitales actuales, pasadas o futuras, a partir de las elaboraciones o posibles argumentos con los que se cuentan experiencias de vida o historias vividas desde la perspectiva de quien las narra. (Bolívar & Domingo, 2006, p. 4)

La investigación narrativa busca revelar los acontecimientos y sucesos que determinan la constitución de un sujeto. En ella se entretejen emociones, relaciones, creencias, propósitos y demás dimensiones que comprenden y dan un sentido a la acción humana (Bolívar & Domingo, 2006; Hernández & Rifà, 2011). Además, pretende rescatar la perspectiva subjetiva de la investigación y “alejarse [del] «investigador» como un sujeto abstracto, descontextualizado y con la visión de ojo divino que lo ve todo desde una posición de privilegio” (Márquez et al., 2017, p. 135).

La investigación autobiográfica, como parte de las investigaciones narrativas, se caracteriza por rescatar “las percepciones de la práctica y el conocimiento práctico, experiencial y de vida que son difícilmente perceptibles y transmitidos de otro modo” (Bolívar & Domingo, 2006, p. 5). Busca descubrir “formas de vida, subjetividades, aprendizajes y saberes que habitualmente permanecen fuera de las prácticas que han pasado a ser consideradas e institucionalizadas como «normales»” (Hernández & Rifà, 2011, p. 41). En este sentido, y dado que la sinestesia se caracteriza por ser idiosincrásica —es decir, comprende experiencias sensoriales exclusivas de cada sinesteta—, la investigación asume el método autobiográfico, en donde el investigador es a su vez, el único participante.

Adoptar el método autobiográfico requiere la escritura de la autobiografía que, si bien tiene como propósito la interpretación y la comprensión de una realidad, se configura a partir de su dimensión literaria. En este sentido, la autobiografía consiste en un “relato retrospectivo en prosa que una persona real hace de su propia existencia, poniendo énfasis en su vida individual y, en particular, en la historia de su personalidad” (Lejeune, 1991, p. 48). En ella el autor, el narrador y el personaje son una sola persona.

Se reconocen diferentes tipos de autobiografía, entre ellos:

• las confesiones: predomina la introspección. En la narración imperan las emociones, los sentimientos, las percepciones, e incluso la misma composición del mundo de las ideas del sujeto que recuerda.
• las memorias: se hace un proceso de extroversión. Se enfatiza en los personajes y en el contexto presentes en los recuerdos.
• el autorretrato: se describen los rasgos físicos y psicológicos del autor.
• el diario: se escribe a partir de una cronología de los acontecimientos (Viñao, 1999).

La autobiografía escrita para esta investigación se realizó a manera de confesiones, puesto que se pretendió develar la manera como se percibe el mundo desde una mirada sinestésica y analizar la relación entre la sinestesia y el aprender matemático. En este sentido, si bien en la narración se relacionan personajes importantes en la vida del autor, priman las emociones y los pensamientos que emergieron de cada hecho narrado.

Participantes

La persona sinesteta participante de la investigación presenta sinestesia secuencia-espacio: los números naturales, los meses del año, los días de la semana y las horas del día son percibidos en una secuencia espacial. Presenta agrado y facilidad por las matemáticas y se desempeña como docente en dicha área.

Momentos de la investigación

Preparación y documentación. Se realizó un rastreo documental de libros, artículos y tesis, cuyo objeto de estudio era: sinestesia, sinestesia secuencia-espacio, sinestesia y matemáticas y aprendizaje matemático; de manera que, además de determinar las tendencias y fundamentos teóricos de la investigación, fuera posible construir preguntas orientadoras de la escritura de la autobiografía.

Escritura autobiográfica. En este tipo de investigación, la escritura de la autobiografía es un camino para interpretar, comprender y develar vínculos y relaciones de una realidad, más que una narración de las experiencias del yo (Hernández & Rifà, 2011). La escritura de la autobiografía se configuró en dos momentos: en primera instancia, se realizó una narración autobiográfica a partir de preguntas que determinaron un boceto de ruta que permitiera hacer énfasis en las vivencias relacionadas con la sinestesia y suprimir hechos anecdóticos con poca o nula relación con la condición sinesteta. Las preguntas realizadas fueron las siguientes:

• ¿Cuál es el primer recuerdo que tienes?
• ¿Qué recuerdos tristes o felices tienes de la infancia?
• ¿Cuáles fueron tus sueños de niño?
• ¿Cuándo comprendiste que eras sinesteta?
• ¿Qué anécdotas recuerdas en relación con la sinestesia antes de saber que eras sinesteta?
• ¿Cuáles son las potencias en tu aprendizaje?
• ¿Cuáles crees que son tus dificultades en el aprendizaje?
• ¿Cuáles son las características de tu sinestesia?
• ¿Cómo funciona la sinestesia en tu vida?

En un segundo momento, se leyó el documento que permitió configurar nuevas preguntas, con el fin de aclarar elementos inconclusos, profundizar en la narración de la percepción sinestésica y suprimir apartados de relatos poco relacionados con los objetivos planteados.

Análisis de la autobiografía

El análisis de la autobiografía se realizó en dos partes: la primera sobre una narración en la cual predomina la singularidad de la realidad estudiada. En este caso, el análisis no pretendió encontrar elementos comunes y generalizables, sino que se configuraron “los elementos de los datos en una historia que unifica y da significado a los datos, con el fin de expresar de modo auténtico la vida individual, sin manipular la voz de [la participante]” (Bolívar, 2002, p. 13). Es decir, en primer instancia se tomaron apartes literales de la autobiografía y se organizaron en un relato que pretendió exponer los elementos que configuran el pensamiento sinestésico, en la sinestesia secuencia-espacio.

En un segundo momento, se hizo un análisis de contenido. En el análisis de la información en la investigación autobiográfica, se evita la excesiva categorización y el silencio de la voz autobiográfica. El análisis de contenido “por medio de categorías temáticas, [posibilita] convertir en manejable la información (mediante su reducción) y [permite] su interpretación (mediante la codificación), el procesamiento y la obtención de conclusiones” (Bolívar & Porta, 2010, p. 208).

Este proceso estuvo mediado por el software para análisis de datos cualitativos Atlas.ti, versión 8.0. Se realizó una codificación en vivo y sustantiva, que arrojó un total de 49 códigos diferentes en la revisión inicial. Con este bosque de códigos, se establecieron las relaciones y se agruparon conceptos a partir de sus propiedades sobresalientes. Se buscaron similitudes y diferencias, a fin de convertir dichos códigos en categorías y subcategorías. Producto de esta fase, se obtuvieron 23 categorías y subcategorías diferentes, para finalmente agruparlas en tres categorías principales (figura 2).

Figura 2

Red de análisis definitiva

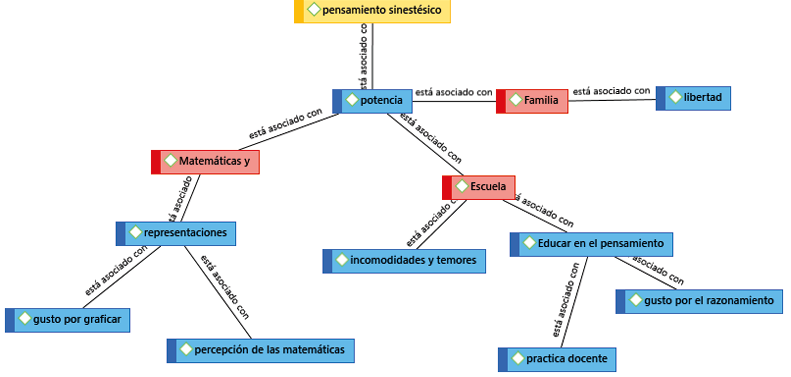
Percepciones sinestésicas en la investigación, una mirada de sí

En el estudio, la experiencia de la sinesteta es el medio para el análisis y el establecimiento de relaciones con el saber matemático. De esta manera, a continuación, se presenta el relato autobiográfico para el caso particular de los números matemáticos.

Conjunto de los naturales en orden sinestésico (relato autobiográfico)

La secuencia de los números naturales, en mi pensamiento, se encuentra en una organización espacial de rectas con vértices en 10, 20, 100, 1000, 10 000, 20 000… (figura 3). A ese espacio voy cada vez que escucho, veo, leo o pienso un número natural. Me es difícil reconocer si puedo visualizar en cada “casilla” el símbolo del número. Lo preponderante en la percepción son los espacios, la gradación en el terreno escalonado. Ver los naturales como secuencia ordenada hace que los postulados de orden me parezcan obvios, pues es absolutamente obvio que el 4 < 8, o que si 2 < 3 y 3 < 9, entonces 2 < 9. Para determinar qué número es mayor que otro, no tengo que pensar en dos conjuntos de elementos y sus cardinales, sino en qué número está “más arriba que otro” en mi secuencia mental.

Figura 3

Fragmento de la secuencia espacial de números naturales —1-10 000—

Para sumar, avanzo en mi secuencia, como dando saltos en un camino empedrado. Por ejemplo, al realizar la suma 58 + 15, voy a mi secuencia mental a la posición del número 58, avanzo 10 puestos y luego 5 (figura 4). Para la resta, en lugar de avanzar, retrocedo; voy hacia atrás. Sin embargo, las sumas o restas de más de tres cifras como 2359 – 1456, no las puedo realizar saltando. Retroceder 1456 puestos no es nada sencillo, por lo que tengo que acudir al algoritmo de restado: poner los números, uno debajo del otro con coincidencia de unidades, decenas, centenas y demás, pero, al restar las unidades, las decenas y demás, utilizo inevitablemente mi secuencia.

La multiplicación depende de los factores. No realizo los saltos de la misma manera para cualquier producto. Multiplicar por dos, por ejemplo, es sencillo, pues es el doble. Los productos dependen inevitablemente de la definición de producto como suma de sumandos iguales. Si pienso en 4 × 3, realizo los tres saltos de cuatro en cuatro de manera rápida y casi imperceptible.

La tabla del siete siempre me ha parecido difícil. No es que no la comprenda, sino que el tiempo que invierto en encontrar el producto es mayor que en las demás. Con 7 × 8, jamás puedo dar una respuesta rápida, instantánea, pues debo pensar en las potencias del 7 y del 8, es decir 49 y 64, para sumar 7 al 49 o restarle 8 al 64.

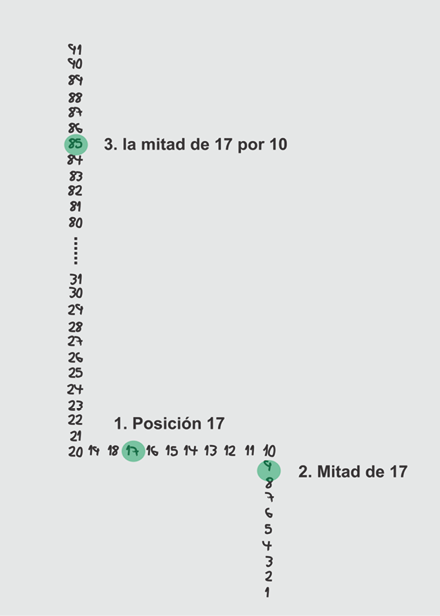
Para multiplicar por cinco, divido en 2 y multiplico por 10, porque en mi secuencia mental es más sencillo encontrar la mitad que multiplicar por 5. Por ejemplo 17 × 5 es 85, puesto que la mitad de 17 es 8,5 (figura 5). Para multiplicar por los múltiplos de 2, regularmente realizo descomposición para que sea más sencillo realizar los saltos, por ejemplo: 14 × 6 = 7 × 2 × 3 × 2 = 7 × 3 × 4 = 21 × 4 = 84.

Figura 4

Adición 58 + 15

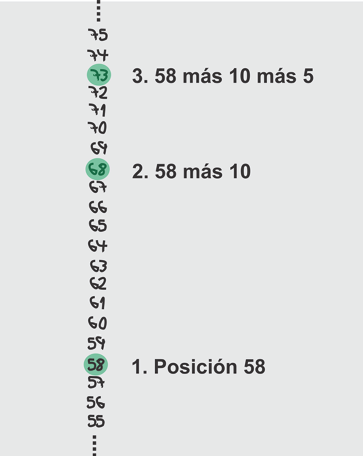
Figura 5

Multiplicación por 5

Además de la secuencia de los naturales, los números pares e impares parecen tener alguna diferencia. Alguna vez mi madre me contó una experiencia en una reunión en la cual le asignaron un número a cada asistente, de manera que se conformaran dos grupos: el grupo de pares y el grupo de impares. Una señora preguntó a mi madre qué era un número par. Mi madre, en lugar de dar una explicación y por la premura del tiempo, le pidió a aquella señora que le enseñara el número. Cuando lo vio, le dijo “es par”. Cuando mi madre me contó, de inmediato pensé y me cuestioné en cómo hubiera explicado a la señora qué es un número par. De una manera sencilla, en mi mente resonaba la frase “un número par es…”. ¿Cómo explicarlo sin mencionar la divisibilidad en ٢?”. Descubrí que dejando a un lado mi sinestesia no era posible. Había que explicar múltiplo y divisor. En un primer momento, pensé que era posible. Pensé que los pares son los pares, aquellos números intercalados con los impares, quizá de alguna manera redondos. Luego, pensé que esa es mi forma de percibir los pares, que si lo explico de esta manera posiblemente será más difícil la comprensión, puesto que es complicado explicar mi sinestesia, eso que sucede en mi mente con los números. Así que imagino la forma de explicar la paridad, es decir, que los pares son aquellos números enteros múltiplos de dos, y por tanto son aquellos terminados en 2,4,6,8 o 0.

El cuerpo de los naturales es un camino en el que transito, avanzo, retrocedo, salto o mido distancias; un camino infinito que tiene una cota inferior. En mi secuencia, la cota inferior no es el cero, sino el uno. Mi camino empieza en el uno, no en el cero. Quizá sea natural, pues el número cero aparece históricamente después de los demás números.

Sinestesia, matemáticas y representaciones

La comprensión de cada concepto matemático requiere inevitablemente el uso de representaciones, pues no existen objetos físicos que puedan ser exhibidos en lugar de símbolos o gráficos (D’Amore, 2009; Duval, 1999). En biología, por ejemplo, es posible observar, tocar, oler y escuchar cualquier animal. Si bien las representaciones de este resultan de ayuda, no son indispensables. En matemáticas, por el contrario, un número, una función y un cuerpo numérico carecen de materia alguna con la cual se pueda percibir a través de los sentidos. Sin embargo, estos conceptos emanan de la realidad. Por ejemplo, la noción de número se funda en la existencia real de unidad y multitudes3, pero, sin la abstracción, el número o cualquier noción matemática no existiría (Gambra, 1996).

Así, las imágenes mentales, al ser evocadas a causa de la sinestesia secuencia-espacio, son un tipo de representación semiótica del cuerpo numérico de los naturales. La sinestesia implica una disposición que favorece el aprendizaje de las matemáticas. Además, si se considera como una condición innata, supone que el sinesteta posee de antemano una representación propia, una forma de “ver” aquello que no existe en el mundo físico. Tiene facilidad de reconocer que los conceptos matemáticos trascienden la experiencia del mundo real y son entes del pensamiento:

Aprendí a sumar con ayuda de granos de maíz. Con ellos armaba los conjuntos que representaban los sumandos y contaba los elementos de su reunión para hallar la suma. Varias tareas las realicé de esta manera, hasta que mis padres sugirieron que era tiempo de que realizara las adiciones mentalmente, sin ayuda del maíz… [Después] descubrí que la sinestesia era fundamental para mi forma de sumar y restar. La adición y la sustracción se fundamentan en mi sinestesia y realizo cada una de las operaciones básicas sencillas a partir de su definición, sin recurrir a la recuperación lingüística de la operación. (Fragmento de la autobiografía)

Es decir la comprensión de adición, por ejemplo, se alcanza al superar la acción de manipular objetos reales —granos de maíz— y abstraer las nociones de número y de operación presente en el material concreto. Esto es, “partiendo de algunos axiomas tan poco numerosos y tan pobres como sea posible en cuanto a su contenido y de algunas definiciones, el matemático elabora, mediante operaciones constructivas, este inmenso universo de relaciones que constituyen los seres llamados abstractos” (Piaget, 1975, p. 65). En el caso de la sinestesia, esta abstracción hace parte de la imagen sinestésica y la imagen sinestésica hace parte de ella. Son una fusión en la cual no es posible concebir una sin la otra.

Alguna vez el profesor de matemáticas de secundaria comentó la importancia de las matemáticas. Quería hacer notar la utilidad de las mismas, evidenciar situaciones en las cuales utilizarlas en el mundo real. Lejos de hablar de cuestiones monetarias, como usualmente suele pasar, habló del orden: “las matemáticas sirven para saber quién es más alto, y por tanto en una fila, no dejar a alguien bajo detrás de alguien alto”. En aquel momento pensé que si esa era la utilidad de las matemáticas, entonces servían para nada, pues no es necesario conocer de matemática avanzada para comparar estaturas. Desde aquel momento solía preguntarme por la utilidad y, más aún, por qué la utilidad en el mundo real sería relevante, pues para mí las matemáticas eran abstractas y en mi pensamiento podía “verlas”, divertirme con ellas. (Fragmento de la autobiografía)

De otro lado, la representación sinestésica de los naturales (figura 3) es insuficiente para la comprensión de conceptos matemáticos como ecuación, función, o sistema de ecuaciones. En otras palabras, estas nociones no podrían ser ejemplificadas o “vistas” en la imagen sinestésica. En consecuencia, el sinesteta encuentra en las gráficas, por ejemplo, un “sustituto” de la representación. Es así como emerge el gusto por graficar, por buscar maneras de visualizar cada concepto matemático, en una inconformidad de utilizar únicamente los lenguajes natural y algebraico como sistema de representación.

Me parecían interesantes los diferentes métodos de solución, especialmente el método gráfico, es decir, saber lo que representa la intersección de dos rectas, visualizar en una gráfica que existe una única solución para un sistema de dos ecuaciones no equivalentes o paralelas, infinitas soluciones cuando son equivalentes y ninguna cuando son paralelas. Solía hacer las gráficas para comprobar el procedimiento algebraico, ya fuera sustitución, eliminación o igualación… Graficar era una de mis actividades favoritas en la clase de matemáticas… La asignatura de Geometría Tridimensional… fue una de las clases más significativas, puesto que se me facilitaba la realización de las gráficas en tercera dimensión. Visualizaba mentalmente, a partir de trazas en los planos xy, xz y yz, la gráfica correspondiente a determinada ecuación. Es así como “veía” los paraboloides, los hiperboloides de una o dos hojas, o la intersección entre dos planos determinantes de una recta. (Fragmento de la autobiografía)

Cada concepto matemático tiene varias representaciones —lenguaje verbal, simbólico, icónico, geométrico, etc.—, que son a su vez objetos matemáticos particulares. La actividad matemática, en gran medida, consiste en reconocer que, si bien una noción matemática comprende un espectro amplio de representaciones, cada una de ellas no corresponde a una noción diferenciada, aun cuando los sistemas de representación resulten absolutamente distantes (Duval, 1999, 2006, 2016; Font et al., 2007). Por ejemplo, el número cuatro puede representarse en los diferentes sistemas, como se ilustra en la figura 6.

Figura 6

Algunas representaciones para el número 4

Además de reconocer que cada una de las representaciones de un concepto, por diferentes que sean, corresponde a la misma noción, el pensamiento matemático exige la habilidad de traducción y conversión entre sistemas de representación (Duval, 2016). En esta habilidad, la sinestesia secuencia-espacio resulta una potencia en la comprensión de las matemáticas, pues el carácter involuntario, automático y aditivo de esta condición permite que, cuando el sinesteta inicia el aprendizaje de las matemáticas, transite de los sistemas de representación simbólicos e icónicos a la representación sinestésica de manera precoz.

Esta trasformación es inconsciente, pero la repetición involuntaria genera que el sinesteta intuitivamente encuentre un atractivo en la transformación de las representaciones y a su vez que le resulte complicado aprender en la ausencia de estas. Por lo tanto, no solo la imagen sinestésica comprendida como objeto matemático sirve en la comprensión de las matemáticas, pues los procesos cognitivos derivados de la sinestesia resultan ser habilidades en bruto de traducción y conversión. De tal manera, la sinestesia secuencia-espacio resulta ser una condición que propicia el pensamiento matemático.

Esa primera clase de topología resultó complicada. Llegué a casa y revisé la definición de la topología usual y sus ejemplos de conjuntos abiertos, con el fin de entenderla. Quizá lo que buscaba era una forma de representarla, de ver mentalmente la topología y sus elementos. (Fragmento de la autobiografía)

Sin embargo, si de producción o resultados se trata, y si se considera la velocidad en el desarrollo de las operaciones fundamentales un elemento sustancial en el aprendizaje, la sinestesia secuencia-espacio, lejos de ser un estado propicio, resulta ser una limitante, pues cuando el proceso de solución de una operación fundamental depende del arreglo espacial producto de la sinestesia, el tiempo requerido para dar respuesta es mayor en sinestetas que en no sinestésicos (Ward et al., 2009; Makioka, 2021).

Si bien entiendo una definición, la velocidad para realizar una operación no es muy alta. Generalmente, los demás realizan determinada operación más rápido que yo. La sinestesia no me ayuda a ser más veloz. Me ayuda a visualizar los conceptos, a ver cada operación, a descomponer números, a ver, por ejemplo, las posibles combinaciones para que una suma sea 20. Me permite además disfrutar de cada proceso. Cuando realizo una multiplicación, además de dar una respuesta, mentalmente disfruto el proceso de llegar a ella. Cada operación que realizo es una oportunidad de deleitar mi mente con una noción matemática. (Fragmento de la autobiografía)

Sinestesia y desarrollo del pensamiento

Si bien se ha mencionado cómo la sinestesia secuencia-espacio, en este caso estudiado4, resulta una potencia para la comprensión de las matemáticas, la sinestesia en sí misma no implica el desarrollo excepcional de habilidades relacionadas con ella ni sobresale como elemento suficiente. En su lugar, es un germen de pensamiento que, sumado a ciertas condiciones escolares y del contexto social, potencia aptitudes y propicia otras condiciones de aprender.

Emergen, entonces, situaciones ajenas a la sinestesia, condiciones sin las cuales la sinestesia en la escuela sería a lo sumo una casualidad, como un rasgo del sujeto impropio al pensamiento análogo, al color de los ojos o al tono de piel. Es decir, si la escuela y el maestro no propician el desarrollo de la curiosidad, la capacidad de indagación, la autonomía, la libertad o el desarrollo del mismo pensamiento, el sinesteta difícilmente podrá reconocer su condición como un elemento esencial de su pensar, como una manera de aprehender y de ver el mundo.

Para Zuleta (1995), el problema de la educación colombiana es la enseñanza en la ausencia de la filosofía, en donde priman los resultados ajenos, el producto, la rapidez y apócopes de esfuerzos, en lugar de los procesos propios y el ejercicio del pensar. En matemáticas, por ejemplo:

[se enseña] que dos más dos son cuatro, que menos por menos da más; el alumno no entiende ni comprende por qué; él solo sabe que si lo hace así resulta y obtiene buenas calificaciones. Mientras uno no sepa por qué menos por menos da más, no hay una apropiación del proceso que conduce a dicho resultado. (p. 12)

Zuleta (1995) propone, entonces, la educación con filosofía, en la cual se resalte y se pretenda formar el pensamiento, enseñar a pensar por sí mismo, en remplazo de “la reproducción de algunas certezas pensadas por otros y mediadas por el maestro. La educación debe desprenderse de dogmas y verdades absolutas” (Pulido, 2012, p. 98). Es decir, el estudiante no acumula información para ser recitada, sino que cuestiona, analiza, reflexiona y discute conceptos.

En este sentido, el maestro de matemáticas, por ejemplo, no debería esperar del estudiante únicamente la reproducción de algoritmos, sino que piense y viva las matemáticas, que sea consciente de lo que hace, por qué y para qué lo hace. El estudiante sinestésico no es ajeno a estas condiciones, pues, si la escuela le anula la oportunidad de pensar, tendrá los mismos vicios y dificultades que los no sinestésicos.

Se me dificultaba comprender la razón de estas propiedades. No identificaba su lógica, por lo que realizar el procedimiento siguiendo únicamente el algoritmo me generaba desconfianza. No encontraba manera además de verificar que el procedimiento estuviera bien desarrollado. En el transcurso de mis estudios universitarios, a partir de la deducción de las propiedades, entendí la razón por la cual se hacía cada una de las operaciones, la razón de cada una de las igualdades. Ahora me parece un tema sencillo e interesante. (Fragmento de la autobiografía)

Por lo tanto, la sinestesia no es una condición con la cual se supriman los problemas educativos, como un estado divino independiente de las prácticas escolares, o un lugar perfecto en el cual el estudiante desarrolla el pensamiento como consecuencia de su rasgo cognitivo particular. La sinestesia en sí misma no es garante de pensamiento. Por ende, es necesaria una educación para el pensamiento, que la fortalezca. Solo de esta manera el sinesteta podrá hacer uso de la sinestesia en sus procesos de aprendizaje.

Educar para el pensamiento requiere abandonar la idea de que entre el maestro y el estudiante hay un sujeto que sabe y otro que no sabe. “El que sabe va a informar e ilustrar al que no sabe, sin que el otro, el alumno, tenga un espacio para su propio juego, su propio pensamiento y sus propias inquietudes” (Zuleta, 1995, p. 12). Es decir, el maestro ha de reconocer que el estudiante tiene sus propias maneras de pensar y de aprender. Más que imponer sus líneas reflexivas, como si existiese un manual generalizado del buen pensar, que el docente posee y al cual los estudiantes han de adecuarse, debe permitir que emerjan y se fortalezcan las rutas del pensamiento propias de cada estudiante. En palabras de Deleuze (2002), el maestro es quien dice “haz conmigo” y no “hazlo como yo”; es decir “se privilegia el aprender sobre el enseñar, pero al mismo tiempo el protagonista es el maestro para completar el sentido de la paradoja” (Pulido & Gámez, 2018, p. 152)

Por tanto, el maestro debe permitir la diferencia, lo heterogéneo en el pensar y el aprender; permitir, por ejemplo, que el estudiante sinesteta piense y aprenda desde su sinestesia (Patiño & Patiño, 2018). Imponer en el sinesteta secuencia-espacio formas de pensar las matemáticas es pretender separar elementos del pensamiento que yacen fundidos en su ser; es pretender relegar y abandonar las propias maneras, las potencias en su pensar.

Recuerdo aprender los números en clase, en la pizarra, y en cambio mi mente me los mostraba con formas y colores, con relaciones personales entre ellos… Los había que se llevaban bien y otros que se llevaban mal. Posteriormente, he caído en la cuenta de que los pares eran las formas blandas, amables (y muy fáciles de sumar, restar, etc., por ser resumibles a 2, yo me entiendo); los impares eran ásperos y puntiagudos… ¡Y los raros! No se lo van a creer… Pero mi mente de niña que no sabía que era un número primo, los veía completamente diferentes. Y todo eso fue borrado gracias a la educación normal, para el orgullo de millones de profesores en este mundo. No se imaginan lo fácil que es hacer operaciones así y, bueno, en general todo. (Irenoula5, 2015, p. 206)

Es decir, la sinestesia secuencia-espacio, o en general cualquier sinestesia, será una potencia para las áreas escolares relacionadas a esta, siempre y cuando el entorno permita el ejercicio del pensar, desde las propias cualidades o maneras de ver el mundo, es decir, pensar desde la sinestesia.

Cawley (2010) afirma que el maestro ha de identificar si sus estudiantes son sinestetas. Propone que se destine tiempo para que se evalúen las formas de percepción; preguntar por la asociación entre letras, sonidos, sabores y colores; monitorear las respuestas para comprobar la persistencia de la asociación en el tiempo; y exponer la sinestesia y sus diferentes tipos, para que el alumno estudie sus percepciones y determine si es sinesteta. El maestro resulta entonces el garante de que las condiciones favorables ofrecidas por la sinestesia tengan fruto. Es decir, un sinesteta sonido musical-color, quien experimenta sensaciones de color al escuchar determinada nota musical, posee aptitudes de músico que deberían ser aprovechadas.

Sería un ideal —o casi una utopía— pretender que el maestro identifique la sinestesia y confugure su interacción en el aula6 para potenciarla, más aún en el contexto colombiano, donde el término resulta desconocido y regularmente se confunde con cinestesia o kinestesia. Incluso, en la colección regional de Colombia de la Scientific Electronic Library Online no se encuentra el vocablo en la categoría de materia. Es pretencioso esperar que el maestro realice tests de aptitudes sinestésicas. Sin embargo, reconocer la forma de percibir el mundo, aun en el desconocimiento de que esta condición recibe en nombre de sinestesia, resulta igual de provechoso, si de potenciar aptitudes se trata. Entonces, más que rotular como sinesteta a un estudiante, el maestro ha de estar atento a sus procesos y “tener ojos para ver, para poder valorar cada acontecimiento singular” (Gallo, 2012).

Sin embargo, ignorar las condiciones de la sinestesia reduce la posibilidad de evitar situaciones de desagrado. Por ejemplo, los sinestetas grafema-color muestran incomodidad e interferencia en sus procesamientos mentales cuando las letras o los números son expuestos en un color diferente al de su percepción (Ghirardelli et al., 2010; Wheeler, 2013; Basirat & Hupé, 2020). Por lo tanto, el reconocimiento de la sinestesia es perentorio para la creación de ambientes seguros y cómodos en el aula (Wheeler, 2013), más que para potenciar las aptitudes sinestésicas.

Conclusiones

La sinestesia es un modo de vida, una forma particular de percibir el mundo y vivir en él, una característica de la investigadora que ha sido aprovechada. Más allá de una anomalía o una extraña condición, la sinestesia es una manera diferente de pensar, de ser y de actuar.

La sinestesia es una experiencia subjetiva, idiosincrásica y de difícil diagnóstico, pues no hay forma de que un sujeto externo observe la percepción sinestésica. Si bien es posible analizar el procesamiento del cerebro cuando se percibe, la percepción en sí —la imagen sinestésica— únicamente puede ser descrita por el sinesteta. Por tal motivo, la investigación autobiográfica permitió develar elementos de la sinestesia secuencia-espacio que desde una visión externa probablemente no hubiesen emergido. Permitió así evidenciar la relación entre sinestesia y matemáticas. Aunque algunos estudios demuestran afectaciones en la velocidad del procesamiento de operaciones fundamentales o correlación entre la sinestesia y el rendimiento de las asignaturas relacionadas a ella, el estudio autobiográfico permitió analizar las razones de dichas afectaciones.

La sinestesia secuencia-espacio favorece el aprendizaje de las matemáticas, puesto que su comprensión depende de representaciones y el sinesteta tiene una tendencia a relacionar y traducir entre diferentes sistemas de representación, ya que, en primera instancia, la imagen sinestésica de los números naturales es una representación de ellos.

El aprovechamiento de estas facultades sinestésicas para el aprender matemático depende de que la escuela se eduque para comprender la diversidad de pensamientos; de que el maestro identifique, permita y respete las maneras de pensar y aprender; de que no imponga sus procedimientos como si fueran los únicos y correctos. Ser sinesteta no es garantía de un buen rendimiento. En algunos casos, la escuela ha sido el espacio en el cual el sinesteta opta por relegar su forma de aprender derivado de la sinestesia y por adoptar maneras ajenas.

Referencias

Aristóteles. (2020). Metafísica. Greenbooks.

Asher, J., Aitken, M., Farooqi, N., Kurmani, S., & Baron-Cohen, S. (2006). Diagnosing and Phenotyping Visual Synaesthesia: A Preliminary Evaluation of the Revised Test of Genuineness (TOG-R). Cortex, 42(2), 137-146. https://doi.org/10.1016/S0010-9452(08)70337-X

Basirat, A., & Hupé, J.-M. (2020). Synesthesia in children with difficulties in written language learning. Consciousness and Cognition, 82, 102951. https://doi.org/10.1016/j.concog.2020.102951

Bolívar, A. (2002). ¿De nobis ipsis silemus?”: Epistemología de la investigación biográfico-narrativa en educación. Revista Electrónica de Investigación Educativa, 4(1), 1-26.

Bolívar, A., & Domingo, J. (2006). La investigación biográfica y narrativa en Iberoamérica: Campos de desarrollo y estado actual. Forum: Qualitative Social Research, 7(4), 1-33.

Bolívar, A., & Porta, L. (2010). La investigación biográfico-narrativa en educación: entrevista a Antonio Bolívar. Revista de Educación, 1, 201-212.

Callejas, A. (2006). Sinestesia y emociones. Reacciones afectivas ante la percepción de estímulos sinestésicamente incongruentes [Tesis Doctoral, Universidad de Granada]. Repositorio institucional (Digibug). https://acortar.link/ehy8E

Callejas, A., & Lupiáñez, J. (2010). Sinestesia temporo-espacial y orientación de la atención. En E. Añaños, S. Estaún, & M. Mas (Eds.), La atención (VI): un enfoque pluridisciplinar (pp. 107-114). Monflorit Edicions i Assessoraments.

Cawley, V. (2010). The Synaesthete: A New Type of “Gifted Student” and How to Teach Them. Procedia-Social and Behavioral Sciences, 7, 574-579. https://doi.org/10.1016/j.sbspro.2010.10.077

Chabalier. (1864). De la pseudochromesthésie. Journal de Médecine de Lyon, (2), 92-102.

Cohen. R., Henik, A., & Walsh, V. (2009). Synaesthesia: learned or lost? Developmental Science, 12(3), 484-491. https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1467-7687.2008.00798.x

Cornaz, É. (1851). De l’hyperchromatopsie. Annales D’Oculistique, 25(1), 3-9.

Cytowic, R. (2002). Synesthesia: A union of the senses. The MIT Press.

D’Amore, B. (2009). Conceptualización, registros de representaciones semióticas y noética: Interacciones constructivistas en el aprendizaje de los conceptos matemáticos e hipótesis sobre algunos factores que inhiben la devolución. Revista Científica, 11, 150-164.

Day, S. (2016). Synesthetes: a handbook. CreateSpace Independent Publishing Platform.

Deleuze, G. (2002). Diferencia y repetición. Amorrortu.

Duval, R. (1999). Representation, Vision and Visualization: Cognitive Functions in Mathematical Thinking. Basic Issues for Learning [Reporte de investigación]. En Proceedings of the Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 1-26). International Group for the -Psychology of Mathematics Education. North American Chapter, Oeri. https://eric.ed.gov/?id=ED466379

Duval, R. (2006). Un tema crucial en la educación matemática: la habilidad para cambiar el registro de representación. La Gaceta de la Real Sociedad Matemática Española, 9(1), 143-168. https://eudml.org/doc/44160

Duval, R. (2016). Un análisis cognitivo de problemas de comprensión en el aprendizaje de las matemáticas. Universidad Distrital Francisco José de Caldas. http://die.udistrital.edu.co/publicaciones/capitulos_de_libro/un_analisis_cognitivo_de_problemas_de_comprension_en_el_aprendizaje

Font, V., Godino, J., & D’Amore, B. (2007). Enfoque ontosemiótico de las representaciones en educación matemática. For the Learning of Mathematics, 27(2), 3-9.

Gallo, S. (2012, 6-8 de febrero). As múltiplas dimensões do aprender [Ponencia]. Congresso de Educação Básica: aprendizagem e currículo. Universidade Federal de Santa Catarina, Florianópolis. Brasil.

Galton, F. (1880). Visualised numerals. Journal of the Anthropological Institute, (10), 85-102.

Gambra, J. (1996). El número en Aristóteles. Thémata: Revista de Filosofía, 17, 45-74.

Gaspar, V. (2007). Metáfora, sinestesia y otras figuras retóricas en El perfume. Historia de un asesino, de P. Süskind. Cultura, Lenguaje y Representación, (5), 273-283. http://www.e-revistes.uji.es/index.php/clr/article/view/1364/1207

Ghirardelli, T., Bergfeld, C., Zilioli, M., Bailey, L., & Kretschmar, P. (2010). Synesthesia Affects Verification of Simple Arithmetic Equations. The Journal of General Psychology, 137(2), 175-189 https://doi.org/10.1080/00221301003645152

Hale, J., Thompson, J., Morgan, H., Cappelletti, M., & Cohen, R. (2014). Better together? The cognitive advantages of synaesthesia for time, numbers, and space. Cognitive Neuropsychology, 31(7/8), 545-564. http://dx.doi.org/10.1080/02643294.2014.967759

Hernández, F., & Rifà, M. (2011). Introducción: investigar sobre el relato de la propia experiencia. En F. Hernández, & M. Rifà (Eds.), Investigación autobiográfica y cambio social (pp. 7-18). Octaedro.

Irenoula. (2015). Desde la experiencia. En M. Merino. Todo sobre el autismo (pp. 195-212). Alfaomega

Krohn, W. (1892). Pseudo-chromaesthesia, or The Association of Color with Words, Letters, and Sounds. American Journal of Psychology, 5, 20-41.

Jewanski, J. (2013). Synesthesia in the nineteenth century: scientific origins. En J. Simner, & E. Hubbard, (Eds.), Oxford Handbook of Synesthesia (pp. 369-398). Oxford University Press.

Jewanski, J., Simner, J., Day, S., Rothen, N., & Ward, J. (2020a). The evolution of the concept of synesthesia in the nineteenth century as revealed through the history of its name. Journal of the History of the Neurosciences, 29(3), 259-285. https://doi.org/10.1080/0964704X.2019.1675422

Jewanski, J., Simner, J., Day, S. A., Rothen, N., & Ward, J. (2020b). The “golden age” of synesthesia inquiry in the late nineteenth century (1876–1895). Journal of the History of the Neurosciences, 29(2), 175-202. https://doi.org/10.1080/0964704X.2019.1636348

Jonas, C., & Jarick, M. (2013). Synesthesia, sequences, and space. In J. Simner, & E. Hubbard, Oxford Handbook of Synesthesia (pp. 123-148). Oxford University Press.

Leguizamón, J. (2017). Patrones de interacción comunicativa del profesor universitario de matemáticas. Un estudio de caso. Praxis & Saber, 8(16), 57 - 82. https://doi.org/10.19053/22160159.v8.n16.2017.6200

Lejeune, P. (1991). EI pacto autobiográfico. Suplementos Anthropos, 9, 47-61.

Makioka, S. (2021). Idiosyncratic spatial representations of the days of the week in individuals without synesthesia. Cognition, 207, 104500. https://doi.org/10.1016/j.cognition.2020.104500

Márquez, M., Padua, D., & Prados, E. (2017). Investigación narrativa en educación. Aspectos metodológicos en la práctica. En S. Rendon & F. Angulo (coords), Investigación Cualitativa en Educación (pp. 133–148). Miño y Dávila.

Melero, H. (2015). Sinestesia, bases neuroanatómicas y cognitivas [Tesis doctoral, Universidad Complutense de Madrid]. E-Prints Complutense. https://eprints.ucm.es/id/eprint/30996/

Patiño, D., & Patiño, O. (2018). Diversidad y aprendizaje: Adición y sustracción en un niño autista. En Ó. Pulido & M. T. Suarez (Coords.), Infancia, Diversidad y Filosofía: Voces, Gritos y Reclamos (pp. 71-89). Editorial UPTC.

Pearce, J. (2007). Synaesthesia. European Neurology, 57(2), 120-124. http://dx.doi.org/10.1159/000098101

Pédrono, L. (1882). De l’audition colorée. Annales d’Oculistique, (88), 224-237.

Piaget, J. (1975). Introducción a la epistemología genética: El pensamiento matemático. Paidós.

Pulido, Ó. (2012). Estanislao Zuleta: educación con filosofía. Cuestiones de Filosofía, 14, 79-99.

Pulido, Ó., & Gámez, Ó. (2018). Aprender, filosofar y vivir: formas y expresiones de la enseñanza de la filosofía en Colombia. En O. Pulido, Ó. Espinel, & M. Gómez (Coords.), Filosofía y enseñanza: Miradas en Iberoamérica (pp. 33-70). Editorial UPTC.

Quevedo, F. (2017). Desde la torre. Fondo de Cultura Económica

Raines, T. (1909). Report of a Case of Psychochromesthesia. Journal of Abnormal Psychology, 4, 249-252.

Sandoval, C. (1996). Investigación Cualitativa. ICFES

Simner, J., & Hubbard, E. (2013). Oxford Handbook of Synesthesia. Oxford University Press.

Toomarian, E. Y., Gosavi, R. S., & Hubbard, E. M. (2019). Implicit and explicit spatial-numerical representations diverge in number-form synesthetes. Consciousness and Cognition, 75, 102806. https://doi.org/10.1016/j.concog.2019.102806

Viñao, A. (1999). Las autobiografías, memorias y diarios como fuente histórico-educativa: tipología y usos. Sarmiento. Revista Galego-Portuguesa de Historia da Educación, 3, 223-258.

Ward, J., Sagiv, N., & Butterworth, B. (2009). The impact of visuo-spatial number forms on simple arithmetic. Cortex, (45), 1261-1265. http://dx.doi.org/10.1016/j.cortex.2009.03.017

Warren, H. (1896). Synaesthesia and Synopsia. The American Naturalist, 30, 689-691.

Wheeler, K. (2013). Understanding Synesthesia and Impact for Learning [Tesis de Maestría, Dominican University of California]. Education Resources Information Center. https://eric.ed.gov/?q=synesthesia+and+education&id=ED542164

Zuleta, E. (1995). Educación y democracia, un campo de combate. Fundación Estanislao Zuleta; Corporación Tercer Milenio.

---