La amplia disponibilidad de medios digitales ha permitido hacer un seguimiento puntual a la evolución de la pandemia de covid-19 a través de los contenidos en sitios especializados, de voceros de organismos mundiales y de autoridades de salud pública. Esta información es un referente importante para la toma de decisiones en el ámbito del cuidado de la salud. No obstante, para acceder a esta información se requieren conocimientos y competencias matemáticas que permitan activar y movilizar a las personas para comprender fenómenos, relaciones, responder preguntas y, en general, actuar apropiadamente en respuesta a los desafíos de las situaciones (Niss & Højgaard, 2019).
A finales del siglo pasado, diversas organizaciones mundiales empezaron a establecer políticas respecto a la importancia de las habilidades aritméticas para hacer frente a las demandas cuantitativas en la vida adulta, bajo el argumento de que el pensamiento matemático es clave para aumentar las oportunidades en la vida después de la escuela (Unesco, 2007), así como un medio poderoso para interpretar y controlar la realidad social (Organización para la Cooperación y el Desarrollo Económicos [OCDE], 2012). En la perspectiva de Lüssenhop y Kaiser (2020), la falta de habilidades de cálculo conduce a serias dificultades en el manejo de situaciones de la vida cotidiana y se convierte en una carga social cuando el individuo no puede afrontarlas; además, suele traer consecuencias negativas para sus aspiraciones profesionales, el manejo de sus finanzas, la participación social y política, entre otros (Geiger, et al., 2015).
Esta fue una razón suficiente para que los organismos internacionales hayan puesto mucha atención a los sistemas escolares, tanto para orientar su organización y definir “lo que debería ser la educación” como para constatar el desempeño académico de maestros y alumnos a través de evaluaciones estandarizadas. De esta forma, la noción de logro educativo, explicado ampliamente por Montecino y Valero (2016), se ha posicionado como uno de los temas centrales en las discusiones sobre calidad de los sistemas educativos, ya que resulta benéfico tanto para los individuos como para la sociedad en la que participan (OCDE, 2014). En esta perspectiva, Niss y Jablonka (2020) señalan que se le ha conferido a la escuela garantizar el desarrollo de una matemática funcional. No obstante, como lo explican Lüssenhop y Kaiser (2020), las matemáticas aprendidas en la escolaridad obligatoria no se transfieren de forma automática a las situaciones de la vida diaria. Por ejemplo, hay evidencia de que una gran parte de los adultos jóvenes tienen bajas habilidades en aritmética (O’Donoghe, 2002), lo cual aumenta su propensión a la vulnerabilidad, especialmente cuando se trata de preservar la salud. De acuerdo con Heilmann (2020), los adultos con un bajo dominio aritmético son 2.5 veces más propensos a reportar una enfermedad o discapacidad.
La aritmética de la salud, como la denominan Gal et al. (2020), es definida como la capacidad de los individuos para acceder, procesar, interpretar, comunicarse y actuar a partir de la información sobre temas de salud, desde aspectos numéricos, cuantitativos, gráficos, bioestadísticos y probabilísticos (Golbeck et al., 2005). Esto exige competencias de cálculo en diferentes niveles de profundidad, de las simples a las avanzadas y, eventualmente, es la base de la toma de decisiones en situaciones específicas, por ejemplo: definir dosis de medicamentos, extraer información relacionada con la salud de los envases de alimentos o comprender los datos estadísticos (Heilmann, 2020). Incluso comportamientos relacionados con el cuidado de la salud —como no fumar, el ejercicio y la adecuada alimentación— están relacionadas con cálculos numéricos e interpretación de datos estadísticos (Gal et al., 2020).
Diversos estudios, como el de Lampert y Kroll (2010), han demostrado que la prevalencia de la salud y la enfermedad no es una cuestión aleatoria: la educación influye en comportamientos más saludables. De acuerdo con el estudio de Cutler y Lleras-Muney (2010), las personas con un bajo nivel de habilidades aritméticas tienen más dificultad para comprender los riesgos en la salud de determinados comportamientos, para cumplir con los regímenes de medicamentos y para controlar los padecimientos crónicos. Heilmann (2020) señala una correlación entre el dominio de las habilidades de cálculo y la condición de salud, lo cual implica que las poblaciones con limitadas competencias aritméticas pueden aumentar su vulnerabilidad, entendida como el riesgo aumentado y/o permanente del deterioro de la salud.
Aunque el reporte nacional del promedio de escolaridad de la población mexicana entre 25 y 64 años (Instituto Nacional de Estadística y Geografía [INEGI], 2018a) indica 9.6 años de escolaridad para 2016, todo indica que las matemáticas aprendidas en la escuela básica no se mantienen ni se recuperan del todo en la vida adulta. Coben y O’Donoghen (2020) afirman que este bajo nivel de habilidades y razonamiento matemático tiene un impacto negativo en la vida adulta, pues está asociado con baja productividad. Al respecto, la OCDE (2014) destaca que las sociedades modernas valoran a los individuos no por lo que saben, sino por lo que pueden hacer con lo que saben. El hecho de saber y dominar conceptos y procedimientos de cálculo no hace necesariamente que una persona sea matemáticamente funcional. La vida diaria exige aplicar matemáticas en diversas circunstancias sociales para responder a problemas inesperados, reflexionar sobre ellos y manejar situaciones con información matemática en diversos contextos; pero, sobre todo, exige juzgar críticamente la información matemática, para identificar manipulaciones y tomar mejores decisiones.
Un punto de referencia sobre esta discusión son los resultados del Programa para la Evaluación Internacional de las Competencias de los Adultos (PIAAC), de la OCDE (2019), el cual tiene como propósito determinar la capacidad de acceder, usar, interpretar y comunicar información e ideas matemáticas para participar y gestionar las demandas matemáticas de una variedad de situaciones en la vida adulta. En su último reporte, posiciona a México en el fondo, con alrededor del 40 % de personas por debajo del nivel 1, en donde se pide llevar a cabo procesos simples, como contar, clasificar, realizar operaciones aritméticas básicas con números enteros o dinero, o reconocer representaciones. Tan solo 11.7 % está en el nivel 3 o superior, donde se pide interpretar información matemática, menos explícita, incrustada en contextos que no son familiares, con representaciones más complejas. En este nivel las tareas requieren la aplicación de sentido numérico y espacial; el reconocimiento de relaciones matemáticas, patrones y proporciones expresadas en forma verbal o numérica; y la interpretación y el análisis básico de datos y estadísticas en textos, tablas y gráficos (OCDE, 2019). Este escenario coincide con otros estudios, como el de Furman (2012), en el que reporta que una gran proporción de los jóvenes en el área de Latinoamérica no pueden reconocer la variable que se mide en un experimento, ni diferenciar el modelo del fenómeno que se modeliza.
Un aspecto importante de las habilidades numéricas es la posibilidad de desarrollar una visión crítica del mundo, lo cual propicia la participación y el empoderamiento de las personas. Sin embargo, este pensamiento crítico no emerge de forma automática después de cursar los programas de estudios. Los sistemas educativos están más interesados en lograr que los alumnos sean exitosos en matemáticas que en el hecho de que las usen como un medio para actuar en el mundo con un compromiso crítico con temas de relevancia social, política y ambiental (Jablonka, 2020). Estudios como este buscan contribuir a la discusión del papel de la escuela en la formación de ciudadanos, particularmente cuando deben afrontar diferentes retos en la vida diaria.
Metodología
El propósito de este estudio es identificar los planteamientos matemáticos en los reportes oficiales y describir las competencias matemáticas que los ciudadanos requieren para acceder a esta información. Esta investigación es de corte cualitativo, pues tiene un carácter descriptivo e interpretativo de las competencias matemáticas, sin pretender generalizar o inferir resultados a partir de una medida estadística. Para establecer la metodología de análisis, se emplearon dos referentes: las habilidades de cálculo desde el contexto de la aritmética de la salud y el constructo de competencias matemáticas.
Para el primer referente se retoma a Heilmann (2020), quien señala que la aritmética de la salud se refiere a todas las situaciones que exigen a las personas emplear sus competencias aritméticas como un medio para la toma de decisiones informadas sobre su salud. Su modelo describe cuatro dimensiones:
- el cálculo básico: incluye la identificación de números y la comprensión de datos cuantitativos.
- el cálculo computacional: involucra el conteo, el cálculo y las manipulaciones numéricas simples.
- el cálculo analítico: incluye dar sentido a la información, comprender las proporciones y porcentajes y comprender gráficos básicos.
- el cálculo estadístico: involucra la comprensión de conceptos y resultados estadísticos, la comprensión de planteamientos probabilísticos, el análisis crítico de la información, la comprensión y la interpretación de gráficos complejos y la toma de decisiones basadas en comparaciones de riesgos (Golbeck et al., 2005).
Los dos primeros niveles, denominados por Heilmann (2020) como habilidades numéricas primarias, se asocian con funcionar matemáticamente en un contexto de salud —por ejemplo, contar o extraer información de un gráfico—. Los dos últimos niveles se denominan habilidades numéricas aplicadas e interpretativas y se asocian con la toma de decisiones basada en una evaluación de riesgos y con la capacidad de manejar información numérica y estadística de forma crítica, incluida la comprensión de métodos y probabilidades. De acuerdo con Gal et al. (2020), el cálculo numérico puede ser visto como una competencia porque tiene la característica de ser dinámico y depende de las condiciones individuales para definir un comportamiento específico. Es decir, está asociado a una acción.
Por otra parte, el término competencia matemática es definido por Niss y Højgaard (2019) como la disposición de las personas para actuar apropiadamente ante los desafíos en situaciones dadas, que no se reduce al uso de reglas y algoritmos, ni a enunciar conceptos y teoremas. Estas situaciones incluyen las escolares, pero también situaciones reales en las que se requiere que las personas activen las matemáticas para afrontar preguntas, resolver problemas y comprender fenómenos, relaciones y mecanismos para tomar una postura o decisión.
La naturaleza de estas competencias puede ser puramente intelectual, científica, profesional, financiera, moral o incluso práctica, y se precisa responder preguntas en o por medio de las matemáticas. Las acciones a las que hace referencia la definición no se limitan a cuestiones físicas; también pueden ser mentales. Incluso tomar la decisión de abstenerse de actuar en una situación dada es parte de esta disposición potencial de actuar. En este sentido, la competencia tiene un componente cognitivo, porque requiere la activación de diversas habilidades asociadas a conocimientos matemáticos como conceptos, algoritmos y fórmulas, entre otros. De esta forma, resulta imposible poseer una competencia matemática sin tener algún conocimiento matemático. Al mismo tiempo, es casi imposible tener conocimiento matemático sin tener un mínimo de competencia matemática.
Niss & Højgaard (2019) definen dos fases en esta disposición para la acción. Una es de carácter receptivo y se refiere a la capacidad potencial de la persona para relacionarse con planteamientos y procesos que ya le han presentado previamente en un contexto específico —por ejemplo, seguir y evaluar un planteamiento matemático—. La otra fase es de naturaleza constructiva, que se refiere a la capacidad del individuo para invocar y activar las competencias y usarlas con fines constructivos en situaciones específicas —por ejemplo, encontrar e implementar la resolución de un problema matemático, efectuar operaciones matemáticas o comunicar la construcción de un modelo matemático—.
Ante las condiciones de distanciamiento y confinamiento en el curso de la pandemia ocasionada por el covid-19, esta investigación se ocupa únicamente de la fase receptiva, que implica señalar las competencias necesarias para interpretar información relacionada con la pandemia, tales como: procesar datos cuantitativos, efectuar cálculos numéricos, hacer estimaciones razonables (Lüssenhop & Kaiser, 2020) e interpretar múltiples representaciones matemáticas, con el propósito de formular juicios fundados, participar de la reflexión colectiva y tomar decisiones consecuentes.
Las competencias matemáticas, ya sean en su fase receptiva o constructiva, están vinculadas al contexto de una situación o problema en el que la matemática tiene un rol importante. Para determinar o describir la forma en que las personas abordan la matemática, Niss & Højgaard (2019) señalan dos ámbitos de competencias matemáticas básicas. El primero está relacionado con la capacidad de plantear y responder preguntas, el cual tiene a su vez cuatro componentes: pensamiento matemático fundamental, plantear y resolver problemas matemáticos, tratar con modelos matemáticos y emprender razonamiento matemático. El segundo está relacionado con el dominio del lenguaje matemático, las construcciones y las herramientas. Este cuenta con cuatro componentes: tratar con representaciones matemáticas, tratar con símbolos y formalismo matemático, la comunicación matemática y, finalmente, las ayudas y herramientas matemáticas.
Como estas ocho competencias básicas están dirigidas a toda la actividad matemática general, fue necesario definir aquellas que se relacionan con los planteamientos matemáticos mostrados en las conferencias de prensa de la autoridad de salud mexicana. Para esto, se revisó el contenido de 59 conferencias con el propósito de identificar las competencias requeridas en su fase receptiva. Como resultado de esta revisión, se identificó el uso de tres tipos de competencia que establecen Niss & Højgaard (2019):
- competencia de modelado matemático: asociada con el análisis de modelos en contextos y situaciones extramatemáticas, en donde las matemáticas se utilizan para abordar preguntas en esos contextos, analizar sus propiedades y analizar y evaluar críticamente los modelos existentes o propuestos según los propósitos, datos, hechos y características que se modelan.
- competencia de representación matemática: relacionada con la capacidad de tratar con diferentes representaciones de entidades matemáticas, interpretar, traducir y transitar entre diferentes representaciones —por ejemplo, lo simbólico, lo tabular, lo gráfico, lo diagramático o lo visual—, tanto de los objetos matemáticos como de fenómenos, relaciones y procesos. Además, se relaciona con los alcances y las limitaciones de las representaciones involucradas en entornos determinados.
- competencia de dominio de símbolos y formalismo matemático: trata de la capacidad de relacionarse e interpretar símbolos matemáticos, expresiones simbólicas, transformaciones, sus reglas, la codificación y la decodificación de expresiones simbólicas.
Estas competencias no son dicotómicas en su posesión. De acuerdo con Niss & Højgaard (2019), se manifiestan de forma variada, por lo que no existe su posesión completa o exhaustiva. Para identificar el grado de posesión y/o progresión de una competencia, estos autores definen tres dimensiones de naturaleza cualitativa:
- cobertura: indica el grado de posesión de los aspectos y características de una competencia.
- radio de acción: indica la variedad de contextos y situaciones en los que se puede activar una competencia.
- nivel técnico: denota el grado de sofisticación de los conceptos matemáticos, resultados, teorías y métodos al ejercer la competencia.
Las conferencias de prensa que ofrece el gobierno mexicano en relación con la pandemia del covid-19 comenzaron a transmitirse todos los días a partir del 29 de febrero de 2020 y están disponibles en una página oficial. Para esta investigación, se analizaron 59 conferencias, desde el 29 de febrero hasta el 27 de abril. Sin embargo, eventualmente se consultaron otras de interés. El corte inicial fue definido por dos criterios. El primero fue la saturación de datos en los reportes, ya que el formato y contenido de la presentación se mantuvo muy similar con el paso de los días, pues cambiaba únicamente en la actualización de cifras y en puntualizaciones adicionales. La segunda cuestión, de carácter técnico, fue la decisión de hacer un corte para la elaboración de este artículo.
Para el análisis de los videos se definió escena como un intervalo de tiempo en el video donde el presentador aborda asuntos matemáticos, ya sea a partir de un apoyo visual en cualquiera de sus registros o en una intervención verbal independiente de cualquier apoyo visual. Para etiquetar los planteamientos matemáticos de las conferencias, ambos autores de la investigación trabajaron por separado e hicieron un registro independiente. Enseguida se discutieron las diferencias con el propósito de obtener una versión unificada. Para identificar las competencias de modelado, de representación y de símbolos matemáticos en su fase receptiva, se empleó la información del etiquetado de los planteamientos matemáticos y se definieron dos grados potenciales de posesión de la competencia: limitado y avanzado. Finalmente, para la competencia de cálculo, se identificaron las escenas donde el cálculo aritmético fuese la condición relevante para interpretar la información.
Resultados
De acuerdo con lo señalado por la Secretaría de Salud (Gobierno de México, 2020a), las conferencias de prensa tienen el propósito de exponer algunas consideraciones generales sobre las características del covid-19, reportar la situación de la pandemia tanto a nivel nacional como mundial en las últimas horas y comentar las medidas de prevención. La duración de cada conferencia es de aproximadamente una hora. Se mantuvo un esquema similar de presentación, esto es, un reporte de la evolución de la pandemia, la presentación y análisis de un tema asociado con el contexto de la pandemia y la sesión de preguntas y respuestas donde participan reporteros acreditados.
Los planteamientos matemáticos aparecen con más frecuencia en la primera parte de las conferencias, usualmente introducidas con diapositivas de apoyo. En menor medida, en la segunda parte se retoman algunas ideas matemáticas, lo cual es escaso en la tercera parte.
La primera tarea consistió en identificar las escenas —contextos específicos donde se hacen planteamientos matemáticos—. Por ejemplo, en la conferencia del 29 de febrero, el contexto es el riesgo de mortalidad respecto a grupos de edad. Los planteamientos matemáticos incluyen porcentaje, intervalo y decimales.
Ayer toqué el tema un poco de grupos de edad y riesgo de mortalidad, que yo creo que por ahí va su pregunta. En la serie más grande que se ha publicado básicamente de China, los mayores de 80 años tienen una probabilidad del 14.8 % de mortalidad; los mayores de 70 años tiene[n] una proporción de alrededor de 8 % de letalidad; los mayores de 60 años tienen 3.6 % de letalidad; los menores de 60 años, básicamente es menos del 2 %. (Gobierno de México, 2020a, 54:07)
Al tiempo que se definían las escenas, se catalogaron los planteamientos y las competencias matemáticas que aparecieron en las 59 conferencias. Después de la triangulación, se construyó una lista para agruparlos en tres ejes o áreas de conocimiento definidas a partir de la organización de los contenidos curriculares de la educación básica: tratamiento de la información, aritmética y funciones. La tabla 1 muestra la relación entre los temas matemáticos y el tipo de competencia que se les asocia. En términos generales, se observa que el modelado matemático y el cálculo matemático son las competencias más requeridas.
Tabla 1
Planteamientos matemáticos identificados asociados a competencias matemáticas
|
Área
|
Tema matemático
|
Modelado matemático
|
Representación matemática
|
Símbolos matemáticos
|
Cálculo matemático
|
|
Tratamiento de la información
|
Frecuencia acumulada
|
x
|
|
|
x
|
|
Intervalo
|
x
|
|
|
|
|
Media
|
x
|
|
|
x
|
|
Gráfica cartograma
|
x
|
x
|
|
x
|
|
Gráfica de barra
|
x
|
x
|
|
x
|
|
Gráfica poligonal
|
x
|
x
|
|
x
|
|
Gráficas estadísticas mixtas
|
x
|
x
|
|
x
|
|
Mediana
|
x
|
|
|
x
|
|
Gráfica circular
|
x
|
x
|
|
x
|
|
Tasa y densidad
|
x
|
|
|
x
|
|
Aritmética
|
Magnitudes y cantidades
|
x
|
|
x
|
x
|
|
Porcentajes
|
x
|
|
x
|
x
|
|
Proporción
|
x
|
|
|
x
|
|
Números negativos
|
x
|
|
x
|
x
|
|
Progresiones
|
x
|
|
|
x
|
|
Fracciones
|
x
|
|
|
x
|
|
Números decimales
|
x
|
|
|
x
|
|
Operaciones aritméticas
|
x
|
|
x
|
x
|
|
Cociente
|
x
|
|
|
x
|
|
Funciones
|
Comportamiento de curva
|
x
|
x
|
|
|
|
Rapidez de cambio
|
x
|
|
|
x
|
|
Predicción en curvas
|
x
|
x
|
|
|
|
Gráfica cartesiana
|
x
|
x
|
|
x
|
|
Patrones
|
x
|
|
|
|
|
Diferencial
|
x
|
|
|
x
|
|
Máximo
|
x
|
x
|
|
x
|
|
Incrementos y diferencias
|
x
|
|
|
x
|
Los datos que se presentan en las conferencias de prensa provienen de los reportes estadísticos del Sistema Nacional de Salud y corresponden a cada área de interés del programa de vigilancia epidemiológica. En la conferencia cada rubro es usualmente presentado a través de una gráfica o tabla. A partir de esta, se describe su estado actual, se hacen lecturas de su comportamiento y se estiman futuros escenarios. Así, todos los rubros en su conjunto integran una visión global del comportamiento de la pandemia, a partir de la cual también se hacen inferencias y se formulan escenarios a corto, mediano y largo plazo. En este sentido, una gráfica o una tabla es propiamente un modelo que describe el comportamiento de un evento, aunque también lo son en su conjunto. Por esta razón, la mayoría de los planteamientos matemáticos catalogados en la tabla anterior están vinculados con la competencia de modelación, que se refiere a la capacidad de las personas para relacionarse con los modelos propuestos, a fin de analizarlos críticamente a través de preguntas, interpretación de datos, hechos, características y propiedades del dominio matemático.
Dado que una parte importante de las conferencias consiste en describir la información contenida en gráficas y tablas, es necesario mencionar la relación que guarda con la competencia de representaciones matemáticas, la cual se refiere a la habilidad de las personas para relacionarse, interpretar y traducir diferentes representaciones de entidades matemáticas —por ejemplo: tabulares, gráficas y diagramáticas—.
Para el caso de los símbolos matemáticos, convenciones y formalismos, estos aparecen ocasionalmente en algunas diapositivas e intervenciones orales. Su importancia está asociada con la habilidad de las personas para interpretar símbolos y expresiones matemáticas, usados en operadores, símbolos para designar magnitudes y negativos.
Finalmente, la competencia de cálculo —organizada en dos niveles: el cálculo básico y computacional (habilidades numéricas primarias) y el cálculo analítico y estadístico (habilidades numéricas aplicadas e interpretativas)— está relacionado con la gran mayoría de los planteamientos matemáticos identificados, ya que implica la comprensión de datos, manipulaciones numéricas, conteo, comprensión de proporciones y porcentajes, comprensión de gráficos, análisis de información estadística y la toma de decisiones.
La siguiente etapa de la investigación consistió en identificar el grado de posesión individual para cada competencia. Al asumir que no son exhaustivas, se pueden presentar al menos dos escenarios: una condición limitada que implica un bajo nivel de reflexiones, contextos reducidos para la interpretación y un dominio básico de herramientas matemáticas; por otra parte, una condición avanzada, que implica involucrarse con los alcances de la competencia, reflexiones más profundas, interpretación y uso de múltiples contextos, así como un dominio sofisticado de conceptos y herramientas matemáticas. Estas dos definiciones son de carácter cualitativo y no deben entenderse como dicotómicas, sino que establecen un espectro de diferentes niveles de posesión intermedios. No obstante, para fines prácticos se ilustran a continuación estas dos condiciones para algunas de las competencias identificadas.
El nivel limitado de la competencia de modelado matemático en su dimensión de grado de cobertura se refiere a una escasa capacidad para interpretar modelos en contextos específicos, reconocer y obtener datos e identificar características. El nivel avanzado se relaciona con la capacidad para involucrarse con el modelo, reconocer su naturaleza, sus condiciones y sus características para estimar y explicar comportamientos. Se ilustra este nivel con la gráfica del modelo de proyección de casos confirmados de covid-19 en México de la figura 1, en la que se observa una gráfica de barras que corresponde al número de casos confirmados. En la misma superficie, se ven tres curvas de distribución que muestran tres posibles escenarios de ocurrencia con diferentes puntos máximos de casos confirmados y diferente duración del fenómeno. Para su interpretación se requiere identificar los datos, la relación de variables, estimar comportamientos gráficos y describir posibles escenarios.
En cuanto al radio de acción, el nivel limitado está asociado con la capacidad para interpretar un modelo en un contexto y reconocer escasamente sus características, así como una limitada capacidad para extraer información. El nivel avanzado implica el reconocimiento del modelo en una variedad de contextos y situaciones, la transferencia de información entre contextos y la capacidad para formular implicaciones del modelo en los contextos. Se ilustra este nivel con la gráfica del canal endémico de infecciones respiratorias (figura 2) en la que se observa su comportamiento en los últimos siete años ——verde, percentil 25 % (zona de éxito); amarillo, 25-50 % (zona de seguridad); y rojo, 50%-75% (zona de alarma)— con incidencia en semanas epidémicas. Este tipo de gráfico muestra un patrón de comportamiento habitual —histórico— sobre el cual se grafica la incidencia actual, en este caso la línea que corresponde al reporte del 2020. En los primeros meses del año se observa un comportamiento similar al histórico, pero que denota un incremento atípico de las enfermedades respiratorias para la semana 13. La interpretación del gráfico puede ayudar a detectar inicialmente cifras anormalmente altas o bajas de casos.
Figura 1
Covid-19 México: Proyección y observación de casos confirmados. Valle de México al 10 de mayo, 2020
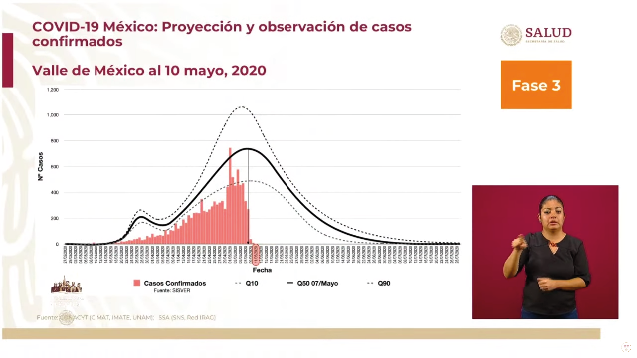
Nota. Captura de pantalla de Conferencia de Prensa #COVID19 de Gobierno de México, 2020g, mayo 11, YouTube. (https://youtu.be/h4pceSA8XbI)
Figura 2
México: canal endémico de infecciones respiratorias agudas a la SE Nº 13/2020
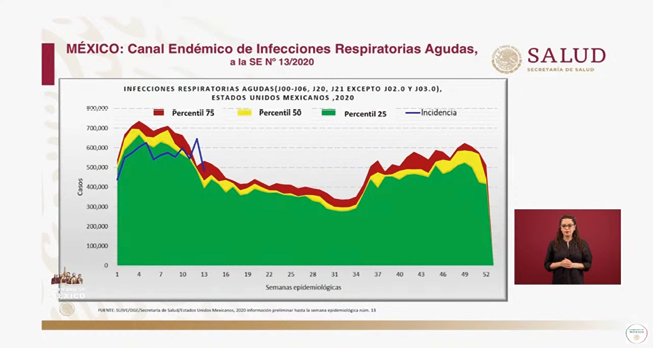
Nota. Captura de pantalla de #ConferenciaDePrensa: #Coronavirus #COVID19 #QuédateEnCasa de Gobierno de México, 2020c, abril 8, YouTube. (https://youtu.be/qPvXQ_MiZ4A)
El nivel técnico está asociado con la capacidad para reconocer, identificar e interpretar la matemática involucrada en el modelo. El avanzado exige dominio de símbolos matemáticos, decodificar e interpretar formalismos y transformaciones. Para ilustrar este nivel, se muestran dos gráficas del índice de movilidad para los estados mexicanos de Zacatecas e Hidalgo (figura 3). Su interpretación requiere tratar con un índice negativo expresado en porcentaje, identificar la variación por semana y describir e interpretar tendencias.
Figura 3
Covid-19 México: estados con menor respeto a la Jornada Nacional de Sana Distancia.
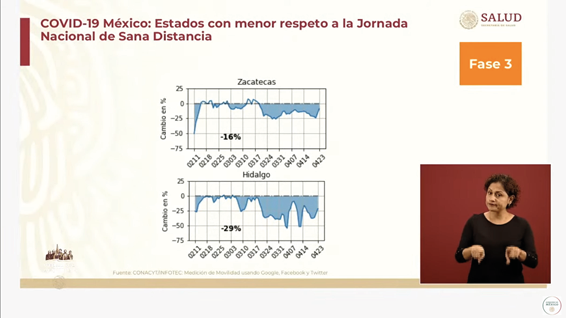
Nota. Captura de pantalla de Conferencia de Prensa: #Coronavirus #COVID19 de Gobierno de México, 2020f, abril 26, YouTube. (https://youtu.be/FoSzrgBJSfg)
En el caso de la competencia de representación, el grado de cobertura en el nivel limitado se refiere a la interpretación y comprensión básica de representaciones matemáticas. Exige un nivel básico de reflexión ante los planteamientos matemáticos: lectura de gráficas con un grado bajo de complejidad. El avanzado requiere una disponibilidad para analizar las representaciones, extraer información y explicar la naturaleza de la información, las variables y los comportamientos. Para ilustrar este nivel, se muestra una diapositiva con las defunciones confirmadas por covid-19 (figura 4) a través de una tabla y una gráfica. Aunque ambas representaciones comparten la misma información, el tránsito de una a otra requiere identificar las variables, entender la codificación y la frecuencia en barras e identificar la frecuencia acumulada.
El radio de acción en su nivel básico se refiere a la capacidad para interpretar información en un contexto. Exige una lectura básica para extraer información de las relaciones presentadas y una limitada capacidad para describir y explicar comportamientos. El avanzado requiere la capacidad para traducir diferentes representaciones de los datos, en diferentes contextos, con una amplia interpretación de los comportamientos de las gráficas y con la capacidad para formular conclusiones. Se ilustra este nivel con una gráfica que muestra diferentes comportamientos del índice de positividad de acuerdo con el tipo de enfermedad (figura 5). Se observa que la influenza mantiene un alto índice de positividad en las primeras semanas del año y decrece conforme se avanza a una temporada más cálida. Por el contrario, el índice de positividad del SARS CoV-2 tiene un notable aumento. Para su interpretación, es necesario reconocer el índice de positividad como un cociente entre las pruebas de laboratorio y resultados positivos y su expresión por medio de porcentajes. Las gráficas representan diferentes escenarios, aunque en conjunto permiten identificar el comportamiento atípico del covid-19.
Figura 4
Defunciones confirmadas por covid-19 por entidad federativa al 31/03/2020
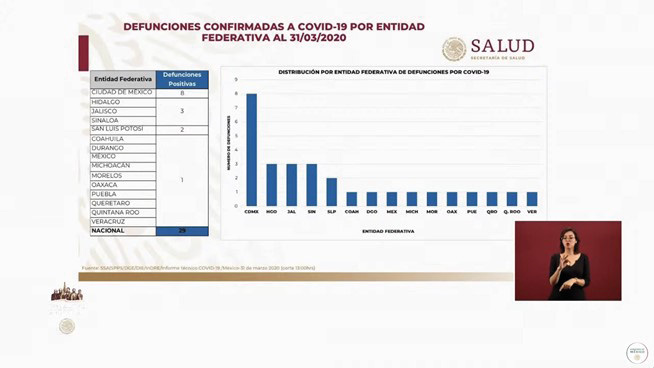
Nota. Captura de pantalla de #ConferenciaDePrensa: #Coronavirus #COVID19 de Gobierno de México, 2020b, marzo 31, YouTube. (https://youtu.be/wppaz_1mxN0)
Figura 5
Covid-19 México: índice de positividad por enfermedad viral, 20/04/2020
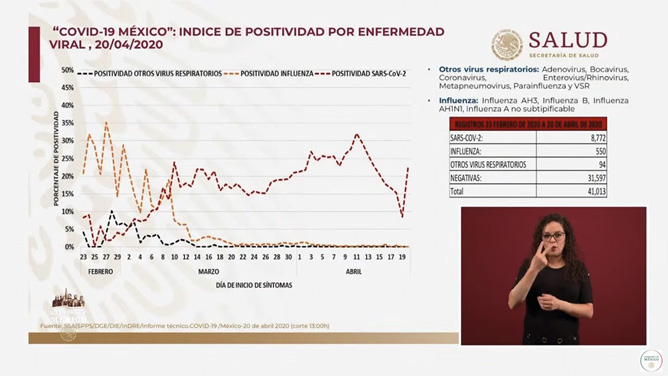
Nota. Captura de pantalla de Conferencia de Prensa: #Coronavirus #COVID19 de Gobierno de México, 2020e, abril 20, YouTube. (https://youtu.be/mo1kZCO1U-g)
El nivel técnico en su nivel avanzado implica la capacidad para reconocer, identificar e interpretar la matemática involucrada en una representación. Para ilustrar este nivel, se introduce la gráfica de muestras positivas a SARS-CoV 2 y el índice de positividad por semana (figura 6). Ambas gráficas comparten las semanas epidémicas, pero la gráfica de barras indica la cantidad de muestras en miles y la poligonal la positividad expresada en porcentaje. La positividad se expresa como un índice que determina el porcentaje de casos respecto al total de pruebas.
Figura 6
Covid-19 México: muestras positivas a SARS-CoV2 y positividad por semana epidemiológica
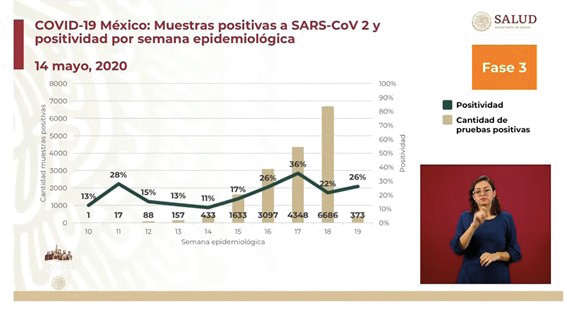
Nota. Captura de pantalla de Conferencia de Prensa #COVID19 de Gobierno de México, 2020h, mayo 15, YouTube. (https://youtu.be/xeyl-pDgfGU)
Respecto a la competencia de símbolos matemáticos y formalismo, se identificaron algunas escenas en las que aparecieron explícitamente símbolos matemáticos, en todos los casos integrados a sus contextos específicos. Los más recurrentes fueron el signo de negativo, el símbolo n para señalar el total de casos y los símbolos de operadores. Como su aparición fue marginal, no se ilustran casos particulares.
Sobre la competencia de cálculo, este apareció invariantemente implícito en todos las gráficas, tablas y reportes. Un aspecto relevante en esta competencia es la capacidad para dar sentido a la información, esto es, ofrecer un análisis crítico para la toma de decisiones. Un caso que ilustra esta competencia son los cálculos requeridos para seguir el modelo de estimación de casos positivos de covid-19 no observados (figura 7). Estos provienen de tres fuentes de datos:
- de las consultas clínicas de las 475 Unidades de Salud Monitoras de Enfermedades Respiratorias (USMER) distribuidas en todo el país —columnas 2, 3 y 4—.
- de las muestras procesadas de laboratorio en las USMER para diagnóstico de virus respiratorios de personas que cumplen la definición de caso sospechoso de covid-19 —columnas 5, 6 y 7—.
- de los datos de la vigilancia epidemiológica a través de consultas médicas en las 26 000 unidades de salud en todo el país —columna 8—.
La interpretación de la tabla requiere un nivel avanzado de habilidades de cálculo, particularmente de proporciones, porcentajes y tasas. Una aproximación a la información de la tabla es la siguiente. En la columna 2 se reportan todos los casos de enfermedades respiratorias de las 374 unidades monitoras. La columna 3 es un subgrupo con los casos que presentan signos y síntomas de influenza —que son similares a los de covid-19—. Es decir, en esta columna están presentes casos de influenza y covid-19. La columna 4 muestra el porcentaje de estos casos de influenza respecto de todas las enfermedades respiratorias de la columna 2. A partir de la información de la columna 3, tiene sentido la pregunta: ¿cuántos casos presentan covid-19? Una forma de determinarlo es a través de la prueba de laboratorio que se reporta en la columna 7. Particularmente, en la semana 10 se observa que se hicieron 991 pruebas que confirmaron 27 casos de covid-19. Esto significa que el índice de positividad fue de 2.72 %. Este índice se podría aplicar al subgrupo con signos y síntomas de influenza (columna 3), lo que produciría un estimado de 67 casos. Sin embargo, hay que considerar que el reporte de las unidades monitoras (columna 2) es tan solo un subgrupo de reporte de vigilancia epidemiológica nacional (columna 8), por lo que, para no duplicar datos, se debe restar el reporte nacional del de las unidades monitoras. A partir de este resultado, es posible aplicar el porcentaje que determina la proporción de los pacientes con signos y síntomas de influenza (columna 4) y así determinar un estimado nacional con esta condición de salud (columna 9). Finalmente, a partir de estos datos, se puede aplicar el índice de positividad para determinar el estimado nacional de covid-19 (columna 10). Hay que considerar que estos datos se necesitan estandarizar por grupos de edad y por diversidad geográfica, por lo que las cifras presentan una desviación.
Este modelo de estimación de casos permite formular diversas conclusiones. Por ejemplo, la proporción entre casos positivos y número de casos estimados, el incremento de casos por semana, la importancia de más pruebas de laboratorio, el comportamiento en el índice de positividad y la enorme cantidad de estimados positivos comparada con los resultados de laboratorio.
Figura 7
México, covid-19: estimación de casos
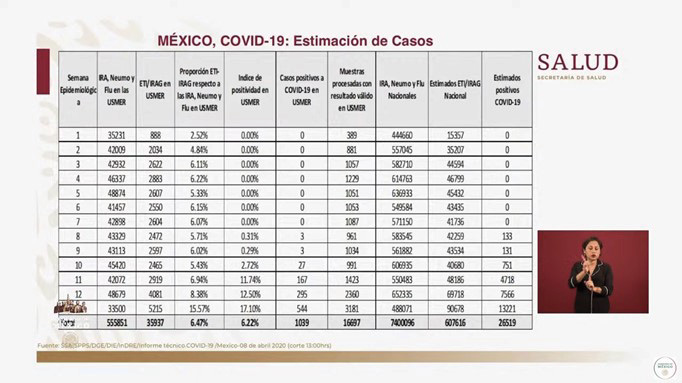
Nota. Captura de pantalla de #ConferenciaDePrensa: #Coronavirus #COVID19 #QuédateEnCasa de Gobierno de México, 2020c, abril 8, YouTube. (https://youtu.be/qPvXQ_MiZ4A)
Discusión y conclusiones
La crisis sanitaria provocada por la pandemia del covid-19 ha demostrado lo vulnerables que somos los humanos. Esta condición de vulnerabilidad se acentúa en personas con comorbilidades —como la hipertensión, diabetes y obesidad—, ya que tienen más riesgo de complicaciones cuando padecen covid-19 (Gobierno de México, 2020d). Este referente no es nada alentador cuando la Encuesta Nacional de Salud en México (INEGI, 2018b) reporta que a nivel nacional el porcentaje de adultos de 20 años y más con sobrepeso y obesidad es de 75.2 %. Este escenario parece indicar que más de tres cuartas partes de la población mexicana está en el grupo de alta vulnerabilidad como consecuencia de los malos hábitos de alimentación, de las ineficientes políticas de salud y de estilos de vida poco saludables.
Este artículo postula otra variable a esta condición de vulnerabilidad. Para seguir con la discusión de Heilmann (2020), existe una correlación entre el dominio de las habilidades de cálculo y la condición de salud, ya que un bajo nivel de habilidades aritméticas conduce a serias dificultades para comprender los riesgos de la salud de determinados hábitos y comportamientos. De acuerdo con el PIAAC (OCDE, 2019) el 40 % de los adultos en ocupación laboral están ubicados por debajo del nivel 1, donde se pide apenas contar, clasificar, realizar operaciones aritméticas básicas con números enteros o dinero y reconocer representaciones. Estas limitaciones conducen a serias dificultades para manejar diversas situaciones y tareas de la vida diaria, así como para interpretar e incidir en la realidad social.
En particular, este artículo sostiene que un bajo dominio de la aritmética compromete la salud ante la incapacidad de acceder a la información, procesar, interpretar, comunicarse y actuar a partir de datos numéricos, cuantitativos, gráficos y de probabilidad. Según este argumento, el propósito de esta investigación fue identificar las competencias matemáticas que requieren los ciudadanos para interpretar los planteamientos matemáticos en los modelos que describen la evolución de la pandemia del covid-19, particularmente los que ofrece la autoridad sanitaria del Gobierno Federal de México.
Al respecto, se ofrecen dos consideraciones: en primer lugar, un modelo matemático es una interpretación de lo que realmente ocurre. Es decir, es una simplificación con un número limitado de variables que tiene el alcance de describir posibles escenarios bajo condiciones específicas. No obstante, no deja de existir una brecha entre lo que señala el modelo y lo que ocurre en la realidad.
En este escenario se identifican dos actores: por una parte, la autoridad sanitaria, que tiene la responsabilidad de elegir el modelo más conveniente para el contexto; por otra parte, una ciudadanía participativa, con habilidades matemáticas para acceder e interpretar la información de los modelos y actuar en consecuencia. Las reflexiones sobre el primer actor rebasan las pretensiones de este artículo. Sin embargo, en el contexto de la pandemia del covid-19, cualquier decisión de la autoridad sanitaria tiene un costo de vidas humanas. Retrasar o adelantar el confinamiento implica un cálculo matemático de vidas humanas frente al costo económico de paralizar el país. ¿Realmente hay que escatimar gastos o la prioridad es salvar vidas?
El artículo se ocupó de reflexionar sobre el segundo actor, particularmente sobre la interacción entre el ciudadano y los planteamientos matemáticos. En este contexto está la segunda consideración: la capacidad de acceder e interpretar la matemática involucrada en un modelo posibilita una lectura de fenómeno. Es decir, permite construir una racionalidad sobre la pandemia, pero también sobre el modelo mismo. El problema es que con el bajo nivel de habilidades de cálculo y con limitadas competencias de modelado, de interpretación de representaciones y de símbolos matemáticos, tal como lo reporta el PIAAC (ODCE, 2019), la población tiene serias limitaciones para argumentar, analizar, desarrollar una postura crítica sobre los modelos y actuar responsablemente ante la pandemia.
La revisión que ofrece este artículo muestra que, ante los planteamientos matemáticos, las personas necesitan un dominio de competencias en amplio espectro, desde básicas hasta avanzadas. Particularmente, la competencia de modelación y la de cálculo son las más demandadas, debido a que cada gráfica o reporte es en sí un modelo. Por otra parte, la necesidad de efectuar cálculos para interactuar con los reportes está presente en todos los planteamientos matemáticos.
La discusión de este artículo apunta en varias direcciones:
- la tarea pendiente del sistema educativo para proveer un dominio de la matemática más allá de las habilidades procedimentales y para fortalecer habilidades numéricas aplicadas e interpretativas asociadas con la toma de decisiones y el desarrollo de argumentos críticos.
- la importancia del pensamiento matemático para actuar en el mundo con un compromiso crítico.
- la alta vulnerabilidad de las personas derivada de la precariedad matemática que impide hábitos saludables y preservar la salud, entre muchos otros.
Referencias
Coben, D., & O’Donoghue, J. (2020). Adults Learning Mathematics. En S. Lerman (Ed.), Encyclopedia of Mathematics Education (pp. 24-31). Springer International Publishing. https://doi.org/10.1007/978-3-030-15789-0_5
Cutler, D., & Lleras-Muney, A. (2010). Understanding Differences in Health Behaviors by Education. Journal of Health Economics, 29(1), 1-28. https://doi.org/10.1016/j.jhealeco.2009.10.003
Furman, M. (2012). ¿Qué ciencia estamos enseñando en escuelas de contextos de pobreza? Praxis & Saber, ٣(5), 15-52. https://doi.org/10.19053/22160159.1138
Gal, I., Grotlüschen, A., Tout, D., & Kaiser, G. (2020). Numeracy, adult education, and vulnerable adults: a critical view of a neglected field. ZDM - Mathematics Education, 52(3), 377-394. https://doi.org/10.1007/s11858-020-01155-9
Geiger, V., Goos, M., & Forgasz, H. (2015). A rich interpretation of numeracy for the 21st century: a survey of the state of the field. ZDM - International Journal on Mathematics Education, 47(4), 531-548. https://doi.org/10.1007/s11858-015-0708-1
Gobierno de México. (2020a, febrero 29). #ConferenciaDePrensa: Coronavirus #COVID19 [Video]. YouTube. https://youtu.be/9N0Ti0XCiUs
Gobierno de México. (2020b, marzo 31). #ConferenciaDePrensa: #Coronavirus #COVID19 [Video]. YouTube. https://youtu.be/wppaz_1mxN0
Gobierno de México. (2020c, abril 8). #ConferenciaDePrensa: #Coronavirus #COVID19 #QuédateEnCasa [Video]. YouTube. https://youtu.be/qPvXQ_MiZ4A
Gobierno de México. (2020d, abril 19). Conferencia de Prensa #Coronavirus #COVID19 [Video]. YouTube. https://youtu.be/XmCh3tRKSTY
Gobierno de México. (2020e, abril 20). Conferencia de Prensa: #Coronavirus #COVID19 [Video]. YouTube. https://youtu.be/mo1kZCO1U-g
Gobierno de México. (2020f, abril 26). Conferencia de Prensa: #Coronavirus #COVID19 [Video]. YouTube. https://youtu.be/FoSzrgBJSfg
Gobierno de México. (2020g, mayo 11). Conferencia de Prensa #COVID19 [Video]. YouTube. https://youtu.be/h4pceSA8XbI
Gobierno de México. (2020h, mayo 15). Conferencia de Prensa #COVID19 [Video]. YouTube. https://youtu.be/xeyl-pDgfGU
Golbeck, A., Ahlers-Schmidt, C., Paschal, A., & Dismuke, S. (2005). A definition and operational framework for health numeracy. American Journal of Preventive Medicine, 29(4), 375-376. https://doi.org/10.1016/j.amepre.2005.06.012
Heilmann, L. (2020). Health and numeracy: the role of numeracy skills in health satisfaction and health-related behaviour. ZDM - Mathematics Education, 52(3), 407-418. https://doi.org/10.1007/s11858-019-01106-z
Instituto Nacional de Estadística y Geografía. (2018a). Estadísticas a propósito del Día Mundial de la Población (11 de julio), Datos Nacionales. Comunicación Social. INEGI.
Instituto Nacional de Estadística y Geografía. (2018b). Encuesta Nacional de Salud. Comunicación Social. INEGI.
Jablonka, E. (2020). Critical Thinking in Mathematics Education. En S. Lerman (Ed.), Encyclopedia of Mathematics Education (pp. 121-125). Springer Netherlands. https://doi.org/10.1007/978-94-007-4978-8_35
Lampert, T., & Kroll, L. (2010). GBE kompakt: Armut und Gesundheit. GBE Kompakt, 5, 10. https://bit.ly/3jwkDAJ
Lüssenhop, M., & Kaiser, G. (2020). Refugees and numeracy: what can we learn from international large-scale assessments, especially from TIMSS? ZDM - Mathematics Education, 52(3), 541-555. https://doi.org/10.1007/s11858-019-01111-2
Montecino, A., & Valero, P. (2016). The disorder of mathematics education: Challenging the sociopolitical dimensions of research. En H. Straehler-Pohl, A. Pais, & N. Bohlmann (Eds.), The Disorder of Mathematics Education: Challenging the Sociopolitical Dimensions of Research (pp. 135-152). Springer. https://doi.org/10.1007/978-3-319-34006-7
Niss, M., & Højgaard, T. (2019). Mathematical competencies revisited. Educational Studies in Mathematics, 102(1), 9-28. https://doi.org/10.1007/s10649-019-09903-9
Niss, M., & Jablonka, E. (2020). Mathematical Literacy. En S. Lerman (Ed.), Encyclopedia of Mathematics Education (pp. 391-396). Springer Netherlands. https://doi.org/10.1007/978-94-007-4978-8_100
O’Donoghe, J. (2002). Numeracy and Mathematics – Information Sheet. Irish Mathematical Society Bulletin, 48, 47-55.
Organización para la Cooperación y el Desarrollo Económicos. (2012). Literacy, numeracy and problem solving in technology-rich environments – framework for the OECD survey of adult skills. OCDE.
Organización para la Cooperación y el Desarrollo Económicos. (2014). Education at a glance 2014: OECD indicators. OCDE.
Organización para la Cooperación y el Desarrollo Económicos. (2019). Skills matter: Additional results from the survey of adult skills. OECD.
Unesco. (2007). Educación para todos en 2015 ¿Alcanzaremos la meta? Unesco.