Cartographies of Research with Children in Mathematics Education: a Review of Works Published in Brazil

Abstract

In order to map the ways in which children appear as objects in Mathematics Education research, we reviewed papers published since 2012 in four journals and in proceedings of two of the most important events in the area in Brazil. We selected papers that dealt with childhood or that conducted research with children. Our selection resulted in 60 papers, 46 of which were published in journals and 14 in proceedings of events. We discussed the following points: when conducting research with children, Mathematics Education has not explicitly problematized concepts of childhood and children that guide its reflections; the papers operate with an equivalence between the notions of child and student; Piagetian-inspired cognitivism is the hegemonic regime for reading children´s mathematical activity; the research has promoted an anticipation of the use of didactic-methodological tools of Mathematics Education for increasingly younger children, with emphasis on papers that use Statistical Education and Mathematical Modelling in Early Childhood Education. The article points to the need to reconsider the problem of childhood in Mathematics Education in order to emphasize creative processes that escape the hegemonic regimes of producing children´s subjectivities.

Keywords: mathematics education, childhood, cartography

Cartografías de Investigaciones con Niños en Educación Matemática: una Revisión de Trabajos Publicados en Brasil

Resumen

Con el objetivo de mapear las formas en que los niños aparecen como objetos en la investigación en Educación Matemática, revisamos trabajos publicados a partir de 2012 en cuatro revistas y en los anales de dos de los eventos más importantes del área en Brasil. Se seleccionaron trabajos que versaban sobre la infancia o que realizaban investigaciones con niños. Nuestra selección resultó en 60 trabajos, 46 de los cuales fueron publicados en revistas y 14 en anales de eventos. Se discuten los siguientes puntos: al realizar investigaciones con niños, la Educación Matemática no ha problematizado explícitamente las concepciones de infancia y de infancia que orientan sus reflexiones; las obras operan con una equivalencia entre las nociones de niño y estudiante; El cognitivismo de inspiración piagetiana es el régimen hegemónico de lectura de la actividad matemática de los niños; Las investigaciones vienen promoviendo una anticipación del uso de herramientas didáctico-metodológicas en la Educación Matemática para niños cada vez más pequeños, con énfasis en trabajos que utilizan la Educación Estadística y la Modelación Matemática en la Educación Infantil. El artículo apunta a la necesidad de sustituir el problema de la infancia en la Educación Matemática para dar énfasis a procesos creativos que escapan a los regímenes hegemónicos de producción de subjetividades infantiles.

Palabras clave: educación matemática, infancia, cartografía

Introdução

Este artigo é parte de um projeto de pesquisa maior intitulado Crianças e matemáticas em produção na (pré)escola: cartografias de uma infância da (Educação) Matemática. Esse projeto, apoiado com bolsas de Iniciação Científica de programa institucional próprio da Universidade Federal de Juiz de Fora, tem como questão mais geral a investigação dos modos pelos quais as crianças se produzem ao produzirem matemática. Essa questão deriva da pesquisa de doutorado de Cammarota (2021), que investiga como a Educação (Matemática) produz discursos sobre a infância.

Em seu conjunto, a pesquisa busca cartografar os processos de subjetivação e dessubjetivação das crianças da Educação Infantil e dos primeiros dois anos do Ensino Fundamental à medida que se envolvem na produção de conhecimento matemático, ou seja, busca compreender como as crianças produzem a si mesmas e como se relacionam com o mundo ao seu redor por meio da matemática e de sua produção. A pesquisa tem, por isso, uma natureza política que envolve, por um lado, questões das relações de poder e dos sistemas semióticos dominantes na Educação e na Matemática, ao mesmo tempo em que se indaga sobre como as crianças são produzidas por esses sistemas.

(...) é próprio da criança fazer funcionar suas máquinas desejantes na máquina social técnica. Nesse sentido, é o próprio desejo como produção que cria no interior das máquinas sociais, no interior do campo social. Seria preciso se perguntar como a produção infantil pode fazer operar suas máquinas desejantes na máquina social técnica. Mais ainda, no âmbito dessa pesquisa, seria preciso perguntar como a matemática pode atuar como uma máquina que se acopla à infância, produzindo cortes no fluxo do desejo, colocando-o a serviço de uma certa configuração do campo social. (Cammarota, 2021, p. J-8)

Por outro lado, a pesquisa busca problematizar a nomeação do que as crianças fazem em termos de matemática como parte de um problema político. Em outras palavras, seria preciso pensar em como nós, adultos, pesquisadores, nomeamos aquilo que as crianças fazem de matemática. Isso sugere a necessidade de problematizar1 discursos instituídos na Educação (Matemática) e em seus modos de compreender as crianças e de compreender os modos pelos quais as crianças se relacionam com a matemática na escola.

É no sentido de procurar cartografar os modos pelos quais crianças e infância têm sido tratadas em pesquisas da Educação Matemática que este artigo surge. Conduziu-se uma cartografia abrangendo pesquisas publicadas no Brasil com o objetivo de mapear parte dos estudos divulgados em veículos científicos conceituados na área de Educação Matemática. Procuramos pensar aqui as seguintes questões: que educação matemática vem se configurando na relação com as crianças e com a infância? Como a educação matemática vem fazendo pesquisa com crianças?

Neste artigo, procuramos destacar quatro pontos de interesse que derivam de planos comuns produzidos a partir desse mapeamento e divulgar os primeiros resultados da pesquisa maior.

Optamos por trabalhar com a revisão de artigos publicados nos periódicos Bolema, da Universidade Estadual Paulista “Júlio de Mesquita Filho” – campus Rio Claro, Zetetiké, da Universidade Estadual de Campinas e Boletim GEPEM, da Universidade Federal Rural do Rio de Janeiro em função do extenso histórico de destaque desses periódicos na Educação Matemática brasileira. Trabalhamos também com o periódico Perspectivas da Educação Matemática, da Universidade Federal do Mato Grosso do Sul, cuja produção vem se destacando na última década na área. A maior parte dos artigos selecionados é relativa à produção científica brasileira, mas também verificamos que há trabalhos de pesquisa conduzidos em outros países, destacadamente Portugal e países hispano falantes da América Latina.

A revisão de trabalhos também se deu em anais de dois grandes eventos da área e que são organizados pela Sociedade Brasileira de Educação Matemática (SBEM): o Simpósio Internacional de Pesquisa em Educação Matemática (SIPEM) e o Encontro Nacional de Educação Matemática (ENEM). No interior desses eventos, funciona um Grupo de Trabalho - GT 01 - Matemática na educação infantil e nos anos iniciais do Ensino Fundamental. Os principais objetivos do GT, listados no site da Sociedade Brasileira de Educação Matemática (SBEM), são a formação docente, aprendizagem e o conhecimento matemático dos estudantes dos primeiros anos da escolarização e na Educação Infantil e a produção de recursos didáticos para esses anos.

Sendo assim, dado o escopo do interesse dessa pesquisa, revisamos trabalhos publicados em anais do ENEM e do SIPEM que se encontravam abrigados no GT012.

Infâncias e crianças: entre a história, a política e a educação

A noção de infância é profundamente enraizada na cultura e na linguagem. Sua etimologia, originada do latim infantia, revela uma perspectiva intrigante: infans refere-se ao indivíduo que ainda não é capaz de falar, aquele que não possui voz. Esta raiz etimológica lança luz sobre como, ao longo da história, a infância foi percebida como um período de vida em que as crianças não tinham voz ativa na sociedade, sendo frequentemente relegadas à margem do discurso adulto.

A concepção de infância ao longo da história é um tema complexo que variou significativamente ao longo dos séculos. Ao analisarmos o passado, podemos identificar padrões e contrastes na forma como as sociedades percebiam as crianças. A compreensão histórica da infância é essencial para entender como as crianças foram vistas ao longo do tempo. Ariès (1981) destaca que a concepção da infância foi historicamente construída a partir da modernidade. Ele argumentou que até então as crianças não eram vistas como sujeitos de direitos ou como seres em desenvolvimento, mas como miniaturas dos adultos. Essa perspectiva dominante na sociedade moldou a maneira como as crianças eram tratadas e compreendidas.

De certa maneira, pode-se dizer que Ariès afirma a ausência de uma concepção sociológica de infância até a modernidade, uma vez que as experiências, necessidades e perspectivas das crianças não eram consideradas socialmente relevantes ou distintas das dos adultos. Uma concepção sociológica de infância envolve a compreensão das crianças como um grupo social com características, papéis e relações específicas na sociedade, reconhecendo que essas características e relações são moldadas por fatores sociais, culturais e históricos. A ausência dessa perspectiva sociológica sobre a infância reflete na invisibilização das dinâmicas sociais que envolvem as crianças e suas interações com a sociedade em que vivem.

No entanto, Kohan (2003) nos coloca a refletir sobre a presença de uma concepção política de infância, mesmo em épocas nas quais não se pensava na infância mediante um prisma sociológico. Platão abordou a importância da educação na formação das crianças como parte fundamental de sua filosofia. Ele acreditava que a educação adequada poderia moldar jovens para se tornarem governantes virtuosos, buscando solucionar problemas culturais e políticos na pólis. A natureza da infância e sua importância na formação dos indivíduos eram temas centrais nas ideias de Platão, argumentando que as crianças eram seres potencialmente moldáveis e maleáveis, capazes de serem influenciados e educados para se tornarem cidadãos virtuosos.

Nessa conjuntura, a infância era considerada uma fase inferior à idade adulta, tanto em termos físicos quanto espirituais. Platão enfatizava a necessidade de uma educação cuidadosa desde os primeiros momentos da vida, alegando que as crianças eram como tábuas em branco que podiam ser moldadas para o bem da cidade. O filósofo também enfatizava a importância de escolher cuidadosamente os relatos e histórias que as crianças ouviam, a fim de inculcar nelas os valores desejados. Associava-se à infância a falta de experiência e a inadequação social. O sistema educacional visava orientar as crianças para se tornarem filósofos-governantes e a educação era vista como um processo normativo, no qual os adultos moldavam os jovens de acordo com um modelo predefinido de pólis justa.

Em essência, a criança era vista como uma promessa de futuro, um instrumento para a construção da pólis desejada e deveria ser moldada para alcançar esse objetivo. Não existia, portanto, uma concepção sociológica de infância, mas uma concepção política arraigada na filosofia de Platão.

Apesar das mudanças ocorridas ao longo dos séculos, é interessante notar como concepções antigas de infância lançaram as bases para ideias persistentes que ecoam na contemporaneidade. Isso inclui a visão da infância como um estado de inferioridade, o que justifica a autoridade adulta e a capacidade de governança sobre as crianças, sustentando a premissa de que a criança é governável apenas devido à sua condição de inferioridade perante os adultos.

Ademais, bem como diz Kohan (2003), os adultos impunham às crianças as expectativas de uma pólis justa e as moldavam de acordo com essa visão. A continuidade dessa dinâmica ao longo do tempo se configura na medida em que as crianças continuam a ser percebidas como agentes de construção do futuro, carregando as expectativas e as aspirações de suas sociedades. O que vai ao encontro a ideia da criança preenchida apresentada em Deligny (2015), que faz referência a como os adultos exercem uma influência significativa sobre as crianças ao preenchê-las com suas expectativas e moldá-las de acordo com suas próprias concepções e aspirações, transformando-as em promessas de futuro. Nesse sentido, a criança se torna um vir-a-ser do adulto que será posteriormente promovida ao título de pessoa por inteiro.

(...) constata-se que nestas últimas a Iniciação, a entrada da criança nos papéis especificados pelo campo social adulto, situa-se aproximadamente em torno de 9-12 anos. Até aí, ela não precisa respeitar rigorosamente as proibições do grupo. Só quando ela é promovida ao título de “pessoa por inteiro”, de membro do clã, é que ela deve se dobrar às normas do grupo, o que faz com que ela se beneficie, em contrapartida, do prestígio e das vantagens materiais próprias de cada etapa desta promoção. (Guattari, 1977, p. 50).

Isso resulta na exclusão da infância, projetando uma imagem de desvalor das crianças e rejeição do contato com a alteridade. No entanto, visões contemporâneas, como a de Giorgio Agamben, Guattari e Deligny desafiam essa perspectiva tradicional. Agamben argumenta que a infância não é apenas uma fase, mas uma condição da experiência humana. Ele destaca que a aprendizagem da linguagem, uma característica fundamental da humanidade, permanece ligada à infância e à exterioridade, enfatizando a importância da infância como parte integral da existência humana (Agamben, 2001).

O poeta Manoel de Barros3 (2010) compartilha a visão de que a criança e o poeta partilham semelhanças. Ambos empregam a linguagem como uma ferramenta para expandir os horizontes do mundo, tanto o vivido quanto o imaginado. A infância é um período repleto de inquietação, uma fase de reconstrução do universo e de atribuição de significados. As brincadeiras se destacam como o espaço no qual a criança exerce sua imaginação, criação e desenvolvimento, e, em seus poemas, Barros reflete sobre essa capacidade intrínseca da criança de se relacionar com o mundo, de inventar seus próprios jogos e de atribuir significados sem depender da intervenção de adultos.

Tomando como inspiração a poesia de Manoel de Barros sobre criança, a concepção de infância por meio da qual constitui-se este texto e que conduziu a cartografia realizada é intrinsecamente ligada à criação e à invenção, mas também possui uma dimensão política. Nessa concepção criança não é uma miniatura do adulto em formação, mas um agente ativo e cri(ativo) que contribui significativamente para a construção do conhecimento e do mundo que a cerca. A infância não é um estado fixo que a criança atinge em uma idade específica e depois é promovida à condição de adulto, mas um processo em constante transformação, um processo de tornar-se, de experimentação e reinvenção.

Nesse sentido, nos inspiramos na filosofia de Deleuze e Guattari (1997), particularmente em seu conceito de devir-criança, que implica romper com as limitações impostas pelo tempo cronológico e reconhecer que a infância é uma condição que persiste no adulto como uma virtualidade que se manifesta enquanto capacidade contínua de divergência e diferenciação da cognição, abrindo caminho para a exploração da dimensão inventiva da cognição e, portanto, do conhecimento.

A perspectiva do devir-criança não trata de tornar-se uma criança empírica ou de infantilizar-se, mas sim de reconhecer que a infância é uma dimensão sempre contemporânea: ela implica em um encontro entre o adulto e a criança, em que ambos se diferenciam mutuamente e produzem algo novo e singular. Esse encontro não está restrito aos primeiros anos de vida, mas persiste ao longo da existência. Essa concepção não apenas redefine a infância, mas também possui implicações políticas importantes, nos colocando a repensar a relação entre adultos e crianças, destacando a necessidade de ouvir e valorizar as vozes das crianças em nossa sociedade.

Neste contexto, a criança é um sujeito de direito, capaz de contribuir para o discurso social. Não mais encaradas como adultos em miniatura, nem como um vir-a-ser do adulto, mas como um modo de vida cujas perspectivas são singulares. A infância representa um período crucial de desenvolvimento, onde as crianças têm pressa de viver e buscam experiências significativas que não podem ser adiadas para o futuro. Inspirados pelo escritor mineiro Carlos Drummond de Andrade, citamos: “Criança tem pressa de viver e não lhe prometem uma compensação no futuro, a necessidade é urgente, o bálsamo que venha já, amanhã será tarde demais…” (2008, p. 3). É esse, pois o sentido, de produzir uma revisão de trabalhos que tratam da infância: compreender os processos por meio dos quais a pesquisa em Educação Matemática produz promessas e compensações no futuro para as crianças ao mesmo tempo em que ouve delas a pressa de viver, a necessidade urgente de inventar e produzir novos mundos.

O dispositivo revisão: que cartografia?

No primeiro ano de pesquisa, nossos interesses se voltaram mais particularmente para a revisão de trabalhos publicados em anais de eventos e periódicos qualificados no campo da Educação Matemática. Seguimos pelo caminho apontado em Cammarota (2021): a cartografia pode ser pensada não só como um método de pesquisa, mas também como um modo de habitar o mundo e como um conceito filosófico, como um princípio aproximativo do rizoma discutido em Deleuze e Guattari (2011b).

Rolnik (2016) nos lembra que a prática da cartografia, em uma dimensão micropolítica, “[...] tem a ver com o poder em sua dimensão de técnicas de subjetivação – estratégias de produção de subjetividade –, dimensão fundamental da produção e reprodução do regime em curso” (Rolnik, 2016, p. 70). Assim sendo, ao nos ocuparmos com a revisão de trabalhos que tratam da infância, apontamos para uma cartografia dos modos mais dominantes de pensar e lidar com crianças fazendo matemática que vem se configurando na pesquisa no campo da Educação Matemática; ao mesmo tempo, marcamos possibilidades de mapear linhas de fuga que traçam dissensos no interior dos modos dominantes de pesquisar em Educação Matemática. Neste artigo, apresentamos mais especialmente a primeira dessas tarefas, com mapeamentos de pontos de interesse que emergiram do processo de seleção e estudo dos trabalhos. Esses pontos, como veremos a seguir, constituem planos comuns aos trabalhos.

Como, então, cartografar os trabalhos em Educação Matemática? Seguimos a pista de Kastrup e Barros (2009), que dizem que a cartografia requer dispositivos para fazer funcionar a pesquisa. Foucault (2017) discute a noção de dispositivo como um conjunto de elementos heterogêneos, o dito e o não dito, cuja função é, dentre outras, a de uma certa manipulação das relações de forças.

o dispositivo alia-se aos processos de criação e o trabalho do pesquisador, do cartógrafo, se dá no desembaraçamento das linhas que o compõem - linhas de visibilidade, de enunciação, de força, de subjetivação. Trabalhar com dispositivos implica-nos, portanto, com um processo de acompanhamento de seus efeitos, não bastando apenas pô-los a funcionar. (Kastrup & Barros, 2009, p. 79)

É nesse sentido que utilizamos como um dispositivo dessa pesquisa a revisão sistemática de literatura, conforme discutida em Galvão (٢٠١٩). É por meio desse modo de proceder que poderemos desembaraçar linhas de visibilidade, enunciação, força, subjetivação e dessubjetivação que a pesquisa em Educação Matemática vem produzindo com crianças.

Galvão (2019) nos apresenta a revisão sistemática como uma técnica utilizada para identificar, avaliar e interpretar estudos relevantes relacionados a uma questão de pesquisa específica ou a um fenômeno de interesse.

É uma modalidade de pesquisa, que segue protocolos específicos, e que busca entender e dar alguma logicidade a um grande corpus documental, especialmente, verificando o que funciona e o que não funciona num dado contexto. Está focada no seu caráter de reprodutibilidade por outros pesquisadores, apresentando de forma explícita as bases de dados bibliográficos que foram consultadas, as estratégias de busca empregadas em cada base, o processo de seleção dos artigos científicos, os critérios de inclusão e exclusão dos artigos e o processo de análise de cada artigo. Explicita ainda as limitações de cada artigo analisado, bem como as limitações da própria revisão. (Galvão, 2019, pp. 58-59)

Então, ao nos perguntarmos que cartografia se constitui atravessada pelo dispositivo revisão, deslocamos a ideia da produção de categorias gerais que aglutinam os trabalhos revisados para uma ideia da constituição de planos comuns entre os textos. Kastrup e Passos (2013, p. 265) discutem a cartografia como o traçado de planos comuns argumentando que:

Tal plano é dito comum não por ser homogêneo ou por reunir atores que manteriam entre si relações de identidade, mas porque opera comunicação entre singularidades heterogêneas, num plano que é pré-individual e coletivo. Trata-se de incluir as múltiplas linhas ou vetores [...] para que possamos fazer emergir o entendimento de uma realidade complexa. Em tal rede estamos todos incluídos [...]: diferentes sujeitos, objetos e instituições, cabendo, portanto, às estratégias de pesquisa acessar o plano que articula, conecta e agencia essa diversidade. Na medida em que a cartografia traça esse plano comum e heterogêneo, ela concorre para a construção de um mundo comum.

Desse modo, o dispositivo revisão utilizado para operar a cartografia aqui esboçada não está comprometido com a produção de categorias de identidade dos trabalhos com crianças em Educação Matemática, mas, ao contrário, com a conexão de heterogêneos que encontram sua comunidade em determinados pontos, com o plano que articula, conecta e agencia a diversidade de pesquisas com crianças produzidas na área.

Dois pontos constituem políticas de funcionamento desta revisão: primeiro, a produção dos planos comuns discutidos neste artigo, e não outros quaisquer. Segundo, a indicação de que procuramos periódicos de peso histórico para a Educação Matemática, bem como trabalhos do GT 01 da SBEM. Quanto ao primeiro ponto, destacamos que a produção dos planos comuns aqui discutidos diz de um certo modo de abordar o conceito da infância a partir da noção de devir-criança de que falamos brevemente na seção anterior. Assim sendo, há o interesse por compreender como as pesquisas em Educação Matemática vão produzindo sua compreensão singular da infância e da produção do conhecimento pelas crianças. Quanto ao segundo ponto, a cartografia aqui traçada foi produzida de modo a ocupar-se, por um lado, dos espaços institucionais da Educação Matemática nos quais a infância é intencionalmente colocada como objeto de pesquisa – por isso a revisão de trabalhos ligados ao GT01 da SBEM – e, por outro, ocupar-se de espaços cujos estratos históricos sejam amplamente reconhecidos na área – por isso a revisão em periódicos mais tradicionais e reconhecidos. Interessa-nos, com esses dois pontos, afirmar as singularidades dos modos de compreensão já reconhecidos na área, dando relevo a seu caráter radicalmente produzido. Com isso, operamos numa contra naturalização das compreensões de infância que se estratificam em alguns dos espaços mais hegemônicos da Educação Matemática, apontando para a necessidade de recolocar o problema da infância na área e produzir tantos outros modos de compreendê-la, ou seja, de afirmar seu caráter inventivo e inventado (Kastrup, 2007).

Para a seleção dos artigos, buscamos todas as pesquisas publicadas em um determinado período de tempo nos periódicos e revistas através dos critérios: primeiramente, para os periódicos considerou-se apenas artigos, excluindo de saída relatos de experiência, resenhas e trabalhos em outros idiomas, enquanto para os eventos considerou-se todos os anais de antemão, realizando posteriormente um filtro que considerava apenas os artigos; após isso, fizemos a leitura dos títulos, seguida imediatamente da leitura dos resumos. Procuramos os artigos que possuíam em seus títulos palavras ou expressões que sinalizassem um estudo sobre Educação Matemática na infância. Para esse recorte, consideramos pesquisas com crianças até o fim dos anos iniciais do Ensino Fundamental. Por fim, foi feita a leitura dos artigos remanescentes. Nas Tabelas 1 e 2 a seguir constam o período de tempo averiguado nos periódicos e anais de eventos analisados e os artigos, divididos por publicação, selecionados após a filtragem.

Tabela 1. Período de Tempo Analisado para a Seleção dos Artigos

Publicação	Período abordado
Bolema	2012 - 2022
ENEM4	2019 - 2022
GEPEM5	2012 - 2022
Perspectivas da educação matemática6	2011 - 2022
SIPEM7	2015 - 2022
Zetetiké	2012 - 2022

Tabela 2. Artigos Selecionados por Publicação

Publicação	Número de artigos selecionados
Bolema	14
ENEM	8
GEPEM	7
Perspectivas da educação matemática	18
SIPEM	9
Zetetiké	4

Fuente: Elaboración propia

Foram excluídos os trabalhos que não apresentaram explicitamente a temática da educação matemática na infância no título ou no resumo. A partir do corpus inicial de trabalho, 60 artigos foram selecionados para constar nesta revisão sistemática de literatura.

Uma primeira leitura dos trabalhos revelou que, entre os 60 artigos examinados, predominantemente, 15% abordam conteúdos relacionados com sentido numérico, 11,7% com resolução de problemas, 10% modelagem matemática, 8,3% estatística, 6,7% jogos e o restante se divide entre outros temas como relatos de estudantes, cálculo mental e geometria.

Figura 1. Distribuição de Trabalhos Revisados por Assunto Predominante

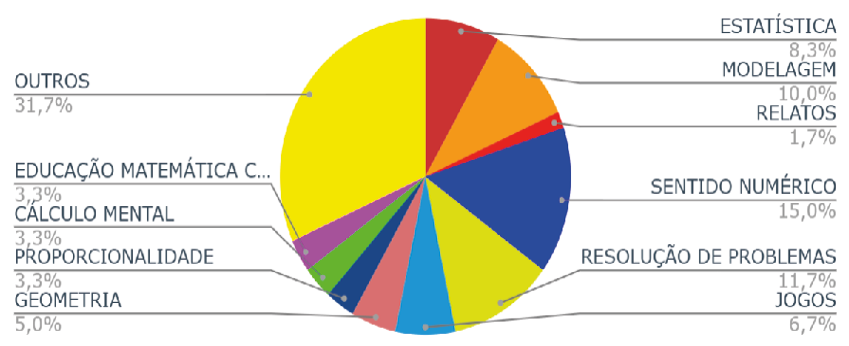
Fuente: Elaboración propia

Infância e crianças na pesquisa em Educação Matemática: alguns planos comuns

Passamos a discutir os planos comuns aos trabalhos que revisamos. O primeiro deles trata de uma forte influência cognitivista, mais especificamente, de influência piagetiana. Piaget (1974; 1993) classifica o desenvolvimento cognitivo das crianças em estágios: o sensório-motor, o estágio pré-operatório, operatório concreto e operatório formal.

Tal perspectiva parte de uma certa normalidade do percurso de desenvolvimento infantil, de uma caracterização dessa normalidade por meio de um caminho necessário de desenvolvimento e dos invariantes operacionais que caracterizam os estágios de desenvolvimento. Toda a caracterização do construtivismo parte dessa ideia dos invariantes, então, uma vez que se estabelece esses invariantes, por conseguinte, estabelece também um critério da normalidade. A partir disso, é possível prever qual caminho a criança vai seguir para aprender conteúdos matemáticos, assim como consegue dizer para qual conceito um certo invariante aponta.

Desta forma, na visão construtivista, como cada estágio corresponde a um período de idade diferente, é possível prever tudo o que a criança faz (ou o que se espera que ela faça) e, também, é possível situar o que ela fala e o que ela faz dentro desse esquadrinhamento que já é conhecido e definido pelos adultos. Portanto, o que a criança faz pode ser sempre efetivamente rebatido por um dos estágios, o que acaba por estabelecer o critério de verdade. Além disso, apesar de cada estágio ser definido por características próprias, a criança sempre é comparada ao adulto, sendo pensada pela ausência, pela falta de características próprias dos adultos.

Nesse sentido, cria-se uma Educação (Matemática) em que não há preocupação com o que a criança procura estabelecer de novo, mas sim em procurar em que momento do desenvolvimento está o que ela faz. Em particular, preocupa-se com a matemática que está subentendida na ação infantil para identificá-la em um quadro de referência que fornece os parâmetros para saber como lidar com ela. Assim, cria-se uma Educação (Matemática) em que se pode antecipar tudo o que acontece no encontro da criança com a matemática, não sobrando quase nada que aponta para o novo, para o inesperado. Dessa forma, relega-se a um quadro de referência qualquer problema que a criança inaugure que venha a ser uma máquina produtiva de desejo. Nesse sentido, Cammarota apresenta duas proposições sobre essa educação (matemática): “Primeira, uma educação (matemática) impede ou procura impedir toda a produção do desejo e, com ela, toda a produção (matemática); segunda, uma educação (matemática) impede ou procura impedir a formação de enunciados” (Cammarota, 2021, p. M-17).

É nesse sentido que o artigo de Mandarino (2022) fundamentou-se em referenciais teóricos inspirados nas ideias de Piaget que destacam as ações mentais essenciais para a formação do conceito de número racional. Ao analisar as atividades realizadas pelas crianças, o estudo concentrou-se em identificar ações que contribuíram para a introdução do processo de construção do conceito de número racional. Nesse contexto, foram exploradas cinco das sete condições descritas por Piaget como fundamentais e necessárias para a compreensão do conceito de fração:

(A) a existência de uma totalidade divisível – “o inteiro”; (B) existência de um número determinado de partes – total do número de partes em que o inteiro está dividido; (C) esgotamento do todo – não é possível haver resto; (D) igualização das partes – a divisão fracionária implica na obtenção de partes iguais, sejam elas discretas ou contínuas; (E) atendimento ao princípio da invariância: a soma das frações constituídas é igual ao todo inicial – ao considerarmos todas as partes em que o inteiro foi dividido, voltaremos a obter esse inteiro. (Mandarino, 2022, p. 5-6)

O trabalho de Pavanello e Costa (2018) também adota uma abordagem teórica subjacente baseada na perspectiva sócio-construtivista com raízes na teoria de Piaget.

Outro plano comum que traçamos aqui é a captura da categoria de aluno sobre as crianças, ou seja, a concepção de aluno da instituição escola se sobrepõe à ideia de criança e de infância. Essa captura, apesar de sutil, não é por acaso. Quando o aluno chega antes da criança, ela já é considerada uma criança da instituição escola, ou seja, o aluno já está lido pela escola, já se sabe como ele deve se portar, como deve aprender e de que maneira se pode intervir na criança. É a institucionalidade que faz a criança: não existe criança fora da instituição, ela já é imediatamente institucionalizada. Mas não só isso, a categoria de aluno é historicamente constituída com os objetivos de aprendizagens e disciplinas específicas e aquisição de valores e saberes comuns.

A instituição escolar, de certo modo, apaga a criança como sujeito concreto, dando lugar ao aprendiz, cujas ações e comportamentos são prescritos e avaliados de acordo com os padrões adultos. Essa realidade levanta questões importantes sobre a necessidade de considerar a singularidade da criança em ambientes educacionais. Também nos chama a atenção para o desafio de encontrar um pensar a função escolar de preparação das crianças para o mundo acadêmico e o incentivo à sua curiosidade, criação e capacidade de explorar o novo e o inesperado na matemática.

Nesse contexto, podemos mencionar os conceitos de ofício do aluno e ofício da criança (Marchi, 2010). Quando esses conceitos se encontram no contexto escolar, eles remetem a processos de criação e modelagem de programas, regras, instrumentos e práticas pedagógicas que fazem da escola o espaço central da criança. A escola se torna o local onde a criança é esperada a exercer seu ofício e a se comportar de acordo com a definição socialmente atribuída à infância. Esse processo implica, desde a primeira infância, a inserção da criança em papéis institucionais predefinidos, evidenciando o cerne da institucionalização da infância. Isso representa um movimento de criação e racionalização de atividades para esse período da vida, culminando na construção social da norma moderna da infância e do comportamento infantil (Marchi, 2010).

O “ofício de aluno” pode ser definido antes de tudo como a “aprendizagem das regras do jogo” escolar. Ser “bom aluno” não é somente assimilar conhecimentos, mas também estar disposto a “jogar o jogo” da instituição escolar e estar disposto a exercer um papel que revela tanto conformismo quanto competência. Assimilar o currículo, não somente o formal, mas também o chamado “currículo oculto” (onde se aprendem as regras não explícitas, mas igualmente necessárias da cena pedagógica) é tornar-se um “nativo da cultura escolar”, capaz de desempenhar o “papel de aluno” sem perturbar a ordem institucional nem demandar atenção particular. (Marchi, 2010, p. 191)

Ainda nessa problemática, dentre os artigos analisados, é possível notar que a palavra criança é mencionada poucas vezes ao longo dos textos. Por exemplo, em Conceição e Rodrigues (2019),a palavra criança é usada apenas uma vez em relação a uma citação que afirma: “De acordo com Clements e Sarama (2014), as crianças têm a capacidade de utilizar translações, reflexões e rotações desde os cinco anos, embora inicialmente somente no contexto da manipulação de materiais” (Conceição & Rodrigues, 2019, p. 41). Entretanto, ao longo do restante do artigo, o termo adotado é alunos, conforme o enfoque do estudo:

Este artigo pretende aprofundar o conhecimento acerca do processo de estruturação espacial de alunos do 1.º ano do Ensino Básico, analisando estratégias utilizadas por duas alunas na realização de duas tarefas, uma centrada na construção e desenho e outra na reprodução com materiais manipuláveis de figuras bidimensionais. (Conceição & Rodrigues, 2019, p. 37)

Por fim, observa-se regularmente nos textos lidos que a Educação Matemática vem apostando cada vez mais na antecipação do uso de ferramentas didático-metodológicas com crianças cada vez mais novas, em prol de um discurso de que elas aprenderiam melhor matemática no futuro. Destacam-se trabalhos com educação estatística e modelagem matemática na Educação Infantil. Esta aposta provoca algumas preocupações. Assim como no Mito Pedagógico dos Gregos (Kohan, 2003) em que a criança era uma expectativa de futura pólis, hoje essa antecipação aponta para uma expectativa de que a criança participe da semiótica capitalista não só no futuro, mas desde já, colocando desde cedo em jogo ideias como a de produtividade máxima e competitividade. A aposta é na antecipação do que Guattari (1977) chama de iniciação aos valores da semiótica dominante. Então, não se trata apenas de dizer o que a criança deve aprender na Educação Infantil, mas também, na maneira que isso é feito, se estabelece um exercício de poder sobre as crianças, ou seja, é uma maneira de moldar os desejos das crianças para que eles operem dentro das semióticas dominantes. No campo da Educação Matemática, nos interessa pensar, então, como contribuímos com parte desse exercício de poder sobre as crianças ou como resistimos a ele.

A insistência na produtividade traz consigo um pressuposto de que a brincadeira da criança só é produtiva quando há um objetivo de aprender algum conteúdo, neste caso, matemático. Nesse sentido, observamos que a maioria dos textos analisados que traziam atividades matemáticas com crianças eram sempre com atividades lúdicas e com brincadeiras procurando se conectar com o mundo infantil. Entretanto, há um risco de entender o que a criança faz, sua brincadeira e sua experimentação com o mundo em que não haja nenhum objetivo dado de antemão como algo que não é produtivo e nem faz parte do aprendizado da criança.

Se a concepção de criança está impregnada por uma visão reducionista, especialmente ao considerarmos que essa antecipação da escolarização é consequência de uma política dominante capitalista e segregacionista, podemos concluir que o brincar passa a ser visto como uma atividade não prioritária, mas de função disciplinar e didatizada e não como relevante para o desenvolvimento integral da criança, uma vez que se preocupa com conteúdos a serem ensinados e não com o eixo de trabalho, além de ser uma atividade explorada como se fosse separada da construção do conhecimento e da própria construção da linguagem, condizente com uma visão dualista da criança. (Barros, 2009, p. 54).8

Dessa forma, o brincar não está no centro da vida escolar das crianças, mas sim a necessidade de preparação e de construção de uma base de conhecimento para o Ensino Fundamental, subsume-se a noção de criança na noção de aluno. Como aluno, as brincadeiras não são mais uma prioridade, apenas na medida que algo possa ser ensinado. A Educação Infantil torna-se refém desta transmissão de conteúdos. Apenas o uso de terminologias como conteúdos já é de certa preocupação nesta etapa da Educação Básica, já que revela essa necessidade de inserir as crianças em um contexto de preparação para o Ensino Fundamental.

Nesse sentido, parece ignorar que o brincar é uma prática legítima da criança e faz parte da sua experimentação com o mundo, é um modo de estar no mundo. O brincar por si só já faz parte dessa experimentação e, portanto, do aprendizado das crianças e não pode ser reduzido a apenas reprodução de conteúdos, caso contrário ela perde seu sentido, seu sentido de potência própria, de criação e invenção da criança.

Neste plano comum, Dias et al (2020) partem da seguinte indagação como ponto de partida: é possível ensinar Estocástica9 na Educação Infantil?. O artigo argumenta que, à primeira vista, ensinar estocástica para crianças na primeira etapa da Educação Básica pode parecer inviável, mas que a teoria de aprendizagem de Bruner sustenta que é possível transmitir qualquer conteúdo de forma adequada a crianças de todas as idades.

Além disso, o artigo de Kian et al. (2022), adota uma abordagem que considera essencial o estudo de conceitos probabilísticos a partir dos anos iniciais da formação da criança com o argumento de que, na sociedade atual, somos constantemente bombardeados com uma grande quantidade de informações, tornando necessário o entendimento de fenômenos aleatórios e não aleatórios. O artigo também menciona como inspiração a Base Nacional Comum Curricular (BNCC), que ressalta a necessidade de incentivar a formação de conceitos relacionados à probabilidade desde os primeiros anos do Ensino Fundamental.

Considerações finais

A produção de planos comuns aos textos lança luz sobre aspectos significativos da pesquisa em Educação Matemática na infância. Primeiro, identifica-se um plano comum entre eles, que consiste na falta de uma discussão do que compreendem por criança e infância, o que indica a necessidade de maior reflexão sobre esses conceitos essenciais para a pesquisa. Além disso, destaca-se que a categoria de aluno frequentemente se sobrepõe à noção de criança, o que molda as crianças de acordo com as expectativas educacionais mesmo na Educação Infantil. A influência cognitivista, especialmente a abordagem piagetiana, é evidente nos estudos de educação matemática na infância, enfocando a abordagem de pesquisa por meio da noção de desenvolvimento cognitivo. No entanto, essa perspectiva tende a homogeneizar a produção matemática das crianças, ignorando ou reduzindo diferenças e as influências sociais e culturais. Por fim, destaca-se a crescente ênfase na antecipação do uso de ferramentas didáticas com crianças cada vez menores, especialmente na educação estatística e modelagem matemática na Educação Infantil.

Portanto, a pesquisa aponta para a necessidade de repensar a forma como a Educação Matemática é concebida, a fim de permitir que a atividade matemática de crianças possa ser pensada a partir de uma perspectiva da invenção. A perspectiva do devir-criança, inspirada na filosofia de Deleuze e Guattari, nos auxilia nessa proposta e destaca a importância de reconhecer a infância como uma dimensão sempre contemporânea, uma criação constante que persiste na vida adulta. Isso nos leva a repensar a relação entre adultos e crianças, enfatizando a necessidade de ouvir e valorizar as crianças em nossa sociedade. Esta cartografia nos instiga a não apenas examinar os planos comuns e as tendências predominantes nos trabalhos revisados, mas também a pensar os escapes, ou seja, aquilo que foge aos planos comuns que traçamos aqui na pesquisa em Educação Matemática. Esta tarefa de cartografar os escapes está em curso no contexto da pesquisa mais ampla.

À luz dessas reflexões, este estudo busca contribuir para uma Educação Matemática que reconheça a capacidade das crianças de produzir conhecimento matemático, que valorize a infância como uma condição da experiência humana, e que promova o diálogo e a escuta das crianças. Esta cartografia não se encerra aqui. Ela nos convida a continuar explorando as complexidades da infância e da Educação Matemática e a repensar nossas práticas e abordagens de pesquisa, ou seja, nossas práticas de saberes, poderes e (des)subjetivação na relação com as crianças.

Declarações finais

Contribuição dos autores. Este trabalho foi produzido de maneira dialogada entre os três autores utilizando a produção de dados construída pelos três para a execução do projeto de pesquisa coordenado pelo primeiro autor e no âmbito do qual as duas autoras atuam como bolsistas de Iniciação Científica.

Conflito de interesses. Não há conflito de interesses a serem relatados.

Financiamento. O projeto de pesquisa Crianças e matemáticas em produção na (pré)escola: cartografias de uma infância da (educação) matemática, a partir do qual se origina este trabalho, é financiado pelo Programa Institucional de Bolsas de Iniciação Científica da Universidade Federal de Juiz de Fora.

Implicações éticas. Não há implicações éticas a serem relatadas.

Referências:

Agamben, G. (2001). Infância e história. Belo Horizonte: Editora UFMG.

Andrade, C. (2008). Contos de aprendiz. Rio de Janeiro: Record.

Ariés, P. (1981). História social da criança e da família. Rio de Janeiro: Livros Técnicos e Científicos.

Barros, F. (2009). Cadê o brincar? Da educação infantil para o ensino fundamental. São Paulo: Cultura Acadêmica.

Barros, M. (2010). Poesia Completa. São Paulo: Leya.

Cammarota, G. (2021). Fascículos de experiências: rastros de um estudo com crianças e matemáticas, inventividade e cultura ou pesquisar em modo João. [Tese de Doutorado, Universidade Estadual Paulista “Júlio de Mesquita Filho” – Campus Rio Claro]. Repositório Institucional https://repositorio.unesp.br/handle/11449/215222. Acesso em: 2 set. 2023.

Conceição, J. & Rodrigues, M. (2019). Estratégias de estruturação espacial utilizadas por alunas do 1. º ano na construção e reprodução de figuras bidimensionais. Boletim GEPEM, (74), 37–55. http://dx.doi.org/10.4322/gepem.2019.004

Deleuze, G. (1996). O abecedário de Gilles Deleuze: transcrição integral do vídeo. CLINICAND. http://clinicand.com/wp-content/uploads/2021/02/Gilles_Deleuze_Claire_Parnet_Abeced_rioz-lib.org_.pdf

Deleuze, G, & Guattari, F. (2011a). O anti-édipo: capitalismo e esquizofrenia 1. São Paulo: Editora 34.

Deleuze, G, & Guattari, F. (2011b). Mil Platôs: capitalismo e esquizofrenia 2 (Volume 1). São Paulo: Editora 34.

Deleuze, G, & Guattari, F. (1997). Mil Platôs: capitalismo e esquizofrenia 2 (Volume 4). São Paulo: Editora 34.

Deligny, F. (2015). O aracniano e outros textos. São Paulo: n-1 Edições.

Dias, C. et al. (2020). É possível ensinar Estocástica para crianças da Educação Infantil? Uma análise à luz da Teoria de Bruner. Bolema: Boletim de Educação Matemática, 34(66), 157-177. http://dx.doi.org/10.1590/1980-4415v34n66a08

Foucault, M. (2017). Microfísica do poder. Rio de Janeiro: Paz & Terra.

Guattari, F. (1977). Revolução Molecular. São Paulo: Brasiliense.

Galvão, M. (2019). Revisão sistemática da literatura: conceituação, produção e publicação. Logeion: Filosofia da informação 6(1), 57-73. http://dx.doi.org/10.21728/logeion.2019v6n1.p57-73

Kastrup V. (2007). A invenção de si e do mundo: uma introdução do tempo e do coletivo nos estudos da cognição. Belo Horizonte: Autêntica.

Kastrup, V. & Barros, R. (2009). Movimentos-funções do dispositivo na prática da cartografia. In Passos, E. et al. (Org.), Pistas do método da cartografia: pesquisa-intervenção e produção de subjetividade (pp. 76-91). Porto Alegre: Sulina.

Kastrup, V. & Passos, E. (2013). Cartografar é traçar um plano comum. Fractal Revista de Psicologia, 25(2), 263-280. https://doi.org/10.1590/S1984-02922013000200004.

Kian, F., Júnior, A. & Santos, L. (2022). A identificação por alunos do quinto ano do ensino fundamental, entre eventos aleatórios cotidianos, aqueles que se configuram como impossíveis. In Anais do XIV Encontro Nacional de Educação Matemática. https//www.even3.com.br/anais/xivenem2022/479551.

Kohan, W. (2003). Infância. Entre Educação e Filosofia. Belo Horizonte: Autêntica.

Mandarino, S. et al. (2022). Números racionais nos anos iniciais – despertando para uma nova ideia de números. In Anais do XIV Encontro Nacional de Educação Matemática. https//www.even3.com.br/anais/xivenem2022/478257.

Marchi, R. (2010). O “ofício de aluno” e o “ofício de criança”: articulações entre a sociologia da educação e a sociologia da infância. Revista Portuguesa de Educação, 23(1), 183-202. http://dx.doi.org/10.21814/rpe.13983

Pádua, G. (2009). A epistemologia genética de Jean Piaget. Revista FACEVV, (2), 22-35.

Pavanello, R., Costa, L. (2018). Geometria e educação infantil: o que dizem os pesquisadores?. In Anais do VII SIPEM - Seminário Internacional de Pesquisa em Educação Matemática.http://www.sbemparana.com.br/eventos/index.php/SIPEM/VII_SIPEM/paper/view/397/356.

Piaget, J. & Inhelder, B. (1974). A psicologia da criança. Rio de Janeiro: Difel.

Piaget, J. (1993). Seis estudos de psicologia. Rio de Janeiro: Forense.

Rolnik, S. (2016). Cartografia sentimental: transformações contemporâneas do desejo. Porto Alegre: Sulina.

Vergnaud, G. (1996). A Teoria dos Campos Conceituais. In Brun, J. (Ed.), Didática das Matemáticas (pp. 155-191). Lisboa: Instituto Piaget.

---