Introducción1

La Licenciatura en Matemáticas de la Universidad Pedagógica y Tecnológica de Colombia2 [UPTC], como pionera en la formación de docentes en Colombia, a través de sus diferentes etapas y nombres, tiene una historia de noventa años de formación de profesionales en la enseñanza de las matemáticas. Analizar elementos de la evolución histórica del programa para conocer las reformas que se le han hecho podrá dar luces que ayuden a comprender la propia formación de profesores de matemáticas. El hecho de no existir documentos históricos específicos consistentes e integrados que rescataran la evolución del programa se convertía en una carencia para el mejoramiento del mismo, ya que no hay la posibilidad de aprender del pasado, de los aciertos, de los errores y de las dificultades presentadas. La investigación que aquí se reporta tuvo como objetivo identificar elementos que evidencien etapas en la evolución histórica del currículo de la Licenciatura en Matemáticas, perfiles de formación y estructura y funcionalidad de los planes de estudios en diferentes periodos, así como los principios pedagógicos implícitos en el trabajo docente. Este texto reporta el periodo comprendido entre los años 1929 a 2000.

La formación de profesores de matemáticas.

Esta es un área dinámica de investigación en los últimos años, si bien no la suficiente, ya que en el aula de clase la modificación de las prácticas sigue siendo un problema a resolver (Jiménez & Gutiérrez, 2017). Por un buen tiempo, la formación y la investigación se centraron en qué tipo de contenidos debía dominar el futuro profesor. Tal vez fue Shulman (1986) el primero en destacar que además del conocimiento matemático, es indispensable el conocimiento didáctico pedagógico del contenido y el del currículo, lo cual permite ya distinguir al profesor de un especialista en contenidos disciplinares, pues vincula los contenidos a la enseñanza y al aprendizaje. De la misma forma, Ponte (2001) destaca la necesidad de ese otro tipo de contenidos y afirma: “si para ser profesor de matemática se necesita saber matemática, no es menos verdadero que […] necesita un conocimiento profesional que incluye aspectos diversos, desde el conocimiento didáctico al conocimiento del currículo y de los procesos de aprendizaje” (p. 11).

Ball, Thames & Phelps (2008) describen de una forma particular lo que pasa en la formación inicial de profesores de matemáticas, al afirmar que desafortunadamente en la formación tradicional los cursos tienden a ser académicos en el mejor y el peor sentido de la palabra, académicos e irrelevantes, de cualquier manera alejados de la enseñanza en el aula. Estos autores parten de los trabajos de Shulman (1986, 1987) e indagan sobre las particularidades que tendría el conocimiento del contenido específico para la enseñanza. Asimismo se preguntan qué hacen los profesores al enseñar y qué necesitan saber para hacerlo efectivamente. Su foco de estudio está en una descripción detallada del trabajo docente efectivo. Ponen el énfasis en el uso del conocimiento en y para la enseñanza e intentan identificar tareas y problemas recurrentes en la enseñanza de las matemáticas. Sientan las bases para una práctica basada en una teoría del “conocimiento matemático para la enseñanza” (p. 395), con lo cual quieren expresar el conocimiento matemático necesario para llevar a cabo el trabajo de enseñanza de las matemáticas y lo que esto implica; en otras palabras, el conocimiento matemático necesario para realizar las tareas recurrentes de la enseñanza de las matemáticas a los alumnos.

En el análisis del conocimiento matemático para la enseñanza, identifican tres dominios. El primero se refiere a la comprensión de las matemáticas dentro del currículo, ya que juega un papel central en la planificación y la ejecución de la enseñanza. El segundo, el conocimiento especializado del contenido [SCK], es el conocimiento matemático y la habilidad única de la enseñanza, o conocimiento del contenido y su enseñanza. Un examen detallado revela que el SCK es un conocimiento matemático especializado, que “no suele ser necesario para fines distintos de la enseñanza” (Ball et al., p. 396). Las demandas del trabajo de enseñar matemáticas crean la necesidad de un cuerpo de conocimiento matemático especializado para la enseñanza. El tercer dominio, el conocimiento del contenido y los estudiantes, implica conocer la relación de los estudiantes con las matemáticas. Aquí los maestros deben anticipar qué es probable que piensen los estudiantes y qué encontrarán fácil, difícil o confuso; anticiparse a lo que es probable que hagan y además ser capaces de escuchar e interpretar el pensamiento emergente e incompleto de los estudiantes, tal como lo expresan los alumnos en sus formas y lenguaje usual. Ball et al. destacan que estudiar las relaciones entre el conocimiento del contenido para la enseñanza y los logros de sus estudiantes sería útil para determinar si hay aspectos del conocimiento de los maestros que predicen el rendimiento de los estudiantes y comprender las dimensiones más importantes de los conocimientos profesionales de los profesores. Ese conocimiento especializado para enseñar matemáticas requiere más investigación para entender las dimensiones del conocimiento profesional de los profesores de matemáticas.

Carrillo (2014) ve al futuro maestro, no como un especialista en el contenido matemático, sino como alguien con un conocimiento especializado sobre su enseñanza. Con base en Ball et al. (2008) propone el modelo conocimiento especializado del profesor de matemáticas, el cual intenta trascender la diferencia entre conocimiento común y especializado, y superar las dificultades de limitación entre los subdominios del conocimiento especializado en matemáticas y conocimiento del contenido pedagógico y de los estudiantes. A lo propuesto por Ball et al. (2008), Carrillo (2014) añade el estudio de las creencias del profesor sobre las matemáticas, su enseñanza y aprendizaje. A pesar de las reformas a los planes de formación de profesores, en la mayoría de casos las áreas permanecen disyuntas. La formación disciplinar matemática continúa en manos de matemáticos y la pedagógica en los pedagogos, y de esta forma “permanece, a pesar de todo, el problema de la integración con la práctica” (Cavalcante & David, 2007, p. 14).

Para sobreponerse a esa separación, se requiere integrar esas áreas. Fiorentini y Creci (2017) destacan que el saber ser y el saber hacer del profesor —el saber de la práctica— no se transforma por la simple aplicación de conocimiento teórico, sino por la posibilidad de la problematización de las prácticas de aprender y enseñar matemáticas, sin olvidar la referencia a los conocimientos producidos en la investigación. De aquí se desprende que en la formación inicial los estudiantes deberían vivenciar un proceso continuo de investigación en el medio escolar desde la observación y problematización de las prácticas.

Como lo manifiestan Ball et al. (2008), es necesario comprender cómo aprenden los maestros, con qué oportunidades, bajo qué condiciones y cómo mejorar las posibilidades de aprender. De acuerdo con lo anterior, investigaciones recientes (Riscanevo & Jiménez, 2017a) destacan las oportunidades de aprendizaje del profesor a través de la vinculación a comunidades o grupos, dada la complejidad, no solo del aula, sino del propio aprendizaje de los profesores, que son influenciados por factores personales, sociales, culturales y políticos. Enfatizan en los diseños de entornos específicos para el aprendizaje del profesor, donde se pueda percibir la relación entre cognición situada y comunidades de práctica o comunidades de aprendizaje. Esta relación asume el carácter integrado del conocimiento del profesor, ya que el conocimiento se genera a través de la experiencia práctica vinculada a problemas concretos de la misma. Para el caso de la formación inicial, el ambiente de aprendizaje debe posibilitar que el estudiante viva durante su formación una verdadera experiencia de aprendizaje, con base en la reflexión e investigación de la práctica de enseñar matemáticas en la escuela.

Las creencias del profesor.

Se refieren a construcciones mentales personales y subjetivas y que son difíciles de modificar (Schoenfeld, 1998). Cualquier acción educativa se hace con base en unas creencias y unas concepciones de tipo filosófico, epistemológico, pedagógico y sobre aspectos básicos del área de estudio, o sobre la estructura que debe tener una clase, la mayoría de las veces implícitas y no analizadas por los propios profesores, como por ejemplo, sobre la propia matemática o comunicación en la clase (Jiménez, 2010; Jiménez, Suárez & Galindo, 2010).

Según Santos (1993), la mayoría de docentes de matemáticas las ve tan solo como un conjunto de algoritmos, procedimientos o reglas que el estudiante debe memorizar, para resolver ejercicios y problemas presentados por el profesor y tomados de un texto guía. De la misma forma se desconoce la esencia de la clase de matemáticas como oportunidad para el desarrollo del pensamiento lógico y argumentativo (Pachón, Parada & Chaparro, 2016). En el mismo sentido, Tardif (2013), a partir de varios estudios, dice que la mayoría de docentes reproducen en el aula las prácticas pedagógicas de sus predecesores de hace más de un siglo, problema aún vigente (Jiménez, Limas & Alarcón, 2016).

Metodología

La investigación es un estudio de caso, de enfoque cualitativo, con análisis de documentos y entrevistas no estructuradas. Según Corbetta (2007), “los documentos institucionales reflejan exactamente lo que su definición sugiere, es decir, la dimensión institucional de los fenómenos estudiados” (p. 403). Se entrevistaron tres profesores del programa, dos ya pensionados y otro aún en ejercicio. Se consultaron documentos históricos como folletos, boletines, informes, proyectos, normas, acuerdos y decretos hallados en el Archivo Histórico de la Escuela Normal Superior Santiago de Tunja, Archivo Histórico de la Facultad de Educación (UPTC), documentos varios de la Escuela de Matemáticas y Estadística y de la Licenciatura en Matemáticas.

El estudio de caso es un método naturalista que interpreta los datos observados, y como en toda la investigación cualitativa, su validez recae en la responsabilidad del investigador, y se centra en estudiar en profundidad un determinado ejemplo o caso (Martínez, 1988).

En la primera etapa de la investigación se revisaron y analizaron en detalle documentos escritos. En la segunda, con base en estos resultados se hicieron entrevistas, de tal manera que a través de la memoria oral3(Rodríguez, 2004) se tuviera un mayor conocimiento histórico del programa. En la tercera etapa, la información se organizó, clasificó, analizó y trianguló, para hacer una descripción de las distintas etapas de la evolución histórica del currículo del programa y de aspectos complementarios. Los planes de estudio se esquematizaron en tablas, para poder comparar y destacar aspectos relevantes.

Resultados y discusión

En el periodo 1928-2000, se identificaron once planes de estudio del curso histórico de la licenciatura y de cada uno se destacaron las características centrales y más notables, en todas las áreas, para identificar diferencias entre una y otra época, entre uno y otro plan de estudios. La información se clasificó en tres categorías de análisis: los planes de estudio, los perfiles de formación, y la metodología de aula.

El programa de Licenciatura en Matemáticas de la UPTC nace —aún sin este nombre— dentro del llamado Curso Suplementario de Especialización Legalizada en 1928, como una sección de la Escuela Normal Superior de Tunja. Pretendía formar profesores en matemáticas y en ciencias básicas para la educación media normalista —formadora de profesores de la educación básica en general—. Según las tendencias en cada época, fueron apareciendo modificaciones, tanto en el área disciplinar matemática como en las áreas pedagógica y general.

La formación de docentes de matemáticas en los albores de la Facultad de Educación.

La primera Facultad de Educación del país —que más tarde se convertiría en la Universidad Pedagógica de Colombia y posteriormente en Universidad Pedagógica y Tecnológica de Colombia— nace como consecuencia de dos hechos fundamentales: el primero, la llegada al país de las ideas renovadoras de la escuela nueva, que nace en Europa a comienzos del siglo XIX, como un movimiento que plantea la transformación de la escuela, y toma al alumno como centro de la acción educativa; y el segundo, la necesidad de formar profesores con espíritu renovador centrado también en la escuela nueva. El otro hecho fue la influencia que tuvieron las misiones alemanas traídas al país; la primera para la creación de las escuelas normales hacia 1870 (Archivo Escuela Normal Superior Santiago de Tunja) y la segunda, hacia 1925, con el fin de reestructurarlas4.

En la Escuela Normal de Tunja, Sieber organizó el primer Curso Suplementario de Especialización con una duración de dos años y pretendía formar maestros en matemáticas, física y química. Para el área de matemáticas, las materias de estudio eran: geometría, trigonometría, geometría analítica, algebra, cálculo diferencial e integral, logaritmos y regla de cálculo, empleo de papeles milimétrico, logarítmico y semilogarítmico (Parra, 2003).

Según el Libro de Exámenes, Grados y Premiaciones del Curso de Especialización para Profesores de Enseñanza Secundaria, anexo a la Escuela Normal, los tres primeros graduados de este curso fueron José Estiliano Acosta Gómez, Juan N. Segura y Florentino Cortés. Para 1932 los graduados fueron Mardoqueo Santamaría y Santos A. Pinzón (Archivo Histórico Escuela Normal Superior Santiago de Tunja).

Los planes de estudio de la licenciatura en diferentes épocas.

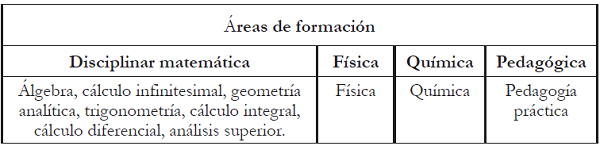
A continuación se presentas planes de estudio, donde se destacan los énfasis que pretendía cada plan. El primer plan de estudios (tabla 1) estaba dirigido a la enseñanza secundaria y normalista de esa época. El perfil era en realidad el de un profesor de ciencias básicas —matemáticas, física y química—, enfatizando más en matemáticas. En el área pedagogía se destacan las prácticas supervisadas. No se encontraron evidencias de intensidades horarias ni porcentajes por áreas (Gómez & Moreno, 2006).

Tabla 1

Plan 1928; Curso Suplementario de Especialización Legalizada.

Elaboración propia.Tabla 1 Después de cierres en diferentes momentos y traslado de sede, debidos a causas políticas diversas, a través del Decreto 2655 del 10 de octubre de 1953 se crea oficialmente la Universidad Pedagógica de Colombia, institución universitaria oficial de orden nacional. El plan de estudios de 1954 se puede ver en la tabla 2. En este plan el enfoque disciplinar permite observar que sigue dirigido a la educación media. La fundamentación pedagógica en las áreas específicas —aritmética, álgebra, geometría y física— era bastante detallada. Existían cursos de metodología de cada una de estas. En el área general, con el curso de cultura religiosa se percibe la influencia de la Iglesia en la formación de maestros. Desde este año y durante mucho tiempo, la universidad fue solo pedagógica y existieron varias facultades, como se puede ver aquí, al mencionar la Facultad de Matemáticas y Física.

Tabla 2

Plan de estudios, 1954

Elaboración propia.5.Tabla 2 El siguiente plan encontrado es de 1955, en el que no hay gran diferencia con el plan anterior de 1954. Disminuye la suma horaria total, pasa de 3744 a 3424 horas. Se destaca que el área de formación en matemáticas aumenta un 2.77%, el área de formación en física disminuye un 0.64%, al igual que disminuye ligeramente el área de formación pedagógica. El perfil profesional continúa siendo de un maestro para educación media (tabla 3).

Tabla 3

Plan de Estudios, año 1955

Elaboración propia.Tabla 3 En el plan de 1956 se amplía la formación en geometría y trigonometría del plano al espacio. Sin embargo, porcentualmente la formación disciplinar matemática disminuye, al igual que en química. Se incrementan sustancialmente los estudios en física y cambia su denominación —incluyendo sus prácticas—. En el área disciplinar no aparece la estadística. En el área pedagógica no se evidencian mayores variaciones. El perfil profesional continúa igual.

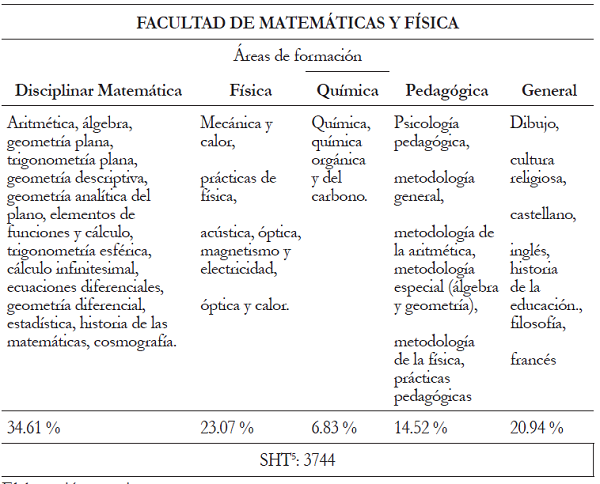
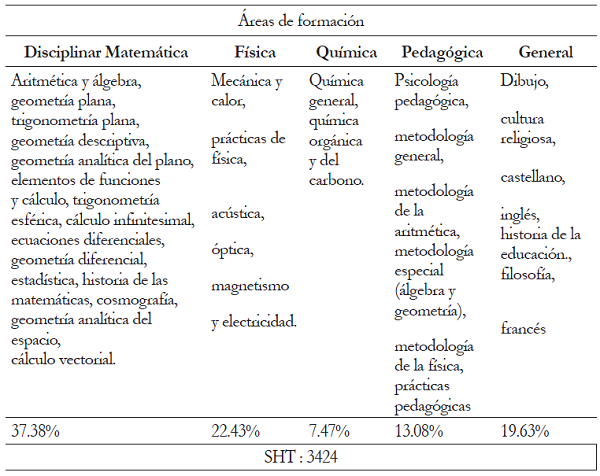
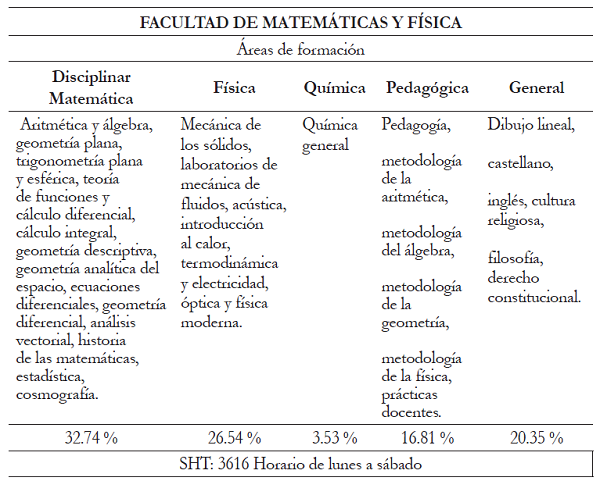
En el plan de estudios de 1957 (tabla 4) las áreas de formación en matemáticas y física se amplían de forma más detallada con algunos cursos como: estadística, cálculo diferencial, mecánica de sólidos, laboratorios, mecánica de fluidos, acústica e introducción al calor, termodinámica, electricidad, óptica y física moderna. En el área general surgen cursos como derecho constitucional y castellano, a pesar que desaparecen las prácticas de física y algunos cursos de matemática. El perfil profesional no varía.

Tabla 4

Plan de Estudios, año 195

Elaboración propiaTabla 4 El plan de 1957 perduró hasta 1961, cuando las facultades existentes desaparecen y se integran en la Facultad de Educación6, por la apertura de carreras técnicas en el área de ingeniería. En este plan, el área de formación matemática se amplía sustancialmente, aunque desaparece la estadística y la historia de las matemáticas. El porcentaje correspondiente al área disciplinar matemática pasa de 32.74% a 44.71%, lo cual evidencia la fortaleza que se le da al área, con nuevos cursos como lógica matemática, álgebra moderna, teoría de clases, topología general, geometría algebraica y topología algebraica. Por primera vez se evidencia la influencia de la llegada al país del Movimiento de la Matemática Moderna [MMM]. Son abolidas las metodologías específicas de la aritmética, de la geometría y de la física, disminuyendo así sustancialmente el área pedagógica (tabla 5).

Tabla 5

Plan de Estudios, año 1961.

Elaboración propia.Tabla 5 El Plan de 1965 evidencia que se pretendió formar docentes, también para la educación superior, por el fuerte componente disciplinar. El área disciplinar matemática se fortalece y abarca hasta el cálculo avanzado, la lógica matemática, el álgebra lineal I y II, las ecuaciones diferenciales parciales I y II, y la variable real I y II. Sin embargo desaparecen definitivamente asignaturas básicas como álgebra, geometría plana y del espacio, trigonometría plana y esférica, geometría proyectiva y geometría descriptiva, como consecuencia del MMM. Lo anterior evidencia también que empieza a formarse más un matemático que un profesor de matemáticas para educación básica y media, lo que se percibe en la fuerte formación disciplinar matemática, al pasar esta de 44.71% al 50.54% (tabla 6). En este plan la disminución en el área de física es dramática, al pasar del 27.64% al 5.49 %. Hay un incremento significativo en asignaturas del área profesional docente, con la realización de cuatro prácticas, a pesar que porcentualmente el área tiene menos peso. En el área general desaparecen dibujo, ética e historia de la filosofía, pero surgen materias como cultura física I y II, castellano I y II, humanidades I-IV, cuatro niveles de inglés básico y los niveles avanzados V y VI. En este plan el aumento porcentual al área general es bastante significativo y algo que llama la atención es que vuelven a aparecer varios niveles de cultura religiosa.

Tabla 6

Plan de Estudios, año 1965

Elaboración propiaTabla 6 De manera explícita se quiere formar docentes para la educación superior, con un fuerte componente matemático, con cursos complementarios de la Escuela de Graduados, que son específicos en el área disciplinar matemática. No se encuentran evidencias de por cuánto tiempo se desarrollaron esos estudios de la Escuela de Graduados.

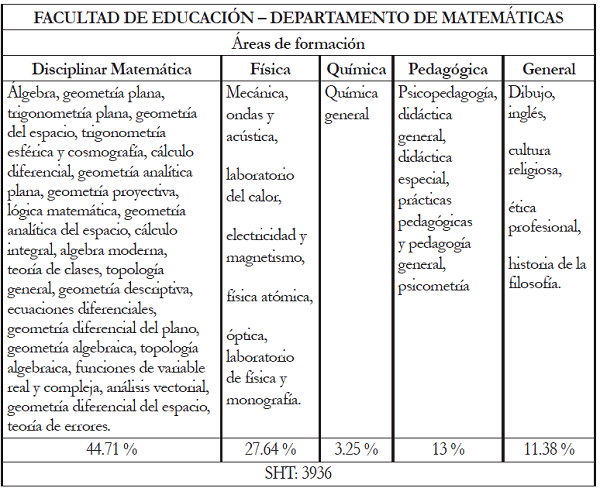
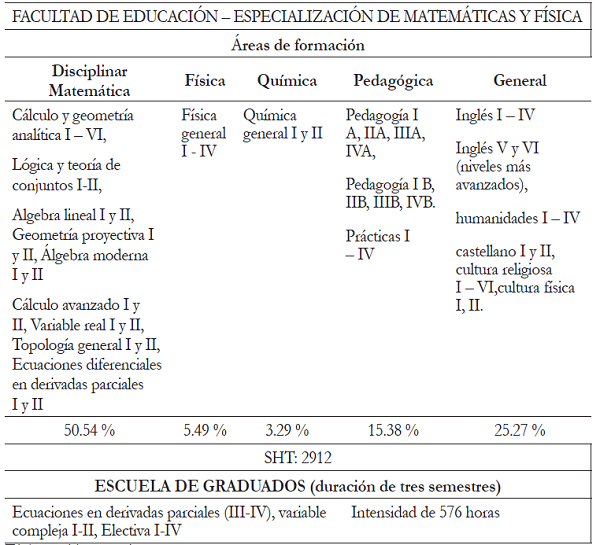
El plan anterior, con muy pequeñas variantes, permanece hasta uno nuevo en 1977. En este vuelven a aparecer la historia de las matemáticas y la física, aunque mantiene en esencia el plan de estudios anterior. En áreas como química, física y pedagogía, la formación se amplía, con asignaturas como química inorgánica, física moderna y sociología. Sin embargo las pedagogías IA al IVA y IB al IVB se sustituyen con nombres de asignaturas como: sociología educativa, consejería escolar, psicología general y evolutiva, metodología general, metodología especial y microenseñanza, ayudas educativas y evaluación del rendimiento escolar (tabla 7). Por primera vez aparece un seminario, como parte de la fundamentación investigativa. El perfil continúa siendo para profesionales en educación media, pero con un fuerte componente matemático y la posibilidad de ejercer en la educación superior. Al comparar el plan de 1977 con el de 1965, no se hace explícito el programa de Escuela de Graduados, el cual desapareció. Sin embargo, las asignaturas correspondientes se incorporaron al plan de estudios de la licenciatura. Lo anterior ratifica el fuerte enfoque de formación de profesores para el nivel superior, o en todo caso, la formación de un matemático. Desde este plan de estudios se expide el título de licenciado en matemáticas y física. El listado de cursos del área pedagógica deja ver que se implementó el enfoque de la tecnología educativa, dentro del llamado paradigma de la racionalidad técnica, con la aparición de las llamadas ciencias de la educación, fruto de un pretendido cientificismo en educación (Pérez & Velázquez, 1985).

Tabla 7

Plan de Estudios, año 1977

Elaboración propia.Tabla 7 Un nuevo plan de estudios es el de 1984, que en general tiene muy pocas variantes en comparación con el de 1977. La fundamentación disciplinar matemática continúa fuerte. Se busca un profesional que tenga buenas bases, no solo en matemáticas, sino en todas las áreas de formación.

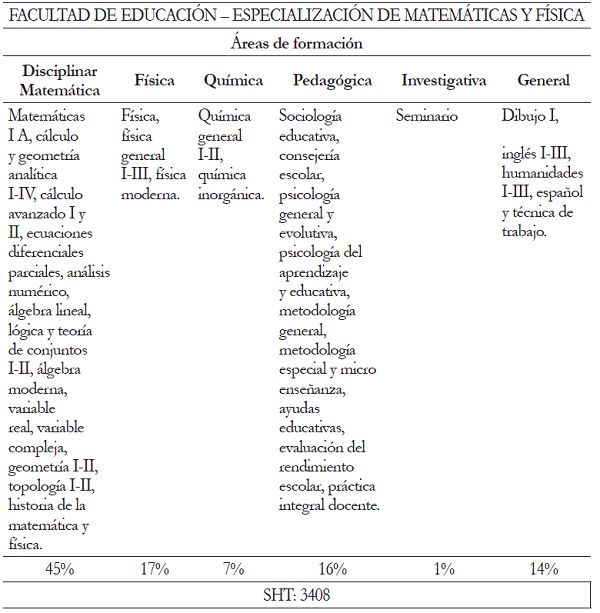
En el plan de estudios de 1991 hay pocas novedades, continúa una densa formación disciplinar matemática. Algunos cursos cambian de nombre. Se incluye por primera vez un curso de epistemología de la matemática, lo que refuerza la formación investigativa y se introducen cursos de computadores y ética profesional.

Es de destacar que con la nueva Constitución Política de 1991 se contempla la educación como un derecho y una obligación del Estado. Tres años más tarde se expide la Ley 115 de 1994 que define y regula la educación básica y media. En la formación de profesores establece que los programas deben

Formar un educador de la más alta calidad científica y ética; desarrollar la teoría y la práctica pedagógica como parte fundamental del saber del educador; fortalecer la investigación en el campo pedagógico y en el saber específico; y, preparar educadores a nivel de pregrado y de posgrado para los diferentes niveles y formas de prestación del servicio educativo. (Colombia, 1994)

En 1997 el MEN expide el Decreto 709 que regula la formación de profesores. Fija criterios para su mejoramiento profesional a través de la fundamentación de la teoría y la práctica pedagógica como eje del saber profesional del maestro y la práctica de la investigación formativa. El decreto exige cumplir unos estándares de calidad y para esto, los programas de formación deben entrar en un proceso de acreditación previa. Un año después, el MEN expide el Decreto 272 (1998), que concreta aspectos de la norma anterior y fija una nueva nomenclatura de títulos. Reorganiza las áreas de estudio del currículo, integra física, química y biología en una sola área denominada Ciencias Naturales. Así, las licenciaturas de física, química y biología desaparecieron en la UPTC. Según Guacaneme, Obando, Garzón y Villa (2013), esta norma modifica el énfasis de formación de la matemática por la educación matemática. Esta misma norma crea las licenciaturas en educación básica con énfasis en matemáticas, pero haciendo uso de la autonomía universitaria, la licenciatura de la UPTC solo reduce su nombre a Licenciatura en Matemáticas y mantiene en gran medida su estructura. Aunque no se hace explícito, este nuevo énfasis parece ser influenciado por los trabajos de Shulman (1986, 1987).

Un nuevo plan de estudios de la licenciatura es el del año 2000. Tiene la particularidad que todas las asignaturas cambian de nombre, al no referirse a los tradicionales, como cálculo, álgebra, entre otros. Esto fue una consecuencia del enfoque sistémico propuesto por el MEN para la enseñanza de las matemáticas (Decreto 1419, 1978), con una introducción tardía. Se integran cuatro bloques de asignaturas relacionadas entre sí, de la siguiente forma: sistemas básicos —con los cursos sistemas numéricos de naturales, racionales, reales y complejos; lógica matemática, teoría de conjuntos, geometría plana y del espacio, geometría analítica plana, y geometría vectorial—; matemáticas instrumentales —la matemática como herramienta: cálculo en una y varias variables, sucesiones y series, transformadas, ecuaciones diferenciales ordinarias y parciales y estadísticas descriptiva e inferencial—; estructuras básicas —estructuras algebraicas, categorías, dos topologías y tres de estructuras analíticas—; y tópicos de profundización electivos. El área pedagógica y profesional docente aparece con una estructura, ya no de asignaturas, sino de proyectos pedagógicos. Estos proyectos permitirían llevar a los estudiantes al contacto directo con el aula de clase y la escuela desde el primer semestre y no solo en la etapa final de prácticas. Otra cosa para destacar es la inclusión de tres didácticas específicas, a diferencia del plan anterior que solo contemplaba una. Este plan contempla un significativo aumento de la intensidad horaria en el área pedagógica al pasar del 25% al 40.1% del plan de estudios. Esto fue posible por la extensión de la duración de las licenciaturas de cuatro a cinco años, alcanzando una intensidad horaria total en 1248 horas de estudio. De acuerdo con el Proyecto Académico Educativo de la Licenciatura [PAE] (1999), este plan de estudios promovía la investigación en matemáticas y didáctica de la matemática. El perfil profesional era para desempeñarse en instituciones educativas de nivel básico y medio. En este plan, la formación en física se desvirtuó un poco y se denominó matemáticas aplicadas y comprendía cuatro asignaturas, las cuales podían ser cursadas en carreras como Física, Química, Biología, Ingeniería o Economía. Este plan fortalece la fundamentación investigativa, con epistemología, metodología de la investigación, y seminarios de investigación I y II. Por cada semestre se estableció un eje temático, el cual permitiría la transversalidad curricular, así: 1° semestre, el hombre; 2° semestre, la comunicación; 3° semestre, la pedagogía; 4° semestre, la didáctica; 5° semestre, la evaluación; 6° semestre, matemática en preescolar; 7° semestre, matemática en la básica; 8° semestre, matemática en la media. En este plan de estudios se hace evidente un componente ya más consistente sobre el conocimiento didáctico del contenido (Shulman, 1986).

Principios pedagógicos del trabajo docente.

A pesar de que los planes de estudio del programa contemplan el componente pedagógico, para los docentes del área disciplinar matemática no parece que eso tuviera trascendencia. Según las entrevistas, se infiere que para los profesores ese componente pedagógico es más o menos un grupo de cursos de relleno y casi innecesarios. Ratifican que lo importante es tener un buen dominio del contenido disciplinar matemático: “a enseñar se aprende en la práctica, _[…] ¿para qué perder tiempo con esos cursos de didáctica?” (E17, entrevista). La respuesta anterior es más o menos frecuente entre los matemáticos, para quienes lo que se necesita para enseñar matemáticas es saber la matemática. Según esto, se evidencia “una fuerte articulación entre las experiencias escolares de su formación y las formas de ejercer el trabajo docente” (Gonçalves & Wikboldt, 2016, p. 946), ya que los tres entrevistados eran licenciados. Cuando se les pide que en sus palabras expliquen “qué entienden por enseñar y por aprender matemáticas”, uno de ellos dice: “Para mí enseñar es explicar bien los contenidos en el tablero; y aprender, la verdad, pregúntele a los estudiantes” (E2, entrevista). Otro entrevistado responde: “Mi preocupación es la de enseñar. Ahora, aprender debe ser preocupación del estudiante” (E1, entrevista). Se ve aquí la influencia de los matemáticos y la falta de diálogo entre los profesores de las diversas áreas del programa, que es lo que armoniza un proyecto pedagógico de formación (Jiménez, Díaz & Leguizamón, 2010). A juzgar por lo declarado por profesores del área disciplinar, cada profesor solo está centrado en el desarrollo de su curso, desde la exposición centrada en el profesor, asumiendo las características de un modelo pedagógico tradicional (Leguizamón, 2017). Estos son aspectos centrales de cualquier plan de mejoramiento de programas que formación de profesores. El tercer entrevistado, profesor de una época más reciente, ya reconoce la importancia de la didáctica, la educación matemática y los cursos del área general. Afirma: “Sí claro. Es bueno que se conozca la didáctica y tenerla en cuenta, porque para los niños no es tan fácil como para nosotros comprender los conceptos” (E3, entrevista). A pesar de su afirmación, es claro que la didáctica se requiere en los niveles inferiores, pero no en el de la universidad.

Una de las tareas a futuro, y que aquí queda como posibilidad abierta de investigación, es repensar aspectos centrales de la formación de los futuros profesores, revisando la forma como se aprende, pues como proponen varios autores (Espinosa & Jiménez, 2014; Llinares, 2008; Riscanevo & Jiménez, 2017a), el diseño de entornos para aprender a enseñar matemáticas implica asumir que aprender a enseñar matemáticas es un asunto de participación en procesos sociales de construcción de conocimiento. Llinares (2008, p. 9) destaca que se debe analizar “la naturaleza de los entornos de aprendizaje en los programas de formación (las formas en las que los estudiantes para profesor y los profesores formadores interactúan)”, ya que estas definen una cultura y un contexto específico de aprendizaje.

De otro lado, se percibe que en la formación de profesores, y en el caso estudiado, se debe asumir que aprender debe ser tomado desde la práctica social para dar posibilidades que el estudiante viva una verdadera experiencia de aprendizaje y la convierta en algo valioso para él (Riscanevo & Jiménez, 2017b). Este es un núcleo de estudio abierto a investigaciones futuras sobre la formación de profesores de matemáticas.

Conclusiones

El Programa de Licenciatura en Matemáticas de la UPTC nace dentro de Curso Suplementario de Especialización Legalizada en 1928, como una sección de la Escuela Normal Superior de Tunja, para formar profesores de matemáticas. El plan de estudios del programa comienza con asignaturas que servirían de apoyo directo al desempeño en la educación media. Hacia 1954 aparece por primera vez en el plan de estudios la estadística y hacia 1957 el cálculo diferencial e integral. En el plan de estudios de 1961 el área de formación disciplinar se fortalece con todos los cursos de las diversas ramas de la matemática moderna. Para la misma época, en el área de formación pedagógica se introducen asignaturas como psicopedagogía, didáctica general, didáctica especial y psicometría; pero son abolidas las metodologías específicas de la aritmética, de la geometría y de la física. Con la introducción de estas asignaturas, se hace evidente la influencia del movimiento de la tecnología educativa o racionalidad técnica, llevado a la educación. Este plan de 1961 evidencia que se pretendió formar docentes, ya no solo para la educación básica y media, sino también para la educación superior.

Hacia 1965, el área disciplinar matemática se fortalece aún más, yendo hasta el cálculo avanzado, y a asignaturas como álgebra lineal I y II, ecuaciones diferenciales parciales I y II, y variable real I y II, lo que evidencia que empieza a formarse más un matemático que profesor de matemáticas para básica y media, como influencia de la entrada del MMM. Durante mucho tiempo el currículo no sufrió variaciones significativas y persistió un fuerte componente disciplinar. Hacia el año 2000, el área pedagógica aparece con una estructura, ya no de asignaturas, sino de proyectos pedagógicos, llamados así por la metodología de trabajo y el enfoque de relación más directa con la práctica escolar concreta en los planteles de educación básica y media, consecuencia también de nuevas normas (MEN, Decreto 272 de 1998).

La separación y falta de diálogo entre los profesores de las diversas áreas es un problema a superar en la licenciatura, pues como dice Tardif (2013, p. 39) al referirse a la formación de los profesores,

se trata de un ámbito que sigue estando subdividido en disciplinas y teorías múltiples que nunca lograron unificarse alrededor de una visión común del conocimiento profesional específico de los docentes. Esa es la razón por la cual, según diversas corrientes de investigación, los conocimientos de los docentes pueden corresponder a representaciones mentales, a creencias personales, a reglas tácitas de acción, a argumentos prácticos, a competencias, a saberes de acción.

Según el mismo autor, los conocimientos de los docentes no son una suma de “saberes o de competencias” que uno pudiera describir y encerrar en un libro o un catálogo de competencias. Se trata de saberes diversos e integrados a las prácticas docentes cotidianas, que están ampliamente condicionadas por costumbres, concepciones, intereses normativos, y políticos.

En la década de noventa se observa una cierta evolución en los métodos utilizados por los profesores, y comienza a cambiar la concepción que enseñar es sinónimo de exponer los contenidos temáticos en el tablero; el profesor es ya más consciente que debe preocuparse porque el estudiante aprenda. En la segunda parte de la investigación se presentarán los resultados del análisis de los últimos diecisiete años, junto con posibles respuestas a la investigación planteada al final del ítem anterior.

Referencias

Ball, D., Thames, M. & Phelps, G. (2008). Content Knowledge for Teaching: What makes it special? Journal of Teacher Education, 59(1), 389-407. https://doi.org/10.1177/0022487108324554

Carrillo, J. (2014). El conocimiento de los estudiantes para maestro desde la perspectiva de su especialización. En M. González, M. Codes, D. Arnau, & T. Ortega (eds.), Investigación en Educación Matemática XVIII (pp. 115-123). Salamanca: SIEM.

Cavalcante, P. & David, M. (2007). A formação matemática do professor: Licenciatura e prática docente escolar. Coleção Tendências em Educação Matemática. Belo Horizonte: Autêntica Editora.

Colombia. (1978). Decreto 1419. Ministerio de Educación Nacional. Bogotá, Colombia.

Colombia. (1994). Ley General de Educación. Ley 115. Ministerio de Educación Nacional. Bogotá, Colombia.

Colombia. (1997). Decreto 709. Ministerio de Educación Nacional.

Colombia. (1998). Decreto 272. Ministerio de Educación Nacional. Bogotá, Colombia: MEN.

Corbetta, P. (2007). Metodología y técnicas de investigación social. Bologna: McGraw Hill.

Decreto 2655 (1953). Por el cual se crea la Universidad Pedagógica y Tecnológica de Colombia con sede ene la ciudad de Tunja y se dicatan otras disposiciones. Universidad Pedagógica y Tecnológica de Colombia, Recuperado de https://virtual.uptc.edu.co/archivador/archivos/D2655-53.pdf

Escuela Normal Superior Santiago de Tunja. (s.f.) Archivo Histórico. Carpetas de resoluciones, decretos y certificados; 1917 – 1962. Tunja.

Espinosa, C., & Jiménez, A. (2014). Construcción del concepto de razón y razón constante desde la óptica socioepistemológica. Praxis & Saber, 5(9), 51-80. Recuperado de http://revistas.uptc.edu.co/index.php/praxis_saber/article/view/2993. https://doi.org/10.19053/22160159.2993

Fiorentini, D., & Creci, V. (enero-abril, 2017). Metassíntese de pesquisas sobre conhecimentos/saberes na formação continuada de professores que ensinam matemática. Zetetiké, 25(1), 164-185.

Gómez, Z. & Moreno, A. (2006). El currículo de la Licenciatura en Matemáticas de la UPTC (Monografía de grado, UPTC, Tunja, Colombia).

Guacaneme, E., Obando, G., Garzón, D., & Villa J. (2013). Informe sobre la formación inicial y continua de profesores de matemáticas: el caso de Colombia. Cuadernos de Investigación y Formación en Educación Matemática, 8, 1-49.

Jiménez, A. & Gutiérrez, A. (2017). Realidades escolares en las clases de matemáticas. Revista Educación Matemática, 29(2), 109-129.

Jiménez, A. (2010). La naturaleza de la matemática, las concepciones y su influencia en el salón de clase. Revista Educación y Ciencia, 13, 135-152. Disponible en: http://revistas.uptc.edu.co/index.php/educacion_y_ciencia/article/view/765/764

Jiménez, A., Díaz, M., & Leguizamón, J. (2011). Propuesta de modelo pedagógico para formar licenciados en matemáticas. Praxis & Saber, 2(3), 61-86. Recuperado de http://revistas.uptc.edu.co/index.php/praxis_saber/article/view/1110

Jiménez, A., Limas, L., & Alarcón, J. (2016). Prácticas pedagógicas matemáticas de profesores de una institución educativa de enseñanza básica y media. Praxis & Saber, 7(13), 127-152. Disponible en http://revistas.uptc.edu.co/index.php/praxis_saber/issue/view/377. https://doi.org/10.19053/22160159.4169

Jiménez, A., Suárez, N., & Galindo, S. (2010). La comunicación: eje en la clase de matemáticas. Praxis & Saber, 1(2), 175-189. Recuperado de http://revistas.uptc.edu.co/index.php/praxis_saber/article/view /1104/1103

Leguizamón, J. (2017). Patrones de interacción comunicativa del profesor universitario de matemáticas. Un estudio de caso. Praxis & Saber, 8(16), 57-82. Doi: http://dx.doi.org/10.19053/22160159.v7.n15.2016.572

Licenciatura en Matemáticas, Universidad Pedagógica y Tecnológica de Colombia. (1999). Proyecto Académico Educativo (PAE). Tunja.

Llinares, S. (25 de abril, 2008). Aprendizaje del estudiante para profesor de matemáticas y el papel de los nuevos instrumentos de comunicación. Conferencia invitada en el III Encuentro de Programas de Formación Inicial de Profesores de Matemáticas. Universidad Pedagógica Nacional, Bogotá, Colombia.

Martínez, J. (1988). El estudio de casos en la investigación educativa. Revista Investigación en la escuela,6. 41-49. Recuperado de https://idus.us.es/xmlui/handle/11441/59162

Pachón, L., Parada, R. & Chaparro, A. (2016). El razonamiento como eje transversal en la construcción del pensamiento lógico. Praxis & Saber, 7(14), 219-243. Disponible en: http://revistas.uptc.edu.co/index.php/praxis_saber/article/view/5224/4296. https://doi.org/10.19053/22160159.5224

Parra, L. (2003). La Universidad Pedagógica de Colombia y la Formación de Maestros 1953-1960. Tunja: Publicaciones de Magíster en Historia.

Pérez, R., & Velázquez, D. (1985). Dirección de Escuela de Matemáticas y Estadística: Documento de Evaluación de la Escuela de Matemáticas y Estadística, UPTC. Tunja: UPTC.

Ponte, J. (2001). A investigação sobre o professor de matemática: problemas e perspectivas do professor. Educação Matemática em Revista, 8(11), 10-33.

Riscanevo, L., & Jiménez, A. (2017a). La experiencia y el aprendizaje del profesor de matemáticas desde la perspectiva de la práctica social. Práxis & Saber, 8(18), 203-232. https://doi.org/10.19053/22160159.v8.n18.2017.7249

Riscanevo, L., & Jiménez, A. (2017b). El aprendizaje del profesor de matemáticas como campo investigativo. Revista Historia de la Educación Latinoamericana, 19(28), 173-196. https://doi.org/10.19053/01227238.6247

Rodríguez, O. (2004). El arte de recrear el pasado: historia oral y vejez productiva (Trad. R. Sánchez). Revista Historia de la Educación Latinoamericana, (6), 128-140. Recuperado de http://revistas.uptc.edu.co/index.php/historia_educacion_latinamerican/article

Santos, L. (1993). La naturaleza de las matemáticas y sus implicaciones didácticas. Mathesis,(9), 419-432. Recuperado de http://mathesis.digital/wp-content/uploads/2018/04/4.Santos.Naturaleza.Mat_.pdf

Schoenfeld, A. (enero-julio, 1998). Toward a theory of teaching-in-context. Issues in Education. Amsterdam, 4(1), 1-94. Recuperado de https://files.eric.ed.gov/fulltext/ED462374.pdf

Shulman, L. (1986). Those who understand: the knowledge growths in teaching. Educational Research15(2), 4-14.

Shulman, L. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57, 1-22.

Tardif, M. (2013). Las políticas de formación docente en América Latina. Avances y Desafíos Pendientes. En M. Poggi, Políticas docentes: formación, trabajo y desarrollo profesional (pp. 19-45). Buenos Aires: Unesco.

Notas