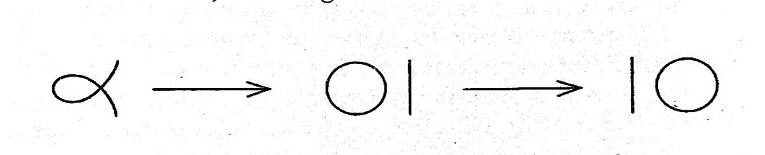Historical and epistemological perspectives of the number zero
Abstract
The historical and epistemological construction of the number zero is analyzed in this article as a theoretical basis for a research in the field of mathematical education, focused on categorizing the interpretations of students in initial math training about zero as a number. This analysis allowed the identification of cultural contributions made by different civilizations, such as the interpretation as a reference value in Egypt, its positional value in Mesopotamia, its use as a digit and as a number in India, among others. Furthermore, it was identified that the difficulties in its understanding have persisted, regardless of the context, to the point that these transcend and permeate its teaching. Consequently, a conceptual basis was established and founded that assumes the acknowledgement of history as a pedagogical value in the teaching of mathematics and that understands its relation with beliefs and perceptions about mathematics, which is articulated with the training of teachers as a research field.
Keywords: history of mathematics, epistemology, arithmetic, zero
Perspectivas históricas e epistemológicas do número zero
Resumo
Este artigo analisa a construção histórica e epistemológica do número zero como fundamento teórico de uma pesquisa no campo da educação matemática, focada em categorizar as interpretações dos estudantes na formação inicial de matemáticas sobre o zero como número. Esta análise permitiu identificar contribuições culturais feitas por diferentes civilizações, entre as quais destacam-se a interpretação como valor de referência no Egito, seu valor posicional na Mesopotâmia, seu uso como cifra e como um número na Índia, entre outros. Além disso, identificou-se que as dificuldades em sua compreensão têm perdurado, sem importar o contexto, ao ponto que transcendem e permeiam seu ensino. Consequentemente, foi estabelecida uma base conceitual que assume o reconhecimento da história como um valor pedagógico no ensino das matemáticas e que entende sua relação com as crenças e percepções da matemática, o qual se articula com a formação de professores como um campo de pesquisa.
Palavras-chave: história da matemática, epistemologia, aritmética, zero
Introducción
El número cero es considerado por muchos como la gema más preciada de las matemáticas, o en palabras de Aczel (2016) “el mayor logro intelectual de la mente humana” (p. 201). Su origen es todo un enigma y da cabida a una historia llena de secretos y muchas preguntas, que han llamado la atención de matemáticos, historiadores, arqueólogos, docentes investigadores, entre otros. Para comprender el papel del cero en las matemáticas, es necesario contextualizarlo en el surgimiento de esta disciplina, el cual no es definido con exactitud. Sin embargo, a través de los avances investigativos, se han encontrado convergencias particulares.
Se pueden tomar como punto de inicio las concepciones primitivas del hombre neandertal, que usó métodos arcaicos para enumerar y llevar cuentas. La evolución de tales métodos nos lleva al estudio de las matemáticas producidas por las civilizaciones antiguas, ya que “todos los pueblos civilizados, en el transcurso de su historia han dirigido sus esfuerzos hacia el estudio de las matemáticas” (Bell, 2004, p. 13). Particularmente, se tuvieron en cuenta las civilizaciones de Egipto, Mesopotamia, India, China, los mayas y los incas, y los aportes que realizaron a las ciencias, particularmente a las matemáticas. Cada civilización logró significados diversos del número cero. Algunas lo usaron como valor de referencia o marcador de posición y otras como número, muchas veces ligado a la representación numérica de la nada (Barrow, 2012).
En la diversidad y contextualización de estos significados, la educación matemática como campo investigativo ha señalado que el cero como número genera grandes preocupaciones en su enseñanza y aprendizaje, pues, en palabras de D’Amore y Fandiño (2012), “el cero constituye un obstáculo epistemológico, […] basta ver su controvertida, larga y tormentosa historia” (p. 101). Para comprender la complejidad del número cero, es necesario hacer una rigurosa revisión bibliográfica sobre este misterioso y enigmático número.
Surgimiento de los números
La matemática ha estado presente en la vida del hombre desde tiempos inmemoriales. Aunque no es posible determinar su origen con claridad, los primeros registros que se conocen datan del 35 000 al 20 000 a. C. y están relacionados con problemas primitivos de conteo (Burton, 2011; Gutiérrez, 2009). Para comprender su inicio, arqueólogos, paleontólogos e historiadores han reconstruido los sucesos de nuestro pasado prehistórico con base en fragmentos de piedras y huesos conservados en las entrañas de la tierra, y descubiertos por la curiosidad del hombre y la necesidad de conocer su pasado (Mankiewicz, 2005; Seife, 2006).
Uno de los registros más antiguos hasta ahora descubiertos es el hueso de un babuino con 29 muescas —35 000 a. C.— y fue encontrado en África. Aproximadamente de la misma fecha, en la República Checa se encontró el hueso de un lobo con 55 muescas, divididas en dos grupos, uno de 30 y el otro de 25 (Barrow, 2012; Ifrah, 1987; Mankiewicz, 2005). El hueso de Ishango —20 000 a. C.— (figura 1), registro de gran importancia en la historia de las matemáticas, fue encontrado en la ribera del lago Edward en África Central.

Figura 1. Hueso de Ishango. Tomada de Burton (2011, p. 5).
Se cree que estos registros están relacionados con el conteo de una colección de objetos, posiblemente de los animales que cazaban, o para medir el paso del tiempo, lo que coincidiría con las fases lunares o el calendario menstrual de la mujer (Burton, 2011; González, Martín & Silván, 2010; Mankiewicz, 2005). De esta manera se evidencian las primeras nociones del hombre primitivo sobre los números, relacionadas con algunos de sus usos: contar y medir (Gómez, 1993).
Las necesidades de conteo cada vez más exigentes llevaron a la sofisticación de los métodos para contar y, en consecuencia, a la evolución de los primeros sistemas numéricos, considerados el primer lenguaje escrito del hombre, anterior a la escritura y las letras (Dantzig, 1971; Ifrah, 1987; Seife, 2006).
Los registros más antiguos sobre los primeros sistemas numéricos datan del 3500 a. C. y se les atribuyen a las civilizaciones de los egipcios y babilónicos (Dantzig, 1971). Por un lado, en las riberas del río Nilo se establece la civilización egipcia y, del otro, entre los ríos Tigris y Éufrates, la civilización babilonia. Estas son dos de las primeras civilizaciones que son un buen referente como punto de partida de las matemáticas en la vida del hombre en sociedad, pues en ellas hay uso de grafos para registrar el paso del tiempo, llevar un control de los alimentos y posiblemente realizar trueques, actividades del hombre primitivo en las que no era necesario concebir la nada o la falta de objetos como cantidad, pero que evidencian la invención de los primeros sistemas numéricos.
Primeros indicios del cero
Egipto se considera una de las primeras civilizaciones en poseer registros escritos sobre el uso de los números. Desarrollaron un sistema numérico con siete símbolos para representar los números 1, 10, 100, 1000, 10 000, 100 000 y 1 000 000 (figura 2). La manera de usarlos se basaba en un sistema aditivo en base 10, el cual les permitía repetir cada símbolo hasta nueve veces (Ríbnikov, 1987; Stewart, 2012).
En el sistema numérico desarrollado por los egipcios no era necesario un símbolo para representar una casilla vacía o expresar la ausencia de objetos. Sin embargo, Lumpkin (2004) y Joseph (2008) comentan que alrededor de 1770 a. C., en el Imperio Medio de esta civilización, que corresponde a la dinastía XIII, surge el cero por primera vez en la vida del hombre interpretado de dos modos diferentes: como valor de referencia era usado en los planos de las construcciones para referirse al nivel de la base; y para denotar equilibrio en los estados de cuentas mensuales. Su símbolo fue el jeroglífico nfr (figura 3) y se encontró en el papiro Boulaq 18.

Figura 2. Representación simbólica de numeración egipcia. Adaptada de Stewart (2012, p. 16).
La civilización babilónica, a mediados del 3000 a. C., desarrolló un sistema numérico posicional en base 60 que, a diferencia de los egipcios, favoreció el registro de grandes cantidades con un número menor de símbolos. Así podían llevar un mejor control de sus bienes o de los intercambios comerciales (Ifrah, 1987; Sen & Agarwal, 2015). Gracias al uso de estiletes y arcilla para escribir, hoy en día se conservan muchos registros de sus avances (Collette, 1991), lo que permite realizar un estudio más preciso del surgimiento del cero como marcador de posición.

Figura 3. El papiro Boulaq. Tomado de Jaramago (2008).
Kaplan (2004) menciona que a mediados del 2000 a. C. los babilonios usaban dos símbolos para escribir números. Para el uno usaban:  ; y para el diez,
; y para el diez,  . Por ejemplo, para representar el 13, usaban
. Por ejemplo, para representar el 13, usaban  ; para el 59,
; para el 59, 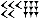 . Para representar el 60, como coincide con la base del sistema, usaban el mismo símbolo del uno. Así, en el caso del número 63, en ocasiones lo escribían:
. Para representar el 60, como coincide con la base del sistema, usaban el mismo símbolo del uno. Así, en el caso del número 63, en ocasiones lo escribían:  , en el que aumentaban el tamaño del uno que representaba 60 para diferenciarlo de los demás símbolos. En ocasiones, dependiendo del escriba, dejaban un espacio separándolo de los demás:
, en el que aumentaban el tamaño del uno que representaba 60 para diferenciarlo de los demás símbolos. En ocasiones, dependiendo del escriba, dejaban un espacio separándolo de los demás:  .
.
Esto muchas veces generaba ambigüedades y, para poder interpretar la cantidad que se representaba, era necesario tener en cuenta el contexto en el que se escribían los datos (Burton, 2011; Kaplan 2004; Seife, 2006). El problema se complicaba aún más cuando era necesario dejar una casilla vacía, como es el caso de la representación de 3610 (figura 4), pues se usaban los mismos símbolos que para escribir 610.
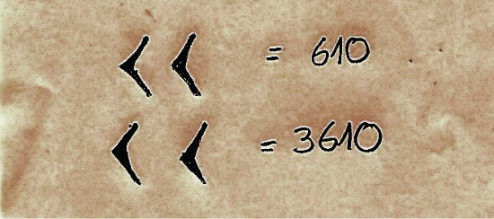
Figura 4. Representación numérica babilónica. Elaboración propia.
Para evitar los problemas de interpretación y las ambigüedades, surge la necesidad de un marcador que permita reconocer cuando hay una casilla vacía. Como lo afirma Burton (2011), “solo en un sistema posicional se debe especificar la existencia de un espacio vacío, problema que no tuvieron los egipcios” (p. 25). En consecuencia, en 300 a. C., los babilonios usaban dos cuñas inclinadas para representar una posición en blanco o vacía, lo que permitía observar con claridad la posición que tenían los símbolos al ocupar una cifra determinada de un número (Seife, 2006).
Siguiendo con el ejemplo de la representación de 3610, se observa en la figura 5 el uso del nuevo marcador de posición. Al respecto, Ifrah (1987) afirma: “el doble clavo oblicuo de los sabios mesopotámicos fue comprendido en el sentido de vacío” (p. 231). Así surge una de las interpretaciones que se le da al cero, marcador de posición de una casilla vacía, aunque no se consideró como número (Stewart, 2016).
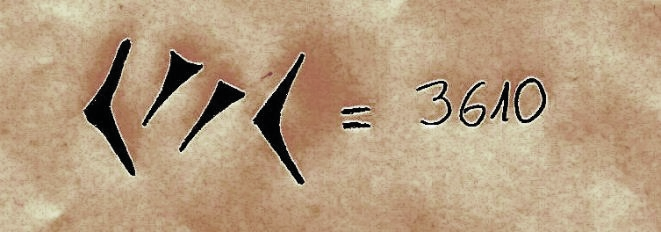
Figura 5. Representación simbólica en el sistema babilónico del número 3610. Elaboración propia.
Sobre las matemáticas desarrolladas en Egipto y Mesopotamia, cabe destacar la evolución que lograron del pensamiento matemático y la comprensión de los sistemas numéricos, ya que dieron el importante paso de lo concreto a lo abstracto, al comprender que tres manzanas, tres vacas y tres espigas representaban la misma cantidad (Aczel, 2016). Así la concepción de número es dotada de un sentido abstracto, muy importante para comprender el cero como número.
Otra de las civilizaciones del Antiguo Oriente que se destacó por sus avances en matemáticas y, en especial, sobre sistemas numéricos es China. En la dinastía de los Han —200 a. C.—, independientemente del trabajo realizado en Mesopotamia, desarrollaron un sistema numérico posicional en base 10, en el que usaban barras verticales y horizontales (Ifrah, 1987). Este fue el primer sistema numérico decimal en considerar nueve símbolos, en el que se rotaban las varillas para diferenciar las cifras contiguas (Barrow, 2012; Gómez, 2009; Katz, 2009). Las varillas ubicadas verticalmente (figura 6a) eran usadas para las unidades, centenas, decenas de mil. Al ubicarlas horizontalmente (figura 6b) representaban las decenas, unidades de mil, centenas de mil (Lam, 1988). A diferencia de la civilización babilónica, este método les permitía diferenciar cuándo existía una casilla vacía sin la necesidad de dejar un espacio o adicionar otro símbolo (figura 6c).

Figura 6. Numeración china de varillas. Adaptada de Barrow (2012, p. 41).
El cero es interpretado por la civilización china como la ausencia de elementos. Es de destacar que los chinos comprendieron el uso del cero, aunque no desarrollaron un símbolo para representarlo. Según Gómez (2009) e Ifrah (1987) no fue sino hasta mediados del siglo VIII d. C. cuando arribó el cero hindú, gracias a los intercambios comerciales con India y por influencia de astrónomos y matemáticos.
Otra de las primeras civilizaciones del mundo antiguo que creó un sistema numérico con la presencia del cero fue la civilización maya en Mesoamérica, en el periodo Preclásico Tardío —400 a. C.- 200 d. C.—. Este es considerado como un gran logro intelectual y uno de los más antiguos ejemplos del cero en el mundo (Sharer, 2003). El sistema numérico que desarrollaron era posicional en base 20 y lo escribían de manera vertical con la combinación de tres símbolos: un punto para el uno, la barra para el cinco y una concha  para el cero (Fedriani & Tenorio, 2004). Así, por ejemplo, para escribir el número 120 (figura 7), los mayas ubicaban un punto sobre una barra en el segundo nivel y una concha en el primer nivel.
para el cero (Fedriani & Tenorio, 2004). Así, por ejemplo, para escribir el número 120 (figura 7), los mayas ubicaban un punto sobre una barra en el segundo nivel y una concha en el primer nivel.

Figura 7. Representación numérica maya para el 120. Elaboración propia.
Además de la concha de caracol, que hacía alusión al ciclo del molusco que llegaba a su fin, los mayas usaron otros símbolos para representar el cero (figura 8), entre los que se destacan: la semilla de maíz, que simbolizaba el inicio y el fin del ciclo que cumple la semilla antes de llegar a la tierra y pasar al siguiente nivel; y la flor, que simboliza el paso de la categoría espiritual a lo material. Todas evocan completitud, de manera que para continuar o seguir al próximo nivel es necesario estar en paz o en plenitud (Duque, 2013).
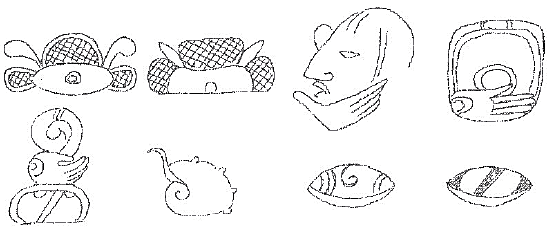
Figura 8. Algunos símbolos mayas para el cero. Tomado de Kaplan (2004, p. 82).
Los mayas interpretaron el cero como plenitud o estado completo, y aunque no era considerado como número, se dotó de un sentido especial que permitía al sistema numérico ser operativo (Duque, 2013).
Continuando con las civilizaciones en América, cabe resaltar las concepciones numéricas desarrolladas por los incas en Perú, que a falta de un método escrito para registrar cantidades, emplearon cuerdas de varios colores y diferentes nudos para llevar sus registros contables (figura 9). El quipu, como se conoce, era un método muy efectivo en el que no era necesario emplear símbolos elaborados para el registro de cantidades. Era usado exclusivamente por un oficial de nudos, llamado quipu-camayoc, quien era el encargado de registrar y conservar cualquier información contable (Burton, 2011; Fedriani & Tenorio, 2004; Schmidt & Santos, 2016).
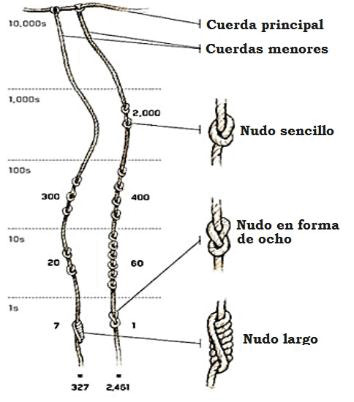
Figura 9. Interpretación de números en el quipu. Tomada de Pilgaonkar (2014, p. 4).
Estas representaciones se basaban en un sistema numérico decimal, en el que usaban tres tipos de nudos: un nudo sencillo, uno en forma de ocho y otro formado por varias vueltas. Cada uno simbolizaba una cantidad específica dependiendo de su ubicación. Además, Armengol (2010) afirma que “también había un símbolo para el cero: una cuerda sin nudos” (p. 177). De este modo era posible identificar cuándo había una posición vacía (figura 10) y se lograba representar la ausencia de unidades (Burton, 2011; Gutiérrez, 2009; Schmidt & Santos, 2016). Los incas, aunque no desarrollaron un lenguaje escrito para su sistema numérico, comprendieron la interpretación del cero como casilla vacía o ausencia de unidades.

Figura 10. Ejemplo de la interpretación numérica en el quipu. Tomada de Pilgaonkar (2014, p. 4).
Ninguna civilización antigua concibió el cero como número. Sin embargo, todas lograron desarrollar un símbolo para representar la ausencia de objetos, designar un valor de referencia o para denotar plenitud, algunas de las interpretaciones que se le atribuyen al cero como número.
El cero como número
El cero es considerado una de las grandes conquistas del intelecto humano, rodeado de misticismo, tropiezos y magnificencias (Seife, 2006). Para Stewart (2016) “antes del siglo IX d. C., el cero era visto como un símbolo práctico para los cálculos numéricos, pero no se le consideraba un número como tal; probablemente, porque no contaba nada” (p. 146). El cero, para ser considerado como un número, ha atravesado un camino largo de interpretaciones y atribución de significados. Ciro (2011) afirma que “pasó mucho tiempo, siglos y milenios para que nos diéramos cuenta de que los números se definen por sus propiedades, de ahí que el símbolo de un espacio vacío pasara a ser un número” (p. 31). Según Berlinghoff y Gouvêa (2010) y Nieder (2016) para considerar el cero como número es necesario desligarlo de la experiencia empírica y llevarlo al plano abstracto, con el fin de brindar las condiciones necesarias para definirlo como un objeto.
El origen del cero ha pasado de especulaciones a importantes investigaciones. Waerden (1988), en referencia a la teoría de Freudenthal sobre el origen del número cero, menciona que fue desarrollado por los hindúes gracias a la influencia de los astrónomos griegos y al sistema sexagesimal de los babilónicos —entre 200 d. C. y 600 d. C.—, aspecto que se evidencia en Sûrya Siddhânta, tratado hindú sobre astronomía en el que abundan términos griegos.
Por otra parte, en Diller (1996) y Divakaran (2018) se reconoce a George Cœdès como el historiador y arqueólogo francés que concluyó a partir de sus investigaciones que el origen del cero y su valor posicional están relacionados con inscripciones en sánscrito (figura 11) provenientes de Camboya, al sur de la península Indochina, las cuales relatan el inicio de la era Çaka en el año 605 d. C. (Cœdès, 1931).
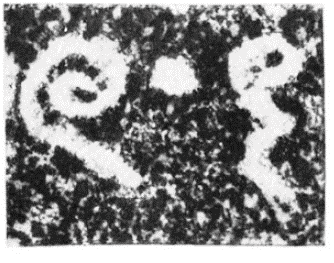
Figura 11. Inscription Khmère de Sambór. Tomada de Cœdès (1931, p. 326).
Según Aczel (2016), por muchos años el descubrimiento de Cœdès, conocido como Inscripción K-127, se consideró el primer registro del cero como número. Sin embargo, las investigaciones de la Biblioteca Bodleiana de la Universidad de Oxford sobre la datación del manuscrito Bakhshali proveniente de India, en que se registran varios ceros, lo ubican entre el 224 y 383 d. C. (Bodleian Libraries, 2017). Un ejemplar de su aparición se observa en la figura 12, correspondiente al folio 16.

Figura 12. MS Sansk. d.14 fol. 16v. Tomado de Bodleian Libraries (2017).
A mediados del siglo VI d. C, según Castillo (2011) y Gómez (1993), la genialidad de los hindúes y su pasión por los números los llevó a conformar el sistema numérico Kharosthi, un sistema numérico posicional en base diez. Este sistema evolucionó gradualmente hasta la numeración Brahmi (figura 13a), la cual estaba conformada por diferentes símbolos del 1 al 10 y potencias superiores, sin contar de momento con la presencia del cero (Gutiérrez, 2009; Mankiewicz, 2005). Al rededor del 876 d. C., estos numerales evolucionaron hasta conformar el sistema Gwalior (figura 13b). Algunos registros de este sistema se encontraron en un templo de la fortaleza hindú de la ciudad de Gwalior, al noroeste del estado de Madhya Pradesh. Estaba formado por diez símbolos en los que se incluía un óvalo que representaba el número cero, muy similar al usado actualmente (Castillo, 2011; Webb, 2015).
De acuerdo con Ifrah (1987), el sistema numérico hindú se destacó de los demás sistemas por dos grandes aspectos: estaba conformado por símbolos diferentes entre sí que no evocaban la cantidad que representaban; y, verbalmente, estaban dotados de un lenguaje con sentido posicional, ya que realizaba pequeñas variaciones según la posición que ocupaba cada número. Joseph (2008) resalta el papel multifacético del cero en este sistema, pues era usado como símbolo, número, magnitud, separador de dirección y marcador posicional, todo dentro de un sistema numérico posicional completamente establecido.

Figura 13. Sistemas de numeración hindú. Tomado de Castillo (2011, p. 29).
Los árabes que llegaron a la India se percataron de las grandes ventajas del sistema numérico hindú, se apropiaron de él y lo divulgaron en el mundo islámico. De esta forma nace el sistema numérico indo-arábigo, el cual “se puede colocar con todo merecimiento entre los mayores descubrimientos técnicos de la humanidad, junto con la invención de la rueda, el fuego y la agricultura” (Paulos, 1993, p. 181). El matemático árabe Al-Jwarizmi escribió uno de los primeros tratados en el que expone sus ventajas —Kitāb al-Jam ‘wa-l-tafrīq bi-hisāb al-Hind, que traduce: Libro para el cálculo con números hindú—. Al tratarse de un libro importante como referencia para el estudio de las matemáticas, es traducido al latín para ser divulgado por Europa, aunque su arribo fue lento y retrasado por concepciones religiosas, filosóficas y políticas, que truncaron el desarrollo de las ciencias en lo que se conoce como oscurantismo medieval (Asimov, 2000; Castillo, 2011).
Un símbolo para el cero
Para tratar el cero como número, era indispensable un símbolo que lo representara y a la vez lo diferenciara de los demás. De un lado, se cree que el símbolo 0 es originario de Grecia, posiblemente propuesto por el astrónomo Claudio Ptolomeo, que usó la primera letra —ómicron— de la palabra ουδεν, para referirse a la nada o, de una manera abstracta, al paso de algo a la nada (Betti, 2017). Este punto de vista tiene gran relación con la teoría de Freudenthal sobre el origen del número cero. Sin embargo, Kaplan (2004) refuta esta idea al afirmar que “Otto Neugebauer, la autoridad más importante en textos griegos sobre astronomía descarta de manera tajante toda esta explicación; […] los griegos ya habían asignado el valor numérico 70 a ómicron” (p. 37).
De otro lado, Subhash Kak (citado por Barrow 2012) propone que evolucionó del símbolo que era usado en Brahmi para el número 10, semejante a un pez, el cual se fue separando para dar lugar al uno y al cero (figura 14). Finalmente, Ifrah (1987) menciona que inicialmente se simbolizó con un punto —bindu—, que evolucionó hasta convertirse en un pequeño círculo —en sánscrito chidra, palabra para agujero—. Este último coincide con los primeros registros del cero expuestos por Cœdès (1931) y la Biblioteca Bodleiana de la Universidad de Oxford (2017).
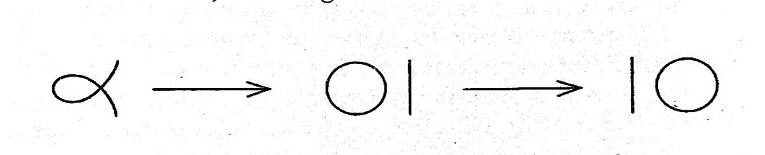
Figura 14. Posible separación del símbolo pisciforme para 10 en una línea para el 1 y un círculo para el 0. Tomada de Barrow (2012, p. 54).
Este símbolo —independientemente de la concepción de su origen— se ganó un lugar muy importante en el sistema numérico como un elemento más. Para referirse a él, entre los siglos VI y VIII, los sabios hindúes empiezan a usar la palabra śūnya, que significa vacío o ausencia de algo que puede ser llenado (Barrow, 2012; Betti, 2017; Ifrah, 1987). Producto de los intercambios comerciales liderados por los árabes y su deseo por recopilar y traducir los manuscritos que adquirían en sus conquistas por el viejo mundo, a mediados del siglo IX surge la palabra as-sifr —traducción árabe para śūnya—, la cual conservó su significado original (Barrow, 2012; Burton, 2011; Castillo, 2011; Joseph, 2008).
La evolución de la palabra as-sifr, que es el origen etimológico de la palabra cero, siguió su curso: en el siglo XIII es traducida al latín y dio origen a las palabras cifra y zefirum. La primera adoptó el significado amplio para referirse a cualquier símbolo numérico. La segunda mantuvo su significado y fue traducida al italiano en el siglo XIV. Se encuentra en varios escritos como zefiro, zephyr, zefro o zevero, que en el dialecto veneciano se abrevió como zero, palabra que es usada actualmente en el inglés y francés para indicar cuándo una potencia de diez no se tiene en cuenta al escribir los dígitos de un número (Barrow, 2012; Berlinghoff & Gouvêa, 2010; Pogliani, Randic & Trinajstić, 1998).
El cero y las operaciones básicas
Históricamente, operar con el número cero requiere de un cuidado especial en virtud de las propiedades particulares que lo diferencian de los demás números, que muchas veces lleva a evitar operarlo dada la complejidad en su comprensión (Joseph, 2008). Al respecto, Webb (2015) afirma que “la práctica de aritmética con el cero solía dar resultados extraños, a veces tanto que hubo que prohibirlos” (p. 149). Para comprender las propiedades aritméticas del cero, es necesario describir la génesis de su relación con los demás números.
Uno de los primeros registros del cero como número se encuentra en el manuscrito Bakhshali —siglo III d. C.—, que posiblemente fue escrito por cuatro o cinco escribas. En él se describen algunos problemas de aritmética, geometría y medición (Bodleian Libraries, 2017; Puttaswamy, 2012). Desde entonces, en los textos dedicados al estudio de las matemáticas, se incluían un capítulo para la aritmética —ganita o patiganita— y otro para el álgebra —aryakat-ganita o bijaganita—, en los que se desarrollaron procesos puramente algorítmicos, facultad que les permitió operar números muy grandes de manera fácil y efectiva (Betti, 2017; Joseph, 2008; Logan, 2017).
En el siglo VII, Brahmagupta fue el pionero en el estudio del cero y sus propiedades. Inicialmente lo definió como “el resultado de sustraer cualquier número de sí mismo” (Barrow, 2012, p. 53). En su obra Brahma-Sphuta-Siddhanta —El inicio del universo—, dedica un capítulo completo al estudio de problemas aritméticos y de progresiones aritméticas y geométricas (Joseph, 2008; Mankiewicz, 2005; Webb, 2015). En esta obra, Brahmagupta menciona tres términos importantes: los bienes —números positivos—, las deudas —números negativos— y la nada —número cero—. Ifrah (1987), al respecto, menciona:
El sabio descubría una de sus reglas fundamentales: una deuda deducida de la nada se transforma en un bien, y un bien deducido de la nada se transforma en una deuda (el número opuesto a un número positivo es un número negativo y a la inversa). (p. 277)
Además, en referencia al trabajo de Brahmagupta, Barrow (2012) indica que “cuando se añade sunya a un número o se sustrae de un número, el número permanece invariable; y un número multiplicado por sunya se convierte en sunya” (p. 53). Estas reglas, que Brahmagupta relacionó principalmente con la solución de expresiones algebraicas, están relacionadas de igual forma con los números positivos y negativos que abarcan tanto la aritmética como el álgebra (Divakaran, 2018).
Según Divakaran (2018), Brahmagupta logró definir con increíble exactitud las propiedades aritméticas del cero. Destaca la división, ya que definió 0/0 como 0, y cuando el numerador fuera distinto de cero, Brahmagupta afirmaba que se debía dejar como quedaba, ya que no era posible definirlo. Seife (2006), al respecto, menciona que “multiplicar por cero desploma la línea numérica. Pero dividir por cero destruye por completo el armazón de las matemáticas” (p. 31).
No transcurrió mucho tiempo, hasta que Bhāskarāchārya —conocido como Bhaskara II—, en su obra Siddhanta Siromani realizara un compendio completo sobre aritmética y álgebra basado en el trabajo de sus predecesores —Brahmagupta, Sridhara, Padmanabha y posiblemente Mahavira—, en el que retoma las operaciones con cero. Allí define la división por cero como infinito (Berlinghoff & Gouvêa, 2010; Divakaran, 2018).
En Castillo (2011) se encuentra la siguiente afirmación, que hace parte del capítulo “Bijaganitha”:
La fracción en la que el denominador es cero se llama cantidad infinita. En esta cantidad en la cual cero es el divisor no hay alteración posible por mucho que se añada o se quite, lo mismo que no hay cambio en Dios infinito e inmutable. (p. 84)
De acuerdo con Romig (1924), el matemático inglés John Wallis, a mediados del siglo XVII, afirmó que el cociente que resultaba de dividir por cero no era un número y usó ∞ para simbolizarlo.
Es de gran importancia destacar la genialidad de los hindúes y su gran aporte a las matemáticas. Llevaron los números de lo tangible a lo abstracto, paso crucial para el desarrollo de las matemáticas en el mundo, en el que juega un papel fundamental el número cero (Webb, 2015).
El recorrido histórico del cero por algunas civilizaciones, los significados, símbolos y nombres que le atribuyeron se observan en la figura 15, en la que se sintetizan algunas contribuciones para su interpretación en diferentes contextos.
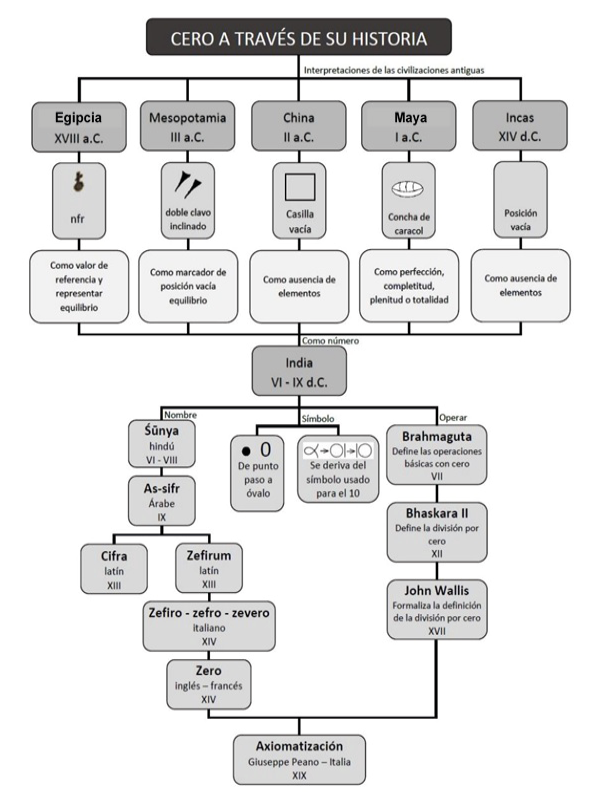
Figura 15. Interpretaciones y representaciones del cero desde su historia. Elaboración propia.
El cero llega de Oriente a Europa
La proliferación de las matemáticas de la India en Occidente inicia con los árabes, quienes llegan a la India —en principio de manera pacífica a través de los intercambios comerciales— con el ánimo de promover el islam y adquirir nuevas ideas (Castillo, 2011). Se presume que a mediados del siglo VIII el matemático árabe Al-Jwarizmi estudió la numeración hindú influenciado por la visita de eruditos hindúes a la corte del califa al-Ma’mūn en Bagdad, de los que logró aprender el avance en matemáticas y astronomía desarrollado en India. De sus estudios logró escribir su obra Kitāb al-Jam ‘wa-l-tafrīq bi-hisāb al-Hind —Libro para el cálculo con números hindú—, del que solo se conservan algunas traducciones (Berggren, 1986; Castillo, 2011).
De las apreciaciones de Al-Jwarizmi sobre la numeración hindú, Barrow (2012) resalta la siguiente:
Cuando [después de restar] no queda nada, ellos escriben el círculo pequeño, de manera que el lugar no queda vacío. El círculo pequeño tiene que ocupar la posición, porque de otra forma habría menos lugares, de modo que el segundo podría tomarse erróneamente como el primero. (p. 62)
De otro lado, el matemático árabe Kūshyār ibn Labbān, alrededor del siglo XI escribe U ṣūl ḥ isāb al - hind—Principios de la contabilidad hindú—, obra dedicada al estudio de la aritmética elemental basada en el sistema de numeración hindú, en el que aparece el cero como marcador de una posición vacía —as-sifr—. Esta obra adquirió gran importancia en el mundo islámico (Berggren, 1987; Vogel, 1966).
Aunque se podría suponer que la expansión árabe se llevó a cabo por la península balcánica, su paso a Europa se dio por el mar Mediterráneo hasta llegar a la península ibérica —concretamente a España—, de manera que el cero hindú, después de aparecer en Bagdad, pasó a Córdoba y de allí al resto de Europa (Barrow, 2012; Betti, 2017; Burton, 2011; Doval, 2005). Su divulgación en Europa estuvo a cargo de dos grandes matemáticos: el primero fue el francés Gerberto de Aurillac —945-1003—, quien tuvo la oportunidad de conocer el sistema numérico indo-arábigo y sus ventajas en uno de sus viajes por la península ibérica. Sus trabajos estuvieron enfocados a la geometría, astronomía y métodos de cálculo, en los cuales usaba una ficha de cuero llamada sipos para referirse al cero (Barrow, 2012; D’Amore & Fandiño, 2012).
El segundo fue Leonardo Pisano —1175-1240—, conocido bajo el seudónimo de Fibonacci, a quien se le atribuye el inicio del renacimiento matemático de Europa Occidental (Colerus, 1943). Gracias a la profesión de su padre como comerciante, Fibonacci viaja por varios países a través del mar Mediterráneo. Conoció el sistema numérico hindú, del cual no dudó en reconocer las ventajas que tenía sobre los demás sistemas numéricos (Burton, 2011). En su obra culmen, Liber Abaci —Libro de las cuentas—, realiza un estudio completo sobre la matemática del siglo XIII, con el fin de llevar a Italia las mejores matemáticas para su uso en general. Los temas del Liber Abaci son aritmética, álgebra y resolución de problemas, en los que emplea nociones geométricas euclidianas para realizar sus pruebas. En el primer capítulo expone las ventajas del sistema numérico, comprendido por nueve cifras y un marcador de posición, que él llamó zephyr (Burton, 2011, D’Amore & Fandiño, 2012; Sigler, 2012). Gracias a estos dos precursores, se da a conocer en Europa el sistema numérico hindú —o indo-arábigo—, y con este, el cero hindú. Su uso estandarizado fue posible gracias a la invención de la imprenta, de manera que los símbolos que se usan en la actualidad no han sufrido modificaciones considerables desde el siglo XV (Burton, 2011).
La aceptación del cero en Europa
Desde su salida de India, el panorama del cero era prolífero, sin embargo, su aceptación en Europa estaba condicionada por varios factores. Uno de ellos fue la influencia de la matemática de los griegos, la cual estaba regida por principios lógicos y geométricos, y era estudiada en gran parte del continente por comunidades religiosas, en las que prevalecían las ideas teológicas sobre el desarrollo de la ciencia, por lo que el cero proveniente de la matemática islámica no era bien aceptado por sus creencias religiosas (Barrow, 2012; Betti, 2017; Joseph, 2008).
Seife (2006) y Webb (2015) mencionan que el cero estaba enmarañado por las concepciones peligrosas sobre el ser y no ser, el universo y la nada, lo tangible y lo imaginable; ideas que permearon la filosofía cristiana muy promulgada por Europa, que entraba en conflicto con las ideas que llegaban de Oriente, con el islamismo y el ingenioso sistema indo-arábigo.
El sistema numérico de los griegos, desarrollado alrededor del siglo V a. C., no necesitaba de la presencia del cero. Además era muy complejo de usar, ya que sus símbolos no permitían realizar cálculos con ellos, de manera que las operaciones se realizaban con elementos concretos como los dedos de las manos, el ábaco o tablas de contar. La aritmética que desarrollaron estuvo a cargo, principalmente, de los mercaderes y comerciantes. Sobre los métodos que usaban los griegos para llevar las cuentas, Kaplan (2004) menciona:
Nada no era una cosa, un número, sino una condición —muchas veces transitoria— de parte de la tabla. Lo mismo ocurría con el cálculo con los dedos, […] allí, el cero se indicaba por la posición relajada o normal de los dedos: en otras palabras, no era un gesto. (p. 42)
De otro lado, el sistema numérico indo-arábigo era susceptible a los fraudes, ya que sus cifras se podían fácilmente alterar, particularmente el cero con una pequeña modificación se podía hacer pasar por un 6 o un 9, razones suficientes para que fuera prohibido su uso en Florencia en el año 1299 (Barrow, 2012; Burton, 2011).
Finalmente, los métodos poco prácticos para realizar cálculos con el ábaco, populares en la Europa medieval, perdieron poco a poco la contienda con la aritmética usada con los números indo-arábigos y la comprensión del cero como número, ideas fundamentales para el renacimiento de la matemática y la ciencia en el mundo (Ifrah, 1987; Rotman, 1993; Webb, 2015).
Para algunos, como lo expone Jaouiche (2011), el cero no fue considerado un número hasta la axiomatización de los números naturales en el siglo XIX, formulada por el matemático italiano Giuseppe Peano con el ánimo de dar una estructura rigurosa a la aritmética y, en consecuencia, a la matemática en general. Según Segre (1994), la primera versión de los axiomas fue presentada por Peano en 1889 en su libro Arithmetices principia, nova methodo exposita, que con el tiempo fueron ligeramente modificados hasta la versión final en la que se encuentra el cero, no como un objeto que se pueda definir, sino considerado formalmente como un número, aun cuando históricamente su invención sea de siglos atrás.
Consideraciones finales
Históricamente se pueden identificar varias interpretaciones del cero, que le otorgan un sentido especial sobre los demás números. Gracias a los primeros registros escritos del cero en Egipto —aún sin considerarse un número—, se evidenció que era interpretado como valor de referencia y como signo de equilibrio (Joseph, 2008; Lumpkin, 2004). En Babilonia el cero aparece como marcador posicional, debido a la necesidad que surgió en el sistema numérico de separar los símbolos y representar una posición vacía (Burton, 2011; Ifrah, 1987; Kaplan, 2004). En China lo relacionaron con la ausencia de elementos y, aunque no lograron desarrollar un símbolo para representarlo, comprendieron su uso (Ifrah, 1987; Nieder, 2016).
Además, los mayas en Mesoamérica desarrollaron un sistema numérico representado por niveles de manera vertical (Fedriani & Tenorio, 2004), lo que promovió la creación de un símbolo para expresar cuándo un nivel estaba completo y podía pasarse al siguiente (Duque, 2013; Sharer, 2003). De esta manera, lograron interpretar el cero como plenitud, estado completo o perfección, con el uso de una concha de caracol para simbolizarlo. Por otra parte, los incas no desarrollaron un lenguaje escrito para su sistema numérico. Ellos empleaban nudos en cuerdas —quipus— para llevar sus cuentas, en las que era necesario dejar un espacio vacío interpretado como la ausencia de unidades (Burton, 2011; Gutiérrez, 2009; Schmidt & Santos, 2016).
La construcción histórica y epistemológica del cero es un referente importante sobre las dificultades y problemas relacionados con su consolidación como número, ya que fue un proceso largo y complejo de más de dos milenios de historia (D’Amore & Fandiño, 2012). Su origen un poco confuso y diferente al de los demás números naturales no estaba ligado a la representación de algún objeto concreto (Stewart, 2016), por lo que fue necesario un estado superior de abstracción para que fuera aceptado como número (Berlinghoff & Gouvêa, 2010).
Estos problemas en torno al cero se pueden considerar como obstáculos epistemológicos para su aprendizaje, lo que puede influir negativamente en la percepción del estudiante frente a su conceptualización. En este sentido, el futuro docente en matemáticas debe contar con las herramientas necesarias en su formación para tomar una postura crítica frente a la enseñanza de las matemáticas, razón por la cual se considera pertinente el estudio histórico y epistemológico del cero para analizar las posibles interpretaciones que le confieren los estudiantes en formación inicial cuando proponen situaciones de enseñanza para el cero.
Referencias
Aczel, A. (2016). En busca del cero: la odisea de un matemático para revelar el origen de los números (Trad. J. Grau). Barcelona: Biblioteca Buridán.
Armengol, V. (2010). Los incas. Madrid: Tikal, Susaeta Ediciones.
Asimov, I. (2000). De los números y su historia (Trad. F. Rodríguez). Buenos Aires: El Ateneo.
Barrow, J. (2012). El libro de la nada (Trad. J. García). Barcelona: Crítica.
Bell, E. (2004). Historia de las matemáticas (Trad. R. Ortiz). México: Fondo de Cultura Económica.
Berggren, J. (1986). Episodes in the mathematics of medieval Islam. New York: Springer-Verlag. doi:10.1007/978-1-4612-4608-4
Berlinghoff, W., & Gouvêa, F. (2010). A matemática através dos tempos: um guia fácil e prático para professores e entusiastas. (Trad. E. Gomide & H. Castro,). São Paulo: Edgard Blucher.
Betti, R. (2017). Z for Zero. Lettera Matematica, 5(2), 217-220. https://doi.org/10.1007/s40329-017-0180-6
Bodleian Libraries, University of Oxford. (2017). Carbon dating finds Bakhshali manuscript contains oldest recorded origins of the symbol ‘zero’. Recuperado de https://www.bodleian.ox.ac.uk/bodley/news/2017/sep-14
Burton, D. (2011). The History of mathematics (7th ed). New York: McGraw-Hill.
Castillo, R. (2011). Aryabhata, Brahmagupta y Bhaskara. Tres matemáticos de la India. Madrid: Nivola.
Ciro, O. (2011). Historia y Epistemología del número. Bogotá: Fibonacci.
Cœdès, G. (1931). À propos de l’origine des chiffres arabes. Bulletin of the School of Oriental Studies, University of London, 6(2), 323-328. Recuperado de http://www.jstor.org/stable/607661
Colerus, E. (1943) Historia de la matemática: de Pitágoras a Hilbert (Trad. N. Caplan). Buenos Aires: Progreso y Cultura.
Collette, J. (1991). Historia de las matemáticas (Vol. I). Madrid: Siglo XXI Editores.
D’Amore, B., & Fandiño, M. (2012). El número cero: aspectos históricos, epistemológicos, filosóficos, conceptuales y didácticos del número más misterioso. Bogotá: Corporación Editorial Magisterio.
Dantzig, T. (1971). El número: Lenguaje de la ciencia (Trad. M. Balanzat). Buenos Aires: Hobbs, Sudamericana S. A.
Diller, A. (1996). New Zeros and Old Khmer. Mon-Khmer Studies Journal, 25, 125-132. Recuperado de http://sealang.net/sala/archives/pdf8/diller1996new.pdf
Divakaran, P. (2018). The Mathematics of India: Concepts, Methods, Connections. Singapore, New Dehli: Springer Hindustan Book Agency. doi:10.1007/978-981-13-1774-3
Doval, H. (2005). El nacimiento de los números y el cero. Del ábaco decimal a la computadora digital binaria. Revista argentina de cardiología, 73(4), 321-324. Recuperado de http://www.scielo.org.ar/scielo.php?script=sci_arttext&pid=S1850-37482005000400015
Duque, H. (2013). El sentido del número en la cultura maya (Tesis de maestría, Universidad Tecnológica de Pereira, Pereira, Colombia).
Fedriani, E., & Tenorio, A. (2004). Los sistemas de numeración maya, azteca e inca. Lecturas matemáticas, 25(2), 159-190.
Gómez, B. (1993). Numeración y cálculo. Madrid: Síntesis.
Gómez, C. (2009). Matemáticas en la antigua China: una isla en el mar. Sevilla: Servicio de Publicaciones Universidad de Sevilla.
González, F., Martín, M., & Silván, E. (2010). Prehistoria de la matemática y mente moderna: pensamiento matemático y recursividad en el Paleolítico franco-cantábrico. Dynamis, 30, 167-195.
Gutiérrez, T. (2009). Las matemáticas a lo largo de la historia de la prehistoria a la Antigua Grecia. Madrid: Vision Libros.
Ifrah, G. (1987). Las cifras: historia de una gran invención. Madrid: Alianza.
Jaouiche, K. (2011). India’s contribution to Arab mathematics. Indian Journal of History of Science, 46(2), 189 - 204.
Jaramago, M. (2008). El Papiro Boulaq: una síntesis actualizada. [Figura]. Recuperado de http://egiptologia.com/papiro-boulaq-sintesis-actualizada/
Joseph, G. (2008). A Brief History of Zero. Tarikh-e Elm: Iranian Journal for the History of Science, 6(1), 37-48.
Kaplan, R. (2004). Una historia natural del cero: la nada que existe. México: Océano.
Katz, V. (2009). A history of mathematics: an introduction. Boston: Addison-Wesley.
Lam, L. (1988). A Chinese genesis: Rewriting the history of our numeral system. Archive for History of Exact Sciences, 38(2), 101-108. https://doi.org/10.1007/BF00348453
Logan, R. (2017). P.S.: The importance of nothing. Zero was the gift from the East that made the scientific revolution in the West possible. Progress in Biophysics and Molecular Biology, 131, 500-503. https://doi.org/10.1016/j.pbiomolbio.2017.09.020
Lumpkin, B. (2004). The mathematical legacy of ancient Egypt: A response to Robert Palter. Recuperado de www.ethnomath.org/resources/lumpkin1997.pdf.
Mankiewicz, R. (2005). Historia de las matemáticas: Del cálculo al caos. Barcelona: Paidós Ibérica.
Nieder, A. (2016). Representing Something Out of Nothing: The Dawning of Zero. Trends in Cognitive Sciences, 20(11), 830-842. https://doi.org/10.1016/j.tics.2016.08.008
Paulos, J. (1993). Más allá de los números: meditaciones de un matemático (Trad. J. Llosa). Barcelona: Tusquets.
Pilgaonkar, S. (2014). The Khipu-Based Numeration System. Recuperado de https://arxiv.org/abs/1405.6093
Pogliani, L., Randic, M., & Trinajstić, N. (1998). Much ado about nothing—an introductive inquiry about zero. International Journal of Mathematical Education in Science and Technology, 29(5), 729-744. doi:10.1080/0020739980290509
Puttaswamy, T. (2012). Mathematical achievements of pre-modern Indian mathematicians. London Waltham: Elsevier.
Ríbnikov, K. (1987). Historia de las matemáticas (Trad. C. Valdés). Moscú: Mir.
Romig, H. (1924). Discussions: Early History of Division by Zero. The American Mathematical Monthly, 31(8), 387-389. doi:10.2307/2298825
Rotman, B. (1993). Signifying nothing: the semiotics of zero. California: Stanford University Press.
Schmidt, P., & Santos dos, J. (2016). O uso dos quipus como ferramenta de controle tributário e de accountability dos incas. Revista Brasileira de Gestão de Negócios, 19(66), 613-626. doi:10.7819/rbgn.v0i0.3099
Segre, M. (1994). Peano’s Axioms in their Historical Context. Archive for History of Exact Sciences, 48(3/4), 201-342. https://doi.org/10.1007/BF00375085
Seife, C. (2006). Cero. La biografía de una idea peligrosa (Trad. S. Zimmermann,). Madrid: Ellago.
Sen, S., & Agarwal, R. (2015). Zero: a landmark discovery, the dreadful void, and the ultimate mind. Amsterdam: Academic Press.
Sharer, R. (2003). La civilización maya (3a ed.). México: Fondo de Cultura Económica.
Sigler, L. (2012). Fibonacci’s Liber Abaci: A Translation into Modern English of Leonardo Pisano’s Book of Calculation. Nueva York: Springer. doi 1O.1007/978-1-4613-0079-3.
Stewart, I. (2012). Historia de las matemáticas: en los últimos 10.000 años. Barcelona: Crítica.
Stewart, I. (2016). Números increíbles (Trad. L. Sánchez). Barcelona: Crítica.
Vogel, K. (1966). Principios de la contabilidad hindú. Kushyar Ibn Labban, Martin Levey, Marvin Petruck. Isis, 57(1), 129-131. doi: 10.1086 / 350094
Waerden, B. (1988). Science Awakening I (Trad. A. Dresden). Dordrecht: Springer Netherlands.
Webb, J. (2015). Nada, del cero absoluto al olvido cósmico: reflexiones insólitas acerca de la nada (Trad. D. Otero-Piñero). Madrid: Alianza Editorial.

 , Lida Esperanza Riscanevo Espitia
, Lida Esperanza Riscanevo Espitia 





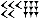


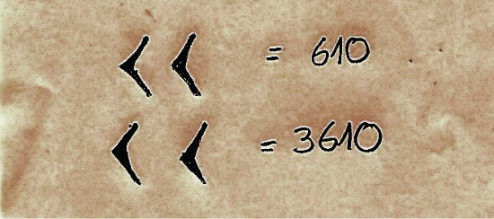
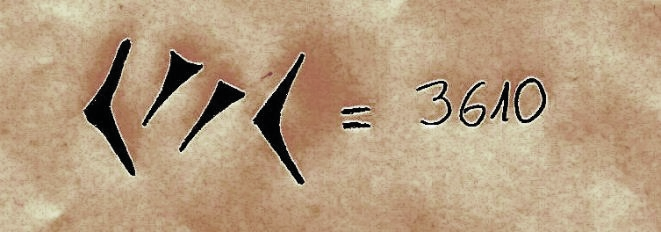

 para el cero (
para el cero (