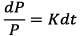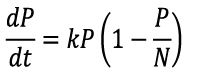Verificar la solución obtenida. Estas etapas no necesariamente deben presentarse todas siempre, o en algún orden preestablecido. Puede darse el caso en que se presenten solo algunas, en distinto orden, o de manera reiterada durante todo el proceso de resolución de algún problema en particular.
Otro aspecto que debe estar presente durante la resolución de problemas es la metacognición. Según Schoenfeld (1992), el pensamiento metacognitivo sirve para monitorear, controlar y dirigir el propio proceso cognitivo. Lo que se espera respecto a la metacognición es que el estudiante durante todo el proceso de resolución de determinado problema esté en capacidad de diseñar una estrategia de trabajo, de modo que controle sus acciones, las modifique, las refuerce o las ajuste, según sea el caso, y además se den las condiciones para replicarlas o rediseñarlas en diversos contextos.
La resolución de problemas como generadora de la actividad matemática en el aula: experimentación-conjetura-prueba-refutación-aplicación
Las matemáticas son una herramienta fundamental para descubrir el mundo o adaptarlo. Esto es posible mediante la solución de problemas, que se han presentado desde que el ser humano tuvo conciencia de sí mismo. Polya (1981) afirma que tener un problema es buscar de forma consciente una acción apropiada para lograr un objetivo claramente concebido pero no alcanzable de forma inmediata. Posamentier (1998) establece que un problema es una situación que confronta una persona, que requiere una respuesta y para el cual los caminos de salida no son conocidos inmediatamente.
En efecto, las ecuaciones diferenciales ofrecen diferentes retos, desde la concepción de una hipótesis para plantear un modelo, pasando por las estrategias de resolución del sistema o la ecuación diferencial que derive del modelo en el mismo análisis cualitativo, hasta la recopilación de todos los resultados obtenidos del proceso. En este punto, se hace necesario tener una estrategia a partir de la comprensión de una determinada situación, valerse de las heurísticas para proponer o refinar un modelo, validarlo y confrontar las posibles soluciones con datos reales con el fin de probar la eficiencia del método empleado en la resolución del problema (Iglesias, 2017). Como se puede apreciar, para resolver un problema se requiere proponer una o varias conjeturas, las cuales deben ponerse a prueba mediante algunos ejemplos y contraejemplos con el ánimo de verificarlas, refutarlas o reformularlas, según sea el caso (Lakatos, 1978). En este proceso se presentan las heurísticas, así como las fases planteadas por Polya (1981), de manera indistinta.
De otra parte, en los últimos años, los avances tecnológicos —especialmente en las computadoras— han ocasionado que la enseñanza de la matemática en cursos de ecuaciones diferenciales pueda contar con una metodología propia de las ciencias experimentales, en el sentido de poder experimentar y comprobar (Hernández et al., 2016).
Cuando se observan las dificultades existentes en cursos de ecuaciones diferenciales porque no cumplen con las expectativas, ni se adaptan a las necesidades concretas de los estudiantes, se apela a la incorporación de la tecnología para promover la conexión entre las distintas partes de la matemática, resolver problemas con aplicaciones al mundo real, dominar métodos numéricos e interpretar líneas de fase y campos de pendientes (Bejarano, 2019).
Los estudiantes normalmente no se han habituado a la elaboración e interpretación de las gráficas, por lo que se espera que mediante la inclusión de recursos tecnológicos en los cursos de ecuaciones diferenciales puedan establecer conjeturas a partir de la visualización de los campos de pendientes y las líneas de fase para interpretar alguna solución y su comportamiento (León, 2017). Una herramienta empleada en el enfoque cualitativo para el tratamiento de las ecuaciones diferenciales tiene que ver con los métodos numéricos (Abell & Braselton, 2014).
Otro elemento importante de los temas de la matemática aplicada, como lo son las ecuaciones diferenciales, tiene que ver con la experimentación, ya que esta permite de algún modo hacer concretas para los estudiantes ciertas situaciones problematizadoras, que de otra manera dificultarían la comprensión y tratamiento por parte de ellos y, a su vez, la exposición de los temas para el profesor (Lesh, Galbraith, Haines & Hurford, 2013).
Ciertos problemas típicos de las ecuaciones diferenciales, como el vaciado de un tanque, la caída de los cuerpos y el crecimiento de ciertas poblaciones, pueden fácilmente ser representadas en aula con recursos económicos, de fácil acceso e incluso con niños pequeños (Parra, 2016).
Metodología
Este trabajo se hizo con un enfoque cualitativo. Se diseñó y se validó un modelo didáctico para el proceso de enseñanza-aprendizaje de las ecuaciones diferenciales. La información se analizó utilizando Atlas ti.
Población.
Los estudiantes de las carreras de ingeniería generalmente toman el curso de ecuaciones diferenciales durante el cuarto semestre. Participaron en esta investigación cinco estudiantes de una universidad privada en Colombia, quienes se identifican para esta investigación como Yésica, David, Fabio, Juan y Paola. Las edades estaban entre los 20 y 22 años. En los anteriores semestres, estos estudiantes ya habían asistido a cursos de cálculo diferencial e integral, cada uno de los cuales consta de 96 horas, y al curso de álgebra lineal, con una duración de 64 horas. Estas asignaturas son prerrequisito para tomar ecuaciones diferenciales. Este curso habitualmente se lleva a cabo durante un semestre académico que consta de 16 semanas, con una intensidad horaria de 4 horas semanales, para un total de 64 horas presenciales. Esta implementación se llevó a cabo durante todo un semestre académico.
Modelo didáctico.
Un modelo didáctico es una representación del proceso de enseñanza-aprendizaje en un contexto científico y sociocultural determinado basado en opciones epistemológicas y éticas específicas (Mayorga & Madrid, 2010). El modelo propuesto se enfoca en el aprendizaje más que en la enseñanza, y se desarrolla a partir de lo mostrado en la figura 2.
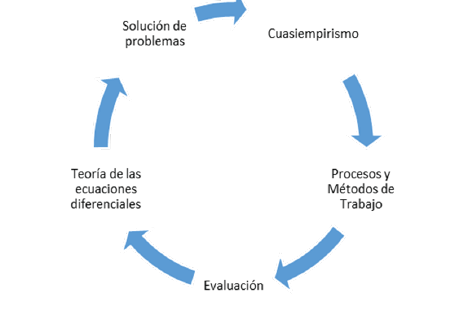
Figura 2. Proceso de aprendizaje. Fuente: elaboración propia.
Este proceso no es lineal, por consiguiente se pueden hacer saltos hacia adelante o hacia atrás (Mayorga & Madrid, 2010). Con base en los elementos mencionados se estableció un modelo didáctico inicial que se puso a prueba durante el curso de ecuaciones diferenciales.
Esta investigación se enfoca en el aprendizaje más que en la enseñanza y se desarrolla a partir de los siguientes elementos (figura 3).
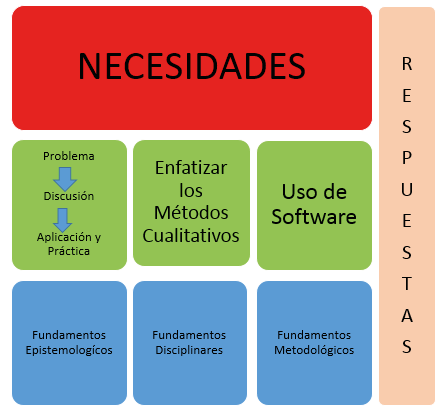
Figura 3: Modelo didáctico preliminar. Fuente: elaboración propia.
Los métodos empleados en el curso de ecuaciones diferenciales desde un enfoque cualitativo se orientan intencionalmente a que los alumnos lleven a cabo actividad matemática, y a que de esta manera comprendan el comportamiento de las soluciones de ciertas ecuaciones diferenciales y algunos sistemas (Blanchard, Devaney & Hall, 1999; Hirsch, 2004). Dado que se estudian las ecuaciones diferenciales desde la concepción cuasiempírica de las matemáticas, el alumno continuamente tiene que experimentar, conjeturar, diseñar y contrastar modelos y formular y comprobar generalizaciones (Lakatos, 1978), lo que enfatiza el papel protagónico del estudiante en la construcción de conocimiento y del docente como mediador (Moreno & Azcárate, 2003).
Inicialmente, se realizó una evaluación diagnóstica de lo que el alumno ya puede hacer o sabe sobre ecuaciones diferenciales, desde un enfoque cualitativo y con el enfoque cuasiempírico de las matemáticas.
La evaluación de los procedimientos se llevó a cabo en tres diferentes aspectos:
- Comportamiento cualitativo de las ecuaciones diferenciales de primer orden.
- Comportamiento cualitativo de los sistemas de ecuaciones diferenciales lineales de primer orden.
- Comportamiento cualitativo de los sistemas de ecuaciones diferenciales no lineales de primer orden.
Los instrumentos empleados para evaluar los aprendizajes de los temas anteriores son los planes de clase o actividades de trabajo, de manera individual y grupal.
Inicialmente se elaboró el esquema mostrado en la figura 3, que recoge los elementos de un modelo didáctico (Mayorga & Madrid, 2010), sirve como guía inicial para el diseño del curso de ecuaciones diferenciales desde un enfoque cualitativo y es confrontado posteriormente mediante su implementación en un curso de ecuaciones diferenciales.
El modelo didáctico parte de una situación inicial del estudiante. Dicha situación se traduce en la necesidad de tomar el curso de ecuaciones diferenciales. Además, es ideal que los estudiantes realmente se apropien de los contenidos del curso con una alta motivación y en el contexto de la resolución de problemas. Otros aspectos implícitos en las necesidades —de acuerdo con la experiencia del autor— van más allá del estudiante y tienen que ver con unos planes de estudio y prácticas docentes muchas veces desactualizados. Así mismo, el trabajo en aula continúa evidenciando un rol protagónico por parte del docente y en muchos casos se desconoce el potencial de los estudiantes (Bravo, 2005; Moreno & Azcárate, 2003). Es común que los estudiantes se abstraigan de su proceso de aprendizaje y estén desmotivados, y que como sujetos pasivos pongan en manos de la suerte y del docente los resultados del curso de ecuaciones diferenciales.
Una vez enunciados aquellos aspectos considerados como deficiencias del proceso enseñanza-aprendizaje de las ecuaciones diferenciales, se establecieron los fundamentos para nuestro modelo didáctico. La propuesta cuenta con tres elementos articuladores: solución de problemas (Polya, 1981), enfoque cuasiempírico de las matemáticas (Lakatos, 1978) y la teoría cualitativa de las ecuaciones diferenciales (Delshams, 2004), que se implementa apoyada en el uso del software.
Por ser las ecuaciones diferenciales una herramienta versátil y funcional en la modelación de diversas situaciones problema propias de las ciencias en general (Bejarano, 2019), brindan un ambiente ideal para su aprendizaje desde el enfoque cuasiempírico de las matemáticas, el cual inicia con la formulación del modelo y llega hasta la exploración de las posibles soluciones de un problema, que no surgen automáticamente; más bien son producto de arduas discusiones e interpretaciones, como lo señala este enfoque (Lakatos, 1978).
Desde luego, la teoría cualitativa de las ecuaciones diferenciales se nutre del cuasiempirismo, debido a que durante el proceso necesario para encontrar las posibles soluciones de un problema se parte de una conjetura (Lakatos, 1978), sin tener total certeza acerca de su validez, sino que dicha conjetura debe ser evaluada y validada, o en otros casos reformulada o refutada.
La implementación del modelo se realizó mediante el diseño de seis planes de clase, es decir, guías para los estudiantes.
Recolección y análisis de los datos.
Una vez establecido el modelo didáctico empleado para esta investigación, se puso en práctica en el aula de clase con el fin de verificar su validez. Se recolectaron los datos mediante observación directa, entrevistas y análisis de registros y planes de clase. El análisis se hizo con uso de Atlas ti. Se establecieron códigos que permitieron generar una teoría o modelo didáctico —en este caso particular— (Sampieri, Fernández & Baptista, 2014).
Resultados
Se describe inicialmente el trabajo de los estudiantes en uno de los planes de clase y luego el funcionamiento del modelo a través de la codificación realizada en Atlas ti.
Trabajo de los estudiantes.
Para el curso completo se diseñaron seis planes de clase. A continuación se describe el trabajo de los estudiantes en uno de ellos y se muestra cómo los estudiantes emplearon los cuatro pasos de Polya (1981) en la solución de problemas. Se ejemplifica con un problema sobre crecimiento de la población de Estados Unidos tomado de Blanchard, Devaney y Hall (1999).
- Comprender el problema, como se evidencia en el plan de clase Crecimiento de una población: luego de alguna discusión, los estudiantes, orientados por el profesor, concluyeron que era posible modelar el crecimiento de la población de los Estados Unidos mediante la ecuación diferencial
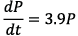 .
. - Concebir un plan: en este momento surgieron varias posibilidades, por ejemplo, Yésika creía que el término se podía pasar a multiplicar a la derecha y la debía pasar a dividir a la izquierda así:
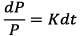 .
. - Ejecutar el plan: luego de algunos minutos, los estudiantes lograron resolver la ecuación diferencial, de donde resultó: P(t)=cekt. Los estudiantes quedaron preocupados debido a que tenían muchos términos desconocidos en el modelo, de donde surgió el interrogante: ¿cómo encontrar los valores de los parámetros c y k? Fabio recordó que en la prueba de entrada, cuando se había estudiado el movimiento de una pelota lanzada hacia arriba, resultó una constante de integración cuyo valor se encontró al reemplazar la velocidad inicial. Entonces él concluyó que se podía emplear la población inicial y así obtuvieron: P(t)=3,9 ekt
Luego, David creyó que para hallar el valor de k se podía emplear otra condición de las que se encontraban en la tabla. Se sabía que 10 años después, es decir en 1800, la población era de 5.3 millones de personas. De esta manera la función P(t) sería: P(t)=3,9 e0,3067t
- Verificar la solución: los cinco estudiantes realizaron los cálculos, pero observaron que desde la década de 1870 en adelante la diferencia entre la población real y la calculada según el modelo se hacía cada vez mayor. Entonces surgió la pregunta: ¿por qué falló nuestro modelo? Juan afirmó que efectivamente el modelo era de crecimiento exponencial y en poco tiempo la población crecía muy rápidamente. Yésika resaltó que el modelo era muy sencillo y no tenía en cuenta la mortalidad y los recursos. David creyó que este modelo funcionaba para poblaciones pequeñas y tiempos cortos.
Como se puede apreciar, no solamente se evidenciaron los cuatro pasos del método de Polya (1981), sino, además, desde el planteamiento mismo del modelo se partió de conjeturas que debían ser validadas en la medida en que se resolvía el problema (Lakatos, 1978). Por otro lado, más allá de encontrar una solución analítica, lo que se privilegia es observar el comportamiento de las soluciones conforme el tiempo pasa, es decir, el análisis cualitativo (Abell & Braselton, 2014).
Una vez que los estudiantes observaron que el modelo exponencial no era funcional para resolver el problema, debido a que la población crecía sin límite, y por tanto no correspondía con los valores reales de la población de Estados Unidos, para salir del atasco y en aras de resolver el problema en cuestión, el profesor propuso la ecuación de Verhulst o logística, con k la constante de crecimiento y N son los recursos.
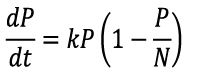
Lo que se destaca de ella es que, aun siendo algo simple, responde a la solución del problema, lo que pudieron constatar los estudiantes, quizás por considerar los recursos disponibles para la población. Además, ha funcionado satisfactoriamente para la proyección de ciertas poblaciones.
Cuando el modelo se hubo refinado, los estudiantes encontraron cierta dificultad para resolver de manera analítica dicha ecuación diferencial. Entonces, el profesor cuestionó a los estudiantes acerca de otra manera de estudiar el modelo sin necesidad de resolver la ecuación diferencial. Ahí cobró sentido el análisis cualitativo de la ecuación diferencial, es decir, se debían encontrar los puntos o soluciones de equilibrio: Juan rápidamente dijo que si P=0, se tenía una solución de equilibrio. La pregunta siguiente fue si había más soluciones de equilibrio. La respuesta a esta pregunta no surgió tan rápidamente como la anterior.
Después de pensarlo algún tiempo, Fabio creyó que P=N era otra solución de equilibrio, lo cual efectivamente era cierto. Luego cada estudiante debía bosquejar las soluciones junto con las soluciones de equilibrio en el plano P-t . A los cinco estudiantes les resultó relativamente fácil bosquejar las soluciones de equilibrio, pero se preguntaron cómo bosquejar otras soluciones.
Juan afirmó que si la población aumentaba haciéndose mayor que N, lo que estaba en el paréntesis tenía signo negativo, y como P y k eran positivos, se concluyó que la población decrecía. Por otro lado si N>P, lo que estaba en paréntesis tendía a 1 y P se acercaba a 0, lo cual significó que se obtendría nuevamente la ecuación de crecimiento exponencial, que, como se vio, solo funcionaba para poblaciones muy pequeñas. David dijo que si 0<P<N, la población iba creciendo hasta acercarse a N.
Una vez agotada la discusión, los estudiantes tenían la oportunidad de contrastar sus conjeturas con los campos de pendientes elaborados en Maple ® (figura 4).
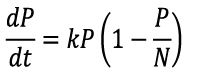
Figura 4. Campo de pendientes de la ecuación de Verhulst elaborado por estudiantes. Fuente: elaboración propia.
En este punto, cabe resaltar que se han evidenciado los principales elementos que hacen parte del modelo para el aprendizaje de las ecuaciones diferenciales: la resolución de problemas, el cuasiempirismo y el análisis cualitativo por medio de la tecnología (Abell & Braselton, 2014; Lakatos, 1978).
En la tabla 1 se resumen los logros más relevantes de la elaboración y valoración del modelo didáctico propuesto.
Tabla 1
Logros relevantes de los estudiantes
Elementos del modelo didáctico | Características de los procesos de aprendizaje | Aportes del modelo didáctico |
1. La resolución de problemas 2. El cuasiempirismo 3. El análisis cualitativo empleando la tecnología | 1. La intuición como ruta al descubrimiento 2. El pensamiento geométrico como elemento sintetizador 3. La conjetura como elemento generador 4. Consolidación del aprendizaje mediante la práctica | 1. Empoderamiento de los estudiantes 2. Métodos cualitativos a través de la tecnología 3. Uso de conjeturas 4. Solución de problemas |
Fuente: elaboración propia.
Validación del modelo
A través de Atlas ti, surgió el siguiente mapa (figura 5) a partir de los códigos establecidos, que muestra las relaciones entre los elementos del modelo propuesto. 
Figura 5. Mapa de códigos (categorías). Fuente: elaboración propia.
A continuación, se explican brevemente las categorías que surgieron como resultado del análisis de los datos.
Solución de problemas.
Este código aparece en el primer nivel por dos razones: una primera tiene que ver con el hecho de que se estableció como elemento transversal para todo el curso por su pertinencia; de otro lado, se interrelaciona permanentemente con la postura teórica del cuasiempirismo (Ernest, 2004).
Cada plan de clases inicia con una situación problema, la cual obliga a que los estudiantes propongan conjeturas y las discutan con sus compañeros y el docente, a fin de establecer el modelo que mejor responda al problema. El paso a seguir consiste en resolver la ecuación o sistema de ecuaciones diferenciales, lo cual se hizo desde el enfoque cualitativo. En algunos casos se emplearon los métodos numéricos e incluso los analíticos si era posible, con el fin de obtener un completo panorama del problema en cuestión, como lo sugieren Abell y Braselton (2014).
Cabe resaltar que, una vez propuesto el problema de cada plan de clase, los estudiantes de manera natural se situaron en las cuatro fases propuestas por Polya (1981). Por ejemplo, para estudiar el crecimiento de una población es necesario comprender plenamente la situación, es decir, clase de población, datos estadísticos o valores iniciales con que se cuentan, qué factores inciden en el crecimiento de una población, para luego establecer un plan, o sea, encontrar la ecuación diferencial que modela el problema (Braun, 1983). Después se debe resolver la ecuación diferencial, lo cual se hace de manera cualitativa con ayuda de la tecnología —Maple 18®— y se debe contrastar la solución con los datos reales con el fin de verificar la validez del proceso (Hernández, et al., 2016).
Concepción cuasiempírica de las matemáticas.
Una vez propuesto el problema inicial de cada plan de clases a partir de preguntas generadoras, los estudiantes enunciaron valiosas conjeturas que discutieron entre ellos mismos y con el docente, de modo que se pudiera establecer un modelo inicial. Después de plantear la o las ecuaciones diferenciales que modelan el problema, se debe proceder a resolver, privilegiando los métodos cualitativos, lo cual también da lugar a conjeturas o experimentación. Los estudiantes conjeturan acerca de las soluciones, sus características y comportamiento en el tiempo (Abell & Braselton, 2014; Trigueros, 2009). Esto se enmarca en una postura falibilista de las matemáticas (Hersh, 1999).
Métodos cualitativos.
El curso de ecuaciones diferenciales estuvo orientado con el enfoque cualitativo, lo cual resultó motivante e interesante para los participantes, por dos razones. Primero, no es necesario que memoricen las estructuras de las ecuaciones diferenciales que se pueden resolver analíticamente ni tampoco los algoritmos de resolución empleados. En segundo lugar, debido a que los métodos cualitativos se basan en el pensamiento geométrico, resulta mucho más sencillo para ellos diagramar en un computador un campo vectorial, una línea de fase o graficar una solución numérica, lo cual, además, en ciertos casos es más evidente y enriquecedor que una función que represente la solución de una ecuación diferencial —claro, siempre que esta se pueda encontrar—.
Uso de tecnología.
Para esta investigación es indispensable el uso de un software. En este caso, para el curso de ecuaciones diferenciales, se empleó Maple 18®, debido al potencial que posee para el estudio de las ecuaciones diferenciales y su fácil manejo (Hernández, et al., 2016).
El uso de Maple 18® produjo grandes beneficios, no solamente por lo motivados que se perciben los estudiantes, sino que además les permite caracterizar el comportamiento de la solución de un sistema dinámico de forma muy ilustrativa, comprensible y rápida, aun cuando no se encuentre la solución exacta de manera analítica.
Lo que se observó como debilidad en la prueba de entrada realizada por los estudiantes, en relación con la escasa comprensión del concepto de derivada, se resolvió a lo largo del curso gracias a que el análisis cualitativo apoyado en el software resultó un ejercicio rutinario y muy enriquecedor para ellos, ya que de allí se desprendía todo el análisis posterior de las soluciones del problema y sus posibles variaciones, como lo muestran Abell y Braselton (2014).
Finalmente se concluye que esta investigación culminó con los siguientes logros:
- La elaboración de un modelo didáctico para el aprendizaje de las ecuaciones diferenciales desde un enfoque cualitativo basado en el cuasiempirismo.
- Se logró evidenciar de primera mano el proceso de aprendizaje del grupo de cinco estudiantes que participaron del curso, lo cual resulta novedoso, debido a que, si bien en otras latitudes existe alguna referencia acerca de algún curso de ecuaciones diferenciales con enfoque cualitativo, no se tienen registros acerca de su implementación completa desde el cuasiempirismo como teoría de la educación matemática.
- El enfoque de solución de problemas es ideal para el curso de ecuaciones diferenciales basado en el cuasiempirismo, como lo señalan Abell y Braselton (2014), ya que entre ellos se genera una dialéctica, es decir, ante una situación problema se parte de una conjetura para proponer una vía de solución al problema. Dicha conjetura se pone a prueba o se socializa. Si no soporta la prueba, debe ser revisada con el fin de mejorarla o refutarla (Lakatos, 1978). Al proponer una solución al problema también se conjetura, si la solución resulta. De la misma manera, se debe conjeturar qué ocurre con las soluciones con el paso del tiempo, o si se cambian las condiciones o los parámetros (Hirsch, Smale & Devaney 2004).
- La potencia del concepto de la derivada como la pendiente de la recta tangente se hace latente en el análisis cualitativo. Cuando los estudiantes elaboran el campo vectorial, se aprecia en toda su magnitud el comportamiento de las soluciones y con algo de álgebra se puede tener un panorama completo acerca de todas las soluciones de una ecuación diferencial o de un sistema de ecuaciones diferenciales. Esto también permitió ver la importancia de usar software para realizar este tipo de análisis, como lo señalan Hernández, et al. (2016).
- El trabajo exhaustivo y sistemático del método cualitativo, complementado con los métodos numéricos y analíticos, favorece la comprensión de los estudiantes acerca de cada situación problema y sus soluciones (Abell & Braselton, 2014). Además, brinda alternativas frente a un atascamiento, es decir, que cuando ellos se encuentran con una ecuación diferencial o un sistema de ecuaciones diferenciales que surge como modelo para cierto problema y no es posible encontrar una solución analítica, lo cual es frecuente, pueden apelar a los métodos cualitativos y/o numéricos para encontrar una vía de resolución de dicho problema.
- Por otro lado, los estudiantes se hacen conscientes de que los métodos de solución de un problema no son infalibles ni absolutos.
- Un aspecto determinante, que además se considera un importante logro del curso de ecuaciones diferenciales desde un enfoque cualitativo y basado en el cuasiempirismo, consiste en que los cinco estudiantes que terminaron el curso y tenían un promedio en sus cursos previos de matemáticas rondando el tres —la nota mínima para aprobar—, en el curso de ecuaciones diferenciales obtuvieron un promedio de 3.9.
- Si bien es cierto que los logros alcanzados luego de la aplicación y valoración de la propuesta son muy positivos, cabe aclarar que en muchos casos los estudiantes se muestran muy inseguros y les cuesta participar durante la clase.
Finalmente, a partir del modelo didáctico preliminar, toda la información recolectada en los planes de clase y su respectivo análisis se concluye al presentar de modo esquemático el modelo didáctico obtenido según lo establecido por Mayorga y Madrid (2010) (figura 6).
Necesidades | Respuestas |
Desactualización | Descontextualización | Desmotivación |
Problema discusión aplicación y práctica | Métodos cualitativos | Uso de software Maple 18 |
Líneas de fase y campos de pendientes | Sistemas lineales | Sistemas no lineales y caos |
Fundamentos epistemológicos cuasiempirismo | Fundamentos disciplinares métodos cualitativos | Fundamentos metodológicos resolución de problemas |
Figura 6. Modelo didáctico consolidado. Fuente: elaboración propia.
Referencias
Abell, M., & Braselton, J. (2014). Introductory Differential Equations. Londres, Inglaterra: Academic Press.
Bejarano, A. (2019). Estrategia de reflexión para enseñanza de proyectos de construcción en Ingeniería Civil. Alteridad. Revista de Educación, 14(1), 122-137. https://dx.doi.org/10.17163/alt.v14n1.2019.10
Bender, E. (1978). An Introduction To Mathematical Modeling. San Diego, Estados Unidos: A Wiiey-Interscience Publication, John Wiley and Sons.
Blanchard, P., Devaney, R., & Hall, G. (1999). Ecuaciones diferenciales. Boston, Estados Unidos: Springer.
Braun, M. (1983). Ecuaciones diferenciales y sus aplicaciones. Nueva York, Estados Unidos: Springer.
Bravo, J. (2005). Avatares y estereotipos sobre la enseñanza de los algoritmos en matemáticas. Revista Iberoamericana de Educación Matemática, (4), 31-46.
Delshams, A. (2004). Poincaré, creador de los métodos todavía modernos en las ecuaciones diferenciales y en la mecánica celeste. Arbor, 178(704), 669-689. http://dx.doi.org/10.3989/arbor.2004.i704.555
Ernest, P. (2004). The Philosophy Of Mathematics Education. London, England: Taylor and Francis Group.
Hernández, C, Jaimes, L., & Chaves, R. (2016). Modelos de aplicación de ecuaciones diferenciales de primer orden con GeoGebra: actividades para resolver problemas de mezclas. Mundo FESC, 6(11), 7-15. Recuperado de http://www.fesc.edu.co/Revistas/OJS/index.php/mundofesc/article/view/77
Hersh, R. (1999). What is Mathematics Really?. Oxford, England: Oxford University Press.
Hirsch, M., Smale, S., & Devaney, R. (2004). Differential Equations, Dynamical System And Introduction To Chaos. San Diego, United States: Elsevier Academic Press.
Iglesias, N. (2017). Estudio exploratorio sobre la importancia de la matemática para la carrera de ingeniería civil en la Universidad de Oriente. Revista electrónica formación y calidad educativa, 5, 45-62. Recuperado de http://www.refcale.uleam.edu.ec/index.php/refcale/article/view/1325/883
Lakatos, I. (1978). Pruebas y refutaciones. Madrid, España: Alianza.
León, C. (2017). El pensamiento covariacional y GeoGebra: herramientas para la explicación científica de algunas realidades. Tecné, Episteme y Didaxis: TED, (42), 159-171. Recuperado de http://www.scielo.org.co/scielo.php?script=sci_arttext&pid=S0121-38142017000200159&lng=en&tlng=es
Lesh, R., Galbraith, P., Haines, C., & Hurford, A. (2013). Modeling Students’ Mathematical Modeling Competencies. Dordrecht, Países Bajos: Springer.
Mayorga, M., & Madrid, D. (2010). Modelos didácticos y estrategias de enseñanza en el Espacio Europeo de Educación Superior. Tendencias PedagóGicas, 15, 91-111. Recuperado de https://revistas.uam.es/tendenciaspedagogicas/article/view/1934
Moreno, M., & Azcárate, G. (2003). Concepciones y creencias de los profesores universitarios de matemáticas acerca de la enseñanza de las ecuaciones diferenciales. Enseñanza de las ciencias, 21(2), 265-280. Recuperado de https://www.raco.cat/index.php/Ensenanza/article/view/21935
Nápoles, J. (2004). Un siglo de teoría cualitativa de ecuaciones diferenciales. Lecturas Matemáticas, 25(1), 59-111.
Parra, M. (2016). Interacciones y contribuciones. Forma de participación de estudiantes de quinto grado en ambientes de modelación matemática. Actualidades Investigativas en Educación, 16(3), 283-310. https://dx.doi.org/10.15517/aie.v16i3.26084
Polya, G. (1981). Mathematical Discovery: On understanding, learning and teaching problem solving. New York, United States: Jhon Wiley and Sons.
Posamentier, A. (1998). Problem Solving Estrategies For Efficient and Elegant Solutions. Thousand Oaks, United States: Corwin Press.
Sampieri, R., Fernández, C., & Baptista, M. (2014). Metodología de la investigación (6ª ed.). México, Ciudad de México: McGraw Hill.
Schoenfeld, A. (1992). Learning to think mathematically. New York, United States: MacMillan.
Toro, H. (2018). Modelo para la transmisión del VIH en una población con diferenciación de sexos y usos de medidas preventivas. Revista de Matemática Teoría y Aplicaciones, 25(2), 293-318. https://dx.doi.org/10.15517/rmta.v25i2.33700
Trigueros, M. (2009). El uso de la modelación en la enseñanza de las matemáticas. Innovación Educativa, 9(46), 75-87.

 , Gerardo Antonio Chacón Guerrero
, Gerardo Antonio Chacón Guerrero 
 , se dice que el equilibrio es asintóticamente estable. Los equilibrios que no son estables se llaman equilibrios inestables.
, se dice que el equilibrio es asintóticamente estable. Los equilibrios que no son estables se llaman equilibrios inestables.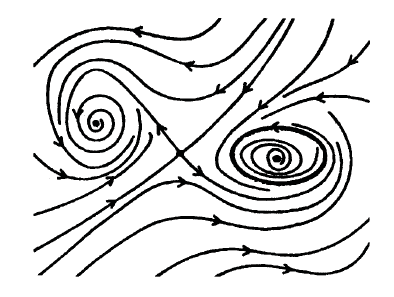


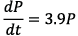 .
.