Learning by discovery in systems of special points and lines in a triangle

Abstract

The article presents the results of a research about learning the special elements in a triangle in Euclidean geometry, carried out with tenth grade students of a school in Tunja, aged between 14 and 17. The conjecturing and the characterization of these elements were analyzed based on the exploration of dynamic geometry environments designed in GeoGebra. The methodology was qualitative with descriptive-interpretative characteristics. The proposal is based on Bruner’s learning by discovery approach. The students progressed in their intuitive thinking by implementing activities focused on visualization, mediated by dynamic drawings. The results show that students learned about special lines and points in a triangle: they identified these in the graphic representation, prioritized the use of natural language, conjectured about their properties and discovered relations and properties in triangles; which caused significant learning. Thus, they advanced in the development of spatial thinking. An important element was the development of the students’ digital competence with the use of GeoGebra.

Keywords: geometric objects, conjecture, formalization, dynamic geometry

Aprendizagem por descobrimento em sistemas de pontos e retas notáveis do triangulo

Resumo

O artigo apresenta os resultados de uma pesquisa sobre a aprendizagem dos elementos notáveis do triângulo na geometria euclidiana, realizada com estudantes do décimo ano do ensino médio numa escola de Tunja, com idades entre 14 e 17 anos. Analisou-se a conjectura e a caracterização de ditos elementos, a partir da exploração de ambientes de geometria dinâmica projetada no GeoGebra. A metodologia foi qualitativa, descritiva e interpretativa. A proposta está baseada na aprendizagem por descobrimento de Bruner. Houve um progresso no pensamento intuitivo dos estudantes ao implementar as atividades focadas na visualização, mediadas com desenhos dinâmicos. Os resultados mostram que os estudantes aprenderam sobre retas e pontos notáveis do triângulo: eles os identificaram na representação gráfica, priorizaram o uso da linguagem natural, conjeturaram sobre suas propriedades e descobriram relações e propriedades dos triângulos; o que gerou uma aprendizagem significativa. Assim, os estudantes avançaram no desenvolvimento do pensamento espacial. Um item importante foi o desenvolvimento da competência digital dos estudantes com o uso do GeoGebra.

Palavras-chave: objetos geométricos, conjecturas, formalização, geometria dinâmica

Introducción

Enseñar la geometría es una tarea de gran importancia e interés, pero a la vez de bastante complejidad, debido a la diversidad de objetos y metodologías que involucra. Esto implica una gran responsabilidad de los docentes, quienes diseñan estrategias y metodologías para que los estudiantes logren un mejor aprendizaje. Particularmente, en la educación básica y media, se evidencian grandes dificultades en el aprendizaje de los objetos geométricos y en el reconocimiento de propiedades y relaciones entre estos. Al respecto Gutiérrez (2011), afirma:

Enseñar geometría en los grados de las educaciones primaria y secundaria es una tarea compleja debido a las múltiples variables que influyen. Actualmente, existe un acuerdo generalizado entre didactas de las matemáticas y profesores de matemáticas en que la enseñanza de la geometría debe basarse en metodologías que faciliten la actividad de exploración y descubrimiento de parte de los estudiantes. (p. 3)

Es importante buscar posibilidades que ayuden al aprendizaje de los estudiantes, para que pueda darse de la mejor manera, según el contexto. En este sentido, la geometría es una disciplina inmersa en otras ciencias. Por lo tanto, es posible encontrar diferentes situaciones que permitan su estudio, sin dejar de lado su formalidad y rigor. Es una rama multifacética de las matemáticas, pues guarda relación con otros dominios matemáticos, con las ciencias naturales y las ciencias sociales (Camargo & Acosta, 2012).

De otro lado, las realidades educativas actuales exigen nuevas metodologías que encaminen a un mejor aprendizaje. Por ende, es importante tener en cuenta la implementación de diferentes estrategias para una mejor comprensión de los objetos matemáticos por parte de los estudiantes. Lo anterior implica un cambio en la forma como el docente desarrolla el trabajo en el aula. De acuerdo con esto, Boude y Cárdenas (2016) afirman: “los docentes constituyen uno de los factores más importantes del proceso de formación de los estudiantes, pues son ellos quienes están día a día con los estudiantes y proponen los procesos que estos deben desarrollar para alcanzar sus competencias” (p. 29).

La investigación surge a partir de la dificultad de los estudiantes al formalizar conceptos y conjeturar sobre las propiedades de diferentes objetos geométricos. El objetivo es analizar de qué manera los estudiantes formalizan y conjeturan conceptos y propiedades relativas a rectas y puntos notables del triángulo en geometría euclidiana plana, a partir del aprendizaje por descubrimiento (Bruner, 1966) en ambientes de geometría dinámica.

La investigación está enmarcada en la línea de geometría y virtualidad del grupo de investigación Pirámide de la Universidad Pedagógica y Tecnológica de Colombia. Se destaca la importancia de esta asignatura en el currículo escolar y en el aprendizaje de la matemática por parte de los estudiantes, así como su aplicabilidad en su entorno. Por esta razón, es importante que los docentes de esta disciplina usen el pensamiento visual, el diseño de tareas y el análisis didáctico, para indagar sobre el aprendizaje de la geometría. Al respecto, Gamboa y Ballesteros (2009) comentan:

Para todo profesor de matemáticas conocer y ser consciente de la utilidad de la geometría, su desarrollo histórico y posible aplicación al mundo real, pueden convertirse en elementos pilares que guíen su práctica docente hacia la creación de situaciones problema para los estudiantes, con el fin de que la geometría adquiera un sentido tangible, que contribuya con la estimulación y desarrollo de sus capacidades de percepción espacial y visual, y que minimice las dificultades que implica su estudio. (p. 117)

En el aprendizaje de la geometría euclidiana plana, es de gran ayuda usar mediaciones que faciliten dicha labor a los estudiantes. Cada sujeto aprende de manera diferente a los demás, lo cual implica que se deban tener en cuenta varias formas y recursos para la enseñanza, como el uso de materiales reales, de dibujo y ambientes de geometría dinámica, de tal manera que se pueda lograr una mayor coherencia en los procesos educativos. En este sentido, es importante que los elementos tecnológicos propicien mejores aprendizajes. Tal es el caso de los ambientes virtuales, que son llamativos para los estudiantes y que les permiten interactuar con el docente y con las temáticas que desean aprender. En este caso, se trabajará la geometría dinámica mediante el software GeoGebra, por medio del cual es posible analizar con mayor claridad diferentes objetos geométricos relacionados con las rectas y puntos notables del triángulo. “La geometría dinámica ofrece la oportunidad de trabajar con construcciones geométricas en un entorno que tiene correspondencia directa con el contexto de la geometría euclidiana” (Samper & Toro, 2017, p. 373).

Los ambientes de geometría dinámica proporcionan un material que explota el pensamiento visual para explorar los sistemas semióticos gráficos como base para expresar propiedades en lenguaje natural, con miras a formalizar los conceptos geométricos. Para esta investigación se parte del supuesto sobre la bondad didáctica de las herramientas tecnológicas y virtuales para mejorar el proceso de aprendizaje de los estudiantes, ya que podría permitirles una mejor comprensión de los objetos geométricos estudiados a través de la experiencia de aula, puesto que “la introducción de las TIC en el contexto educativo ha dado un nuevo impulso a la pedagogía, estimulando al sistema escolar en la búsqueda de nuevos caminos para aprender” (Correa & Pablos, 2009, p. 134).

La incorporación de las TIC en el aula, como mediadoras en el proceso de aprendizaje de los estudiantes, permite al docente valorar y reflexionar sobre su eficacia en la enseñanza. De esta manera, la didáctica se ha constituido como el ámbito de organización de diversas reglas que permiten una enseñanza más eficaz (Fandos, Jiménez & González, 2002). Esto ha llevado a que en los últimos años el uso de software de geometría dinámica haya sido acogido en el aprendizaje de la geometría. “Sin duda, la utilización de software específico como acompañamiento en la construcción del aprendizaje matemático de los estudiantes es una de las grandes potencialidades de las TIC en el aula de matemáticas” (Ruiz, 2013, p. 21).

La importancia de los ambientes de aprendizaje basados en el uso de software de geometría dinámica radica en que estos activan el trabajo de los estudiantes en el estudio de diferentes objetos geométricos. En los medios digitales, las representaciones gozan de propiedades que no se tienen en el papel: son representaciones ejecutables. Evidentemente, el papel no revela la riqueza inherente al medio dinámico (Moreno & Ramírez, 2017). También es importante destacar que en los ambientes de geometría dinámica, los estudiantes pueden “visualizar, manipular y explorar objetos matemáticos que con el uso de lápiz y papel sería prácticamente imposible de realizar, además optimiza el tiempo de la misma, porque las construcciones geométricas se realizarían en poco tiempo y de forma precisa” (Miranda, 2011, p. 30).

En la investigación se abordaron las dificultades en el uso de los sistemas semióticos de representación y la formalización de conceptos matemáticos que presentan los estudiantes al trabajar la geometría euclidiana plana, particularmente lo referido a rectas y puntos notables del triángulo. Se tuvo en cuenta una estrategia basada en el aprendizaje por descubrimiento, para afrontar las dificultades de los estudiantes en el uso de los diversos tipos de lenguaje, como el natural, el gráfico y el simbólico, en el trabajo con triángulos y sus elementos notables, en especial con el estudio de sus propiedades y relaciones. Se propició que los estudiantes conjeturaran hacia la formalización de objetos geométricos, a partir de la exploración de un ambiente de geometría dinámica. Se pretendió plasmar estas ideas en un material virtual sobre el aprendizaje de los objetos notables del triángulo, diseñado e implementado por los investigadores en el aula de clase, para analizar la evolución en el aprendizaje y el desarrollo de los procesos del pensamiento espacial de los estudiantes.

Aspectos teóricos

En el aprendizaje de la geometría es importante que los estudiantes utilicen distintos sistemas de representación (Duval, 2016), por medio de los cuales puedan conceptualizar de mejor manera los diferentes objetos geométricos involucrados en las actividades de aprendizaje de la geometría de triángulos. Los ambientes de geometría dinámica permitieron una adecuada visualización y reconocimiento de figuras bidimensionales, ya que posibilitan usar herramientas primitivas de arrastres, rotaciones, traslaciones, entre otras. Esto permitió estudiar a profundidad los objetos geométricos involucrados en las prácticas de aula implementadas. A partir de los significados personales de los estudiantes, dichas mediaciones propiciaron el desarrollo de problemas geométricos específicos, para lograr una institucionalización de significados. El potencial semiótico de una herramienta usada para la enseñanza puede adecuarse y encaminarse hacia el desarrollo de procesos matemáticos. Mediante el análisis de las cualidades y restricciones, esta herramienta puede convertirse en un buen instrumento para el aprendizaje (Bartolini-Bussi & Mariotti, citados por Camargo et al., 2013).

En el desarrollo de esta investigación, se usó una metodología centrada en el aprendizaje por descubrimiento planteado por (Bruner, 1966), enfocada en un aprendizaje personalizado, a partir de la exploración y apropiación de situaciones concretas en ambientes de geometría dinámica, relacionados con las rectas y puntos notables del triángulo. Se buscó que los estudiantes conjeturaran propiedades y formalizaran conceptos sobre el triángulo en geometría euclidiana plana, a partir de la exploración de estos ambientes. En el aprendizaje por descubrimiento, “el instructor debe motivar a los estudiantes para que sean ellos mismos los que descubran relaciones entre conceptos y construyan conocimientos” (Guilar, 2009, p. 238).

En el trabajo de García (2010), se menciona que de la obra de Bruner (1960) emergen cuatro temas claves en el proceso educativo: “el papel central de la estructura en la enseñanza y el aprendizaje, la disposición, los pensamientos intuitivo y analítico, y la motivación” (p. 44). Estos elementos son importantes en el proceso de aprendizaje y, por lo tanto, deben tenerse en cuenta al diseñar y evaluar las tareas matemáticas propuestas para los estudiantes, con el fin de lograr aprendizajes más sólidos.

Actividad demostrativa en geometría.

En el trabajo de Camargo (2010) se explica la actividad demostrativa en geometría. Busca una aproximación conceptual a los procesos de explorar, conjeturar, definir y argumentar, los cuales están implícitos en dicha actividad. En esta investigación, se enfatizó en el desarrollo del pensamiento intuitivo y la visualización, que están implícitos en el trabajo heurístico que los estudiantes realizaron en el desarrollo de las tareas.

En la investigación se tuvieron en cuenta las siguientes etapas: exploración, conjeturación, argumentación y formalización de nociones y propiedades acerca de los puntos y rectas notables del triángulo, las cuales se analizaron a partir del trabajo realizado por el estudiante en la aplicación de los ambientes de aprendizaje. Se tomaron como base las nociones de explorar (Arsac; Arzarello; citados por Camargo, 2010, p. 50), conjeturar (Camargo, 2010, p. 51), definir (Camargo, 2010, p. 52), argumentar (Bartolini et al.; Duval; citados por Camargo, 2010, p. 52) y figuras y representaciones geométricas (Laborde; Mariotti; citados por Camargo 2010, p. 50). De esta manera, puede decirse que en geometría la exploración y el desarrollo de la intuición son fundamentales para la formulación de conjeturas y formalización de nociones y propiedades sobre diferentes objetos geométricos.

Geometría escolar.

El trabajo realizado en geometría por los estudiantes durante su etapa escolar puede describirse de acuerdo con lo planteado por Acosta y Fiallo (2017), quienes consideran cuatro etapas de la geometría escolar: geometría de las formas, geometría de las construcciones, geometría de las justificaciones y geometría de las demostraciones. En este estudio, se pudo analizar hasta la tercera etapa. El trabajo de los estudiantes se enfocó en la exploración heurística de los ambientes de geometría dinámica propuestos, con el fin de generar deducciones respecto a nociones y propiedades de los objetos geométricos contenidos en los ambientes. En este sentido, los procesos de exploración y justificación son fases cruciales en el aprendizaje de la geometría (Barbosa, 2013).

Acerca de GeoGebra.

De acuerdo con la experiencia de trabajo, el software GeoGebra ha sido de gran ayuda para aprender geometría, ya que permite explorar los objetos geométricos de una manera más versátil. De este modo, los estudiantes pueden hacer conjeturas sobre las propiedades de dichos objetos. Al ser un software interactivo y libre, presenta muchas ventajas para realizar cálculos algebraicos y aritméticos y generar construcciones geométricas interactivas y dinámicas (Carrillo, citado por Ruiz, 2013, p. 28).

Tareas matemáticas propuestas a los estudiantes.

Para el desarrollo de esta investigación, las tareas que se plantearon a los estudiantes se centraron en la exploración de ambientes de geometría dinámica, en los cuales se sugirieron algunas preguntas orientadoras, con el objetivo de encaminarlos a la formulación de conjeturas sobre nociones y propiedades de objetos geométricos relativos al triángulo. En cuanto a la actividad y tarea matemática, Ponte (2004) comenta que “principalmente, los alumnos obtienen el aprendizaje a partir de los factores clave: la actividad que realizan y la reflexión que efectúan al respecto”. En este sentido, una tarea es el objetivo de la actividad a realizar. Según este autor, las tareas matemáticas pueden clasificarse según el grado de dificultad y de apertura, la duración y el contexto. Para el caso de esta investigación, se propusieron tareas de exploración sobre los elementos notables del triángulo, clasificadas así: de tipo descriptivo, de formulación y validación de conjeturas, de nombramiento y caracterización, y finalmente las fundamentadas en la formulación de proposiciones.

Aspectos metodológicos

Para el desarrollo de la investigación, se escogió como unidad de análisis un grupo de 32 estudiantes de grado décimo de un colegio de Tunja, con edades entre ١٤ y ١٧ años. La recolección de la información se realizó a través de instrumentos como: prueba diagnóstica, cuestionarios, archivos digitales y análisis de las comunicaciones escritas hechas por los estudiantes al conjeturar y formalizar conceptos y propiedades geométricas del triángulo. Para la organización de la información, se nombraron los estudiantes como E1, E2, E3, y así sucesivamente.

El enfoque de investigación fue cualitativo, de tipo descriptivo-interpretativo. Se buscó describir y analizar de qué manera los estudiantes conjeturan y formalizan conceptos y propiedades relativos a las rectas y puntos notables del triángulo en geometría euclidiana plana. Para Fiorentini y Lorenzato (2010), en una investigación descriptiva, “el investigador desea describir o caracterizar con detalles una situación, un fenómeno o un problema. Generalmente este tipo de investigación utiliza observación sistemática (no etnográfica) o la aplicación de cuestionarios estandarizados, a partir de categorías previamente definidas” (p. 43).

Para el desarrollo de la investigación se usaron cinco ambientes virtuales, diseñados en el programa GeoGebra. El primer ambiente virtual se usó como prueba diagnóstica. Se les solicitó a los estudiantes explorar la herramienta con el fin de formular conjeturas y descubrir propiedades relativas al triángulo. En los demás ambientes se enfatizó en las rectas y puntos notables del triángulo. El orden en que se presentó a los estudiantes cada ambiente fue: medianas y baricentro; alturas y ortocentro; bisectrices e incentro; mediatrices y circuncentro. En estos ambientes virtuales se formularon preguntas orientadoras enfocadas en que los estudiantes descubrieran propiedades, formularan conjeturas y, finalmente, formalizaran nociones y propiedades de las rectas y puntos notables del triángulo en los que enfatizaba cada uno de los ambientes.

Para el análisis de la información, se establecieron categorías sobre el pensamiento espacial y el aprendizaje heurístico. En cuanto al pensamiento espacial, se analizaron elementos como la ubicación espacial, movimientos geométricos, procedimientos de construcción y determinación de invariantes. Para el caso del aprendizaje heurístico, se analizaron los procesos de conjeturación sobre nociones y propiedades del triángulo y el uso de lenguaje natural, lenguaje simbólico y lenguaje matemático, en el proceso de formulación y validación de conjeturas sobre los elementos notables del triángulo.

Análisis de resultados

Se realizó un análisis descriptivo-interpretativo de la información recolectada en la prueba diagnóstica y en los ambientes virtuales. Para el análisis, se procesó la información en una versión de prueba del programa Atlas.ti. Se transcribieron las respuestas de los estudiantes, se hizo la categorización y finalmente se elaboraron y organizaron las redes respecto a cada una de las rectas y puntos notables del triángulo. Se adoptó la caracterización y forma de análisis de datos en este programa descritas por Vargas, González y Llinares (2011, p. 189).

La prueba diagnóstica se hizo con el fin de identificar dificultades de los estudiantes al estudiar las propiedades del triángulo en geometría plana, a partir de la exploración de un ambiente de geometría dinámica denominado Animación de triángulos en GeoGebra. La figura 1 es una imagen de la pantalla principal de dicho ambiente. Allí los estudiantes podían explorar los diferentes triángulos que se formaban y hacer una clasificación, de acuerdo con la medida de sus ángulos y de sus lados. Los diversos triángulos se podían visualizar al mover los deslizadores de forma manual o mediante la reproducción automática, herramientas con las que cuenta el programa.

Cada estudiante exploró de forma individual el ambiente en un computador. La sesión fue de dos horas. En el ambiente había un cuestionario de diagnóstico que los estudiantes podían responder a medida que realizaban la exploración. Para esto, se les suministró una hoja de papel para responder por escrito las preguntas.

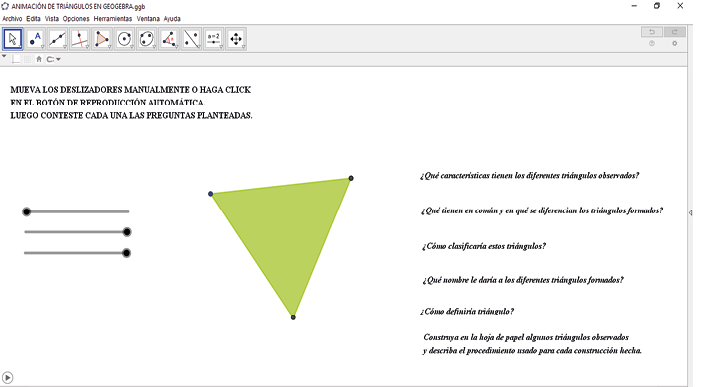
Figura 1. Ambiente de geometría dinámica aplicado para la prueba diagnóstica. Fuente: elaboración propia.

Tabla 1
Cuestionario de la prueba diagnóstica.

Tarea matemática de exploración

Explora el recurso dado —animación de triángulos en GeoGebra—. A partir de la exploración y observación realizada, responde las siguientes preguntas: ¿Qué características tienen los diferentes triángulos observados? ¿Qué tienen en común y en qué se diferencian los triángulos formados? ¿Cómo clasificaría estos triángulos? ¿Qué nombre le daría a los diferentes triángulos explorados? ¿Cómo definiría triángulo? Construya en la hoja de papel algunos triángulos observados y describa el procedimiento usado para cada construcción.

Fuente: elaboración propia.

De acuerdo con las tareas matemáticas descritas en la sección anterior, se propuso a los estudiantes una tarea de exploración, de duración corta y en el contexto de las matemáticas. Previamente, los estudiantes habían tenido experiencia en la realización de construcciones con regla y compás de diferentes figuras geométricas, en particular de triángulos. En la tabla 1, se muestran las preguntas orientadoras que estaban en el ambiente, por medio de las cuales se buscaba identificar conocimientos de los estudiantes acerca de las propiedades del triángulo y su clasificación según la medida de sus lados y de sus ángulos. También se buscaba un acercamiento a su noción de triángulo.

A continuacion se muestran algunas descripciones hechas por los estudiantes respecto a la caracterización, clasificación y noción de triángulo.

En relación con la caracterizacion de triángulos.

• “Así cambien sus ángulos internos, de cualquier manera la suma de estos tendrá que dar 180º”.
• “Su base no siempre es horizontal”.

Respecto a la clasificación y nombramiento de los triángulos.

• “Se clasifican de acuerdo con las medidas de los lados y de los ángulos”.

Equilátero: todos sus lados son iguales.

Isósceles: dos de sus lados son iguales.

Escaleno: todos sus lados desiguales.

Acutángulo.

Rectángulo: tienen un ángulo de 90º.

Obtusángulo.

• “Se clasificarían por simétricos y asimétricos: isósceles, equilátero, escaleno, rectángulo”.
• “Por sus ángulos, por sus lados, por su clase, por su forma”.

En relación con la noción de triángulo.

• “Triángulo es una figura geométrica formada por tres lados, vértices y ángulos. Su forma puede ser variada dependiendo de la medida de sus lados sin que estos dejen de ser tres. Es la base de la trigonometría”.
• “Figura geométrica con tres lados —a, b, c— y tres vértices —A, B, C— que, de acuerdo con su clasificación, toman cierta medida formando ángulos de diferentes medidas”.
• “Es la unión de 3 puntos, la cual constituye una figura plana que se puede clasificar según la medida de sus ángulos y de sus lados. Además tienen como propiedad que la sumatoria de sus ángulos internos siempre será 180º”.
• “El triángulo es un polígono que posee tres lados y que van conectados entre sí, formando unos puntos llamados vértices, y sus lados pueden tener diferentes medidas”.
• “Figura geométrica formada por 3 rectas que se cortan y forman 3 ángulos”.
• “Figura de tres lados y tres vértices con ángulos internos y externos. Su medida puede variar y sus ángulos también. Se han usado como símbolo de muchas formas. En el triángulo también aplica un fractal”.

De acuerdo con las afirmaciones, se evidencia que al tratar de identificar características de los diferentes triángulos formados, los estudiantes describen algunos aspectos específicos y otros de manera muy superficial, según lo que observaron en la exploración del ambiente. Cuando afirman “la suma de los angulos internos es 180º”, la mayoría lo hace con mucha naturalidad, debido a que es una “ley de triángulos” en geometría euclidiana plana, que ha sido consolidada desde años atrás. Sin embargo, esto no sucede con otras propiedades del triángulo en geometría plana, que no pudieron identificar facilmente explorando el ambiente.

En relación con la clasificación y denominación de los triángulos en la exploración del ambiente de geometría dinámica, la mayoría de estudiantes identificó y describió correctamente que se clasifican de acuerdo con la medida de sus lados y de sus ángulos. Sin embargo, al definir los tipos de triángulos, se evidencian falencias en sus apreciaciones, debido a que hacen una descripción superficial con algunas características de los triángulos. Faltan más elementos para hacer una aproximacion más elaborada del tipo de triángulo que se quiere definir. De la misma manera, nombran algunos tipos de triángulo correctamente, pero no presentan su definición.

Ante esto, puede decirse que las afirmaciones de los estudiantes son limitadas, puesto que no se evidencia un estudio a profundidad de las propiedades que allí se pueden encontrar sobre los diferentes triángulos. Es decir, no es tan natural para los estudiantes formular conjeturas un poco más elaboradas, aun teniendo la posibilidad de explorar objetos geométricos de forma dinámica en el ambiente.

Del mismo modo, en cuanto a las nociones de triángulo de los estudiantes, es evidente que corresponden a la descripcion de características observadas en la representación gráfica de los diferentes triángulos, lo cual lleva a pensar en lo que Duval (1993, citado por D’Amore, Pinilla, Iori & Matteuzzi, 2015), llama la paradoja cognitiva, pues los estudiantes para elaborar una definición, describen lo que pueden observar en la representación inmediata que tienen del triángulo, pero añaden expresiones como “figura geométrica”, “forma geométrica” o “polígono”.

Respecto a las construcciones con regla y compás hechas por los estudiantes, se evidenció que han tenido poca experiencia en su manejo y tienden a realizar construcciones a mano alzada, lo cual genera poca concordancia entre lo descrito en un procedimiento y la respectiva construcción. Tal es el caso de un estudiante que realizó una construcción que se asemeja a la construcción con regla y compás de un triángulo equilátero, pero en el procedimiento descrito destaca que corresponde a un triángulo rectángulo.

A partir de estas consideraciones, se diseñaron y se aplicaron cuatro ambientes de geometría dinámica referentes a las rectas y puntos notables del triángulo. En cada uno se propusieron tareas de exploración, mediante las cuales se buscaba que los estudiantes formularan conjeturas en lenguaje natural y posteriormente formalizaran nociones y propiedades del triángulo.

Rectas y puntos notables del triángulo

Se diseñaron y se implementaron cuatro ambientes virtuales elaborados en GeoGebra, en los cuales los estudiantes exploraron de manera individual las rectas y puntos notables del triángulo, así como la circunferencia inscrita y circunscrita en el mismo. En estos ambientes, se incluyeron diferentes tareas y preguntas orientadoras que los estudiantes debían responder de manera individual y de forma escrita en una hoja de papel. Mediante estas tareas se buscó que los estudiantes formularan y validaran conjeturas con miras a una posterior formalización de nociones y propiedades del triángulo y de sus elementos notables.

Se buscó que ellos mismos descubrieran los términos geométricos más apropiados para denotar los elementos notables del triángulo, por ello se le dio el nombre inicialmente de punto y rectas notables tipo 1 —baricentro y medianas—, punto y rectas notables tipo 2 —ortocentro y alturas—, punto y rectas notables tipo 3 —incentro y bisectriz— y punto y rectas notables tipo 4 —circuncentro y mediatriz—. De la misma manera, para el caso de la circunferencia inscrita y circunscrita en el triángulo, inicialmente se nombraron como Circunferencia tipo 1 y Circunferencia tipo 2. No se usaron los nombres que usualmente se emplean para las rectas notables —mediana, altura, bisectriz, mediatriz—, ni para los puntos notables —baricentro, ortocentro, incentro y circuncentro—, ni de la circunferencia inscrita y circunferencia circunscrita, con el fin de propiciar el uso del lenguaje natural de los estudiantes y de que tuvieran la oportunidad de notarlos según sus concepciones.

Como resultado del análisis basado en la información procesada en Atlas.ti, se elaboraron redes en las que se destacan las respuestas más relevantes de los estudiantes frente a las tareas propuestas en los diferentes ambientes virtuales. En las redes se muestra una panorámica de la cantidad de respuestas y nociones de los estudiantes frente a las categorías de análisis. La organización de las redes se realizó de acuerdo a las respuestas de los estudiantes, las cuales se agruparon según los siguientes aspectos: elementos del triángulo, clasificación de triángulos y de ángulos, nombramiento y caracterización de las rectas y puntos notables, procedimientos de construcción de los elementos notables del triángulo, formulación de conjeturas y enunciado de propiedades.

Medianas y baricentro del triángulo

En el ambiente virtual 2, se hizo énfasis en las medianas y baricentro del triángulo —punto y rectas notables tipo 1—. Los estudiantes debían desarrollar varias tareas referentes a este tipo de punto y rectas notables, a partir de la exploración del ambiente virtual (figura 2).

La red construida en Atlas.ti con las respuestas de los estudiantes al implementar el ambiente virtual 2 (figura 3) describe los aspectos relevantes sobre las rectas notables tipo 1, que hacen referencia a las medianas del triángulo y su punto de intersección, baricentro. Aquí se buscó que los estudiantes exploraran el ambiente y descubrieran propiedades del triángulo al formular conjeturas, inicialmente con el uso del lenguaje natural, para después introducir las nociones geométricas de mediana y baricentro.

En la figura 2 se muestra una imagen del segundo ambiente virtual y las tareas de exploración propuestas en GeoGebra. La estructura es similar en los cuatro ambientes virtuales referentes a los elementos notables del triángulo.

Figura 2. Ambiente virtual 2: punto y rectas notales tipo 1, tareas propuestas. Fuente: elaboración propia.

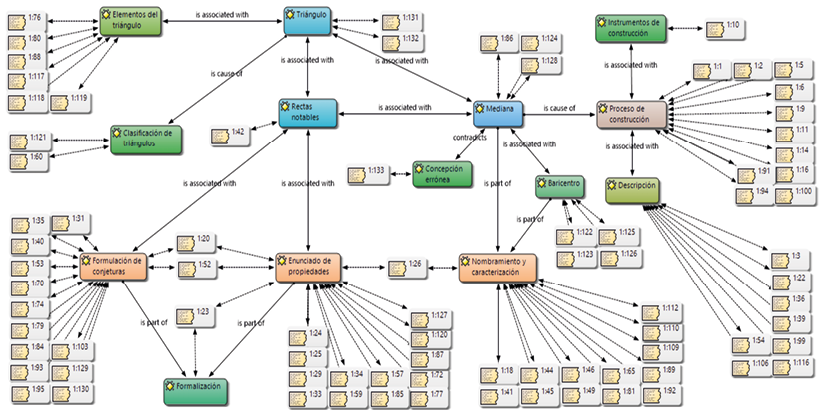
Figura 3. Red 1: medianas y baricentro del triángulo. Fuente: elaboración propia.

Primera actividad.

• Describa cómo se podría construir cada recta notable tipo 1, con respecto al vértice y lado del triángulo ABC por los cuales pasa. Si lo considera puede hacer una construcción en el anexo cuadriculado.

Alrededor de la mitad de los estudiantes identificó claramente la forma de construir dichas rectas, al reconocer los elementos propios de su construcción. Algunos estudiantes que no lo lograron hicieron énfasis en los instrumentos de construcción, como la regla y el compás, y no lograron identificar algún elemento como punto medio, vértice y demás elementos del triángulo.

Segunda pregunta.

• ¿Es posible que el punto de intersección de las rectas notables tipo 1 sea exterior al triángulo ABC o esté ubicado sobre alguno de sus vértices? Justifique su respuesta.

La mayoría de estudiantes afirmó que el punto de intersección de las rectas notables tipo 1 —medianas— siempre está al interior del triángulo. Algunos estudiantes destacaron que, si el punto de intersección de las rectas notables se hace coincidir con un vértice del triángulo, ya no se podrá visualizar un triángulo, sino una línea recta.

Tercera pregunta.

• ¿Qué nombre podrían recibir las rectas notables tipo 1 y su punto de intersección J?

Gran parte de los estudiantes utilizó términos como mediana y baricentro en las descripciones hechas por ellos. Se pretendía que pudieran hacer un nombramiento y caracterización de las rectas notables tipo 1 —medianas— y del punto notable —baricentro—, a partir de la exploración del ambiente y el desarrollo de las tareas.

Cuarta actividad.

• Formule en lenguaje natural algunas proposiciones que surjan de esta actividad.

Gran parte de los estudiantes formuló conjeturas y describió propiedades de las medianas y baricentro del triángulo. Algunos ejemplos de afirmaciones hechas por los estudiantes se evidencian en las figuras 4 y 5. La mayoría elaboró descripciones en las que se afirma que el punto de intersección —baricentro— de las rectas notables tipo 1 —medianas— siempre está al interior del triángulo, sin importar la longitud de sus lados, ni la amplitud de sus ángulos internos.

Figura 4. Respuestas de los estudiantes E17 y E4 en la tarea 4 del ambiente virtual 2.

Del mismo modo, un estudiante dijo que el punto de intersección corresponde al centro geométrico del triángulo. Esta afirmación se destaca como una de las propiedades del baricentro.

Alturas y ortocentro del triángulo

El ambiente virtual 3 hizo referencia a las rectas y punto notables tipo 2 —alturas y ortocentro— del triángulo. Había cuatro tareas de exploración que los estudiantes debían desarrollar de forma individual, al registrar en una hoja de papel las respuestas.

Figura 5. Respuestas de los estudiantes E19 y E23 en la tarea 4 del ambiente virtual 2.

En la figura 6, se muestra la red construida en Atlas.ti a partir de las respuestas de los estudiantes en el ambiente virtual 3. Se buscó que formularan conjeturas, inicialmente en lenguaje natural, y posteriormente con nociones geométricas de altura y ortocentro del triángulo.

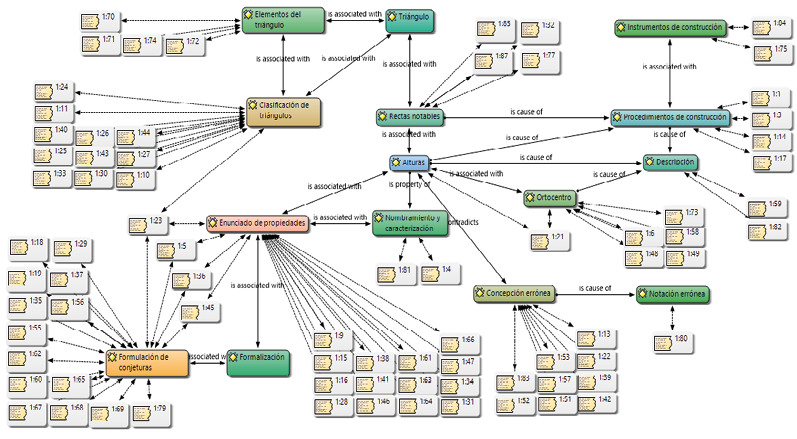
Figura 6. Red 2: Alturas y ortocentro del triángulo. Fuente: elaboración propia.

Primera actividad.

• Describa cómo se podría construir cada recta notable tipo 2, respecto al vértice y lado del triángulo ABC por los cuales pasa. Si lo considera, puede hacer una construcción en el anexo cuadriculado.

En cuanto a la descripción de la forma como podrían construirse las rectas notables tipo 3 —alturas—, no todos los estudiantes pudieron describir un procedimiento que permitiera dicha construcción. Algunos hicieron referencia a las características de la figura observada por medio de la exploración. Aquellos que lograron describir un procedimiento, identificaron elementos del triángulo, como lados, ángulos y vértices. Del mismo modo, nombraron instrumentos, como la regla y el compás, como elementos esenciales en la elaboración de dichas construcciones.

Segunda pregunta.

• ¿Qué tipo de triángulo ABC se forma cuando el punto de intersección de las rectas notables tipo 2 es al interior del triángulo, es exterior al triángulo, o está ubicado sobre uno de los vértices del triángulo?

La mayoría describió una clasificación de los triángulos, según la medida de sus lados y la amplitud de sus ángulos internos. Mencionaron los triángulos equilátero, isósceles escaleno, rectángulo, obtusángulo y acutángulo. En algunos casos explicaron el porqué del nombre asignado a estos.

Tercera pregunta.

• ¿Qué nombre podrían recibir las rectas notables tipo 2 y su punto de intersección D?

Pocos estudiantes utilizaron nociones geométricas de altura y ortocentro para referirse a las rectas y punto notables presentadas en el ambiente virtual.

Cuarta actividad.

• Formule en lenguaje natural algunas proposiciones que surjan de esta actividad.

De los 32 estudiantes, 28 pudieron formular conjeturas y describir propiedades del triángulo, al usar nociones geométricas de altura y ortocentro. Algunas afirmaciones de los estudiantes se evidencian en las figuras 7 y 8. Aproximadamente 16 estudiantes pudieron formular conjeturas sobra la construcción de las alturas del triángulo y sobre la relación de estas con los elementos del triángulo.

Figura 7. Respuestas de los estudiantes E4, E6 y E9 en la tarea 4 del ambiente virtual 3.

Figura 8. Respuestas del estudiante E23 en la tarea 4 del ambiente virtual 3.

Bisectrices e incentro del triángulo

El ambiente virtual 4 hizo referencia a las rectas notables tipo 3 —bisectrices—, su punto de intersección —incentro— y la circunferencia tipo 1 —circunferencia inscrita—. Constaba de una tarea de exploración en la que cada estudiante de forma individual debía desarrollar cuatro actividades acerca de estas rectas y punto notables del triángulo. En la figura 9 se muestra la red construida en Atlas.ti a partir de las respuestas de los estudiantes.

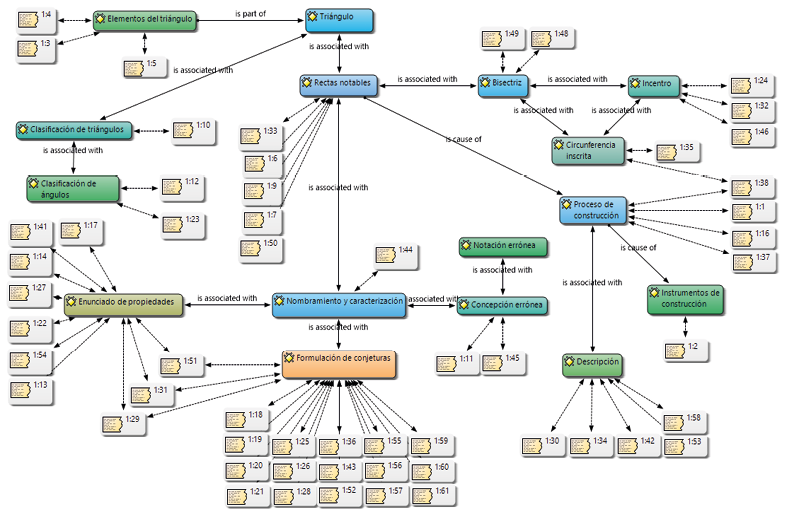
Figura 9. Red 3: bisectrices e incentro del triángulo. Fuente: elaboración propia.

Primera actividad.

• Describa cómo se podría construir cada recta notable tipo 3, con respecto al vértice y lado del triángulo ABC1 por los cuales pasa. Si lo considera puede hacer una construcción en el anexo cuadriculado.

Solamente 9 de los 32 estudiantes pudieron describir un procedimiento mediante el cual se podrían construir las rectas notables tipo 3 —bisectrices— y la forma como estas se relacionan con los lados y vértices del triángulo. También nombraron instrumentos, como la regla y el compás, como elementos necesarios en la elaboración de este tipo de construcciones.

Segunda pregunta.

• ¿Es posible que el punto de intersección de las rectas notables tipo 3 sea exterior al triángulo ABC? ¿Puede estar ubicado sobre alguno de sus lados o alguno de sus vértices? Justifique su respuesta.

Aproximadamente un 90% de los estudiantes hizo afirmaciones respecto a que el punto de intersección —incentro— no puede ser exterior al triángulo, debido a que la construcción de las bisectrices, implica que el punto donde se intersectan estas tres rectas siempre esté en el interior del triángulo.

Un 15% de los estudiantes afirmó que si el punto de intersección coincide con uno de los vértices del triángulo, entonces la forma triangular desaparece y se transforma en una línea recta, debido a que dicho punto quedaría en relación colineal con los otros dos vértices del triángulo, y por lo tanto, no podría ser exterior al triángulo. De la misma manera, un estudiante afirmó que, debido a que la circunferencia está inscrita en el triángulo y a que el punto de intersección de las mediatrices es el centro de dicha circunferencia, dicho punto siempre está al interior del triángulo, independientemente de la variación en la medida de sus lados y amplitud de sus ángulos internos.

Tercera pregunta.

• Describa cómo se podría construir la circunferencia tipo 1. ¿Qué relación existe entre esta circunferencia y el triángulo ABC?

Treinta estudiantes describieron algún procedimiento general de construcción de dicha circunferencia, sin tener en cuenta nociones formales en sus descripciones. De la misma manera, un 70% de los estudiantes afirmó que la circunferencia debe intersecar en un solo punto a cada uno de los lados del triángulo; de lo contrario, significa que está construida incorrectamente y que, independientemente de las modificaciones que se hagan al triángulo, la circunferencia siempre es interior.

Cuarta pregunta.

• ¿Qué nombre podría recibir cada uno de los siguientes objetos: las rectas notables tipo 3, punto de intersección de estas rectas, la circunferencia tipo 1?

Un 60% de los estudiantes nombró correctamente las bisectrices e incentro del triángulo en las descripciones. Los demás trataron de definir dichos objetos geométricos a partir de sus características y, en algunos casos, con concepciones erróneas para nombrar y caracterizar dichos objetos. En el caso de la circunferencia inscrita, un 70% la nombró correctamente y describió sus características. El porcentaje que no nombró correctamente la circunferencia tipo 1 utilizó en su descripción términos como “circunferencia base” o “círculo”.

Quinta actividad

• Formule en lenguaje natural algunas proposiciones que surjan de esta actividad.

Un 75% formuló conjeturas sobre la construcción de las bisectrices e incentro del triángulo y de la circunferencia inscrita, y respecto a las relaciones entre estos objetos geométricos y los elementos propios del triángulo. En relación con la caracterización de las bisectrices y del incentro del triángulo, hubo afirmaciones tales como: “las rectas siempre van a permanecer dentro del triángulo”; “el punto de intersección de las bisectrices nunca es exterior al triángulo”; y “el incentro nunca va a salir del triángulo”. Otros ejemplos de conjeturas se muestran en la figura 10. Aunque no se evidencia una definición formal, dichas afirmaciones se encaminan hacia la caracterización de nociones y propiedades de las rectas y punto notables presentadas en este ambiente virtual.

Figura 10. Respuestas de los estudiantes E4, E13 y E17 en la tarea 5 del ambiente virtual 4.

En relación con la circunferencia inscrita, se toman algunos ejemplos de afirmaciones hechas por los estudiantes tales como: “los vértices casi nunca tocan la circunferencia”, “la circunferencia va siempre dentro del triángulo”; “si la circunferencia no toca los tres lados del triángulo, está mal construida”; “la circunferencia pasa por el punto medio de los lados en un triángulo equilátero”; y “si el triángulo es equilátero, las rectas notables dividen en seis partes iguales la circunferencia”. Se detecta un proceso de conjeturación en donde se utilizan nociones relativas a los elementos del triángulo y su clasificación. Esto permite el descubrimiento de relaciones entre estos objetos geométricos, lo cual facilita el proceso de formalización de nociones y propiedades de las bisectrices e incentro del triángulo, así como de la circunferencia inscrita en el mismo.

Mediatrices y circuncentro del triángulo

El quinto ambiente virtual hace referencia a las rectas notables tipo 4 —mediatrices—, su punto de intersección —circuncentro— y la circunferencia tipo 1 —circunferencia circunscrita—. Se presentó a los estudiantes una tarea de exploración, en la que respondieron individualmente preguntas relacionadas con estas rectas y un punto notable del triángulo. En la figura 11 se muestra la red construida en Atlas.ti con las respuestas de los estudiantes.

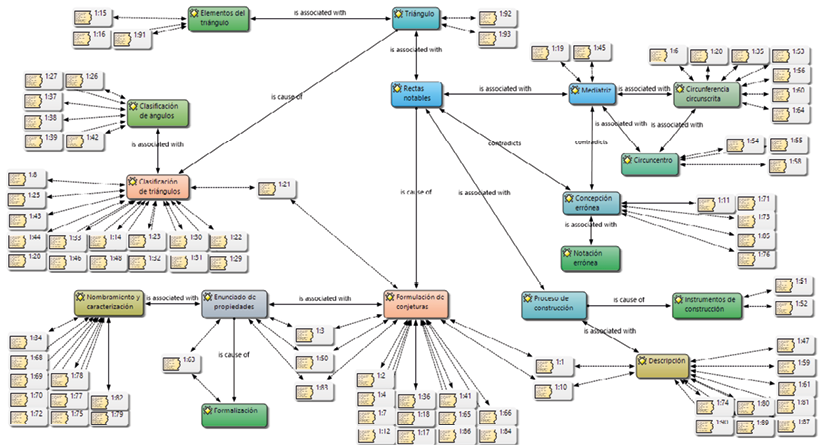
Figura 11. Red 4: mediatrices y baricentro del triángulo. Fuente: elaboración propia.

Primera actividad.

• Establezca relaciones entre las rectas notables tipo 4 y los lados del triángulo ABC.

Solamente un 20% estableció con facilidad relaciones entre las rectas y los lados del triángulo. No fue natural para ellos identificar la perpendicularidad de las rectas notables —mediatrices— con el lado respectivo del triángulo por el cual pasa, que además intersecta su punto medio.

Segunda pregunta.

• ¿Qué condiciones se deben tener en el triángulo ABC para que el punto de intersección de las rectas notables tipo 4 esté ubicado: al interior del triángulo, al exterior del triángulo, sobre uno de los lados del triángulo? Especifique en cada caso el tipo de triángulo que se forma.

Un 90% de los estudiantes, a partir de la exploración y modificación del triángulo, pudo clasificar los diversos triángulos resultantes de acuerdo con la medida de sus lados y la amplitud de sus ángulos internos. En las diferentes descripciones nombraron triángulos equiláteros, escalenos, isósceles, acutángulos, rectángulos y obtusángulos. Describieron las condiciones del triángulo para los casos en cuestión. Identificaron que: para que el punto de intersección —circuncentro— quede ubicado en el interior del triángulo, este debe ser acutángulo; para que sea exterior al triángulo, debe ser obtusángulo; y para que esté ubicado en uno de los lados del triángulo, debe ser rectángulo.

Tercera pregunta.

• Describa cómo se podría construir la circunferencia tipo 2. ¿Qué relación existe entre esta circunferencia y el triángulo ABC? Si lo considera, puede hacer una construcción en el anexo cuadriculado.

Los estudiantes elaboraron descripciones de cómo se podría construir la circunferencia tipo 1 —circunferencia circunscrita—, en las que destacaron que a partir del punto de intersección —circuncentro— de las rectas notables tipo 4 —mediatrices—, se toma como centro de la circunferencia y se traza de tal manera que esta pase por los tres vértices del triángulo.

Cuarta pregunta.

• ¿Qué nombre podrían recibir los siguientes objetos: las rectas notables tipo 4, el punto de intersección de estas rectas, la circunferencia tipo 2?

Los estudiantes hicieron descripciones en las cuales usaron nociones geométricas de las mediatrices y circuncentro del triángulo, e hicieron referencia a las rectas notables tipo 4 y su punto de intersección respectivamente. Del mismo modo, aproximadamente el 50% nombró correctamente la circunferencia circunscrita y la caracterizó.

Quinta actividad.

• Formule en lenguaje natural algunas proposiciones que surjan de esta actividad.

Aproximadamente un 60% formuló conjeturas en lenguaje natural sobre las mediatrices y circuncentro del triángulo. Formularon propiedades del triángulo en relación con estas rectas y punto notables, y con la circunferencia circunscrita. Algunas descripciones de los estudiantes hicieron referencia a que, en este caso, el punto de intersección de las rectas notables puede estar ubicado sobre uno de los lados del triángulo, interior o en el exterior del mismo. Destacaron que el incentro es el centro de la circunferencia circunscrita, que además contiene al triángulo. De la misma manera, hicieron afirmaciones respecto a que, sin importar las dimensiones del triángulo, la circunferencia siempre va a pasar por los tres vértices de dicho triángulo y, del mismo modo, si el triángulo cambia su área, entonces el área de la circunferencia también cambiará.

Conclusiones

La exploración de objetos geométricos mediante el uso de ambientes de geometría dinámica facilitó a los estudiantes el desarrollo de los procesos de formulación y validación de conjeturas, así como el descubrimiento de propiedades de los objetos que se están estudiando. Esto propicia el trabajo heurístico de los estudiantes y permite una mayor consolidación de sus aprendizajes.

Cerca del 80% realizó correctamente una clasificación de los triángulos, de acuerdo con la medida de sus lados y la amplitud de sus ángulos internos. Hicieron descripciones en las que caracterizaron los diferentes tipos de triángulos y los nombraron de forma correcta.

En cuanto a la construcción de las rectas y puntos notables, los estudiantes describieron adecuadamente procedimientos, en donde se nombran elementos con los cuales se pueden elaborar dichas construcciones.

Aproximadamente el 80% de los estudiantes formuló conjeturas sobre la construcción de las rectas notables del triángulo, la circunferencia inscrita y la circunferencia circunscrita. Pudieron formular conjeturas acerca de las relaciones entre los diversos triángulos explorados en los ambientes virtuales y las rectas y puntos notables, y con la circunferencia inscrita y circunscrita.

Se percibió un progreso adecuado en el pensamiento intuitivo de los estudiantes al implementar las actividades propuestas, basadas en la visualización de los sistemas de representación de puntos, rectas y circunferencias notables del triángulo, mediadas con ambientes dinámicos elaborados en GeoGebra.

Refencias

Acosta, M., & Fiallo, J. (2017). Enseñando geometría con tecnología digital: una propuesta desde la teoría de las situaciones didácticas. Bogotá: Universidad Distrital Francisco José de Caldas.

Barboza, J. (2013). Explorar y descubrir para conceptualizar en geometría. Scientia et Technica, 18(2). Recuperado de http://www.redalyc.org/articulo.oa?id=849/84929153012

Boude, Ó., & Cárdenas, M. (2016). Cómo empoderar a las instituciones de educación básica en la incorporación de las TIC. Revista Academia & Virtualidad, 9(2), 27-40. https://doi.org/http://dx.doi.org/10.18359/ravi.1862

Bruner, J. S. (1966). Toward a theory of instruction (Vol. ٥٩). Harvard University Press.

Camargo, L. (٢٠١٠). Descripción y análisis de un caso de enseñanza y aprendizaje de la demostración en una comunidad de práctica de futuros profesores de matemáticas de educación secundaria (Tesis doctoral, Universidad de Valencia, Valencia, España).

Camargo, L., & Acosta, M. (2012). La geometría, su enseñanza y su aprendizaje. Tecné, Episteme y Didaxis - TED, (32), 4-8. Recuperado de http://www.scielo.org.co/scielo.php?script=sci_arttext&pid=S0121-38142012000200001&lng=en&tlng=es

Camargo, L., Pérez, C., Plazas, T., Perry, P., Samper, C., & Molina, Ó. (2013). Enseñanza de la geometría mediada por artefactos: teoría de la mediación semiótica. En P. Perry (Ed.), Memorias del 21º Encuentro de geometría y sus aplicaciones (pp. 85-96). Bogotá, Colombia: Universidad Pedagógica Nacional.

Correa, J., & Pablos, J. (2009). Nuevas tecnologías e innovación educativa. Revista de Psicodidáctica, 14(1), 133-145.

D’Amore, B., Pinilla, M. F., Iori, M., & Matteuzzi, M. (2015). Análisis de los antecedentes histórico-filosóficos de la “Paradoja cognitiva de Duval”. Revista latinoamericana de investigación en matemática educativa, 18(2), 177-212.

Duval, R. (2016). Las condiciones cognitivas del aprendizaje de la geometría. Desarrollo de la visualización, diferenciaciones de los razonamientos, coordinación de sus funcionamientos. En R. Duval, & A. Sáenz, Comprensión y aprendizaje en matemáticas: perspectivas semióticas seleccionadas (pp. 13-60). Bogotá: Editorial Universidad Distrital Francisco José de Caldas.

Fandos, M., Jiménez, J., & González, A. (2002). Estrategias didácticas en el uso de las Tecnologías de la Información y la Comunicación. Acción Pedagógica, 11(1), 28-39. Recuperado de http://www.comunidadandina.org/bda/docs/VE-EDU-0003.pdf

Fiorentini, D., & Lorenzato, S. (2010). Investigación en educación matemática: recorridos históricos y metodológicos (Trad. A. Jiménez). Campinas, SP: Autores Asociados Ltda.

Gamboa R., & Ballesteros, E. (2009). Algunas reflexiones sobre la didáctica de la geometría. Cuadernos de investigación y formación en educación matemática, 4(5), p. 113-136.

García, E. (2010). Pedagogía constructivista y competencias: lo que los maestros necesitan saber. México: Trillas.

Guilar, M. (2009). Las ideas de Bruner: “de la revolución cognitiva” a la “revolución cultural”. Educere, 13(44), 235-241. Recuperado de http://www.redalyc.org/articulo.oa?id=356/35614571028

Gutiérrez, A. (2011). Reflexiones sobre la enseñanza de la geometría en los niveles de primaria y secundaria. En P. Perry (Ed.), Memorias 20° Encuentro de geometría y sus aplicaciones (pp. 3-14). Bogotá: Universidad Pedagógica Nacional.

Miranda, N. (2011). Caracterización del uso de las TIC en la enseñanza de los puntos notables de los triángulos. Medellín: Universidad Nacional de Colombia.

Moreno, L., & Ramírez, R. (2017). La geometría al encuentro del aprendizaje. Educación Matemática, 29(1), 9-36. https://doi.org/10.24844/EM2901.01.

Ponte, J. (2004). Problemas e investigaciones en la actividad matemática de los alumnos. En J. Giménez, L. Santos, & J. Ponte (Eds.), La actividad matemática en el aula (pp. 25-34). Barcelona: Graó.

Ruiz, J. (2013). Las TIC en la enseñanza y aprendizaje de las matemáticas. Bogotá: Ediciones de la U.

Samper, C., & Toro, J. (2017). Un experimento de enseñanza en grado octavo sobre la argumentación en un ambiente de geometría dinámica. Revista Virtual Universidad Católica del Norte, (50). Recuperado de http://www.redalyc.org/articulo.oa?id=1942/194250865020.

Vargas J., González M.T., Llinares, S. (2011). Atlas TI como herramienta de análisis de la práctica docente: el caso de la función exponencial. En M.M. Moreno, N. Climent (Eds.), Investigación en Educación Matemática. Comunicaciones de los grupos de investigación de la SEIEM (pp. 187-199). Lleida.

---