En la industria existen diferentes métodos de generación de energía, entre los cuales podemos encontrar termoeléctricas y plantas nucleares. Los más amigables con el medio ambiente generan electricidad a partir de recursos renovables y casi inagotables, como la energía solar fotovoltaica y la energía eólica.
En la generación de energía con viento, existen dos tipos grandes de rotores y se pueden clasificar según su orientación, de eje horizontal que es el más conocido y de eje vertical. Los aerogeneradores de eje vertical, también conocidos como VAWT, Vertical Axis Wind Turbines […] fueron de las primeras máquinas que se utilizaron para la captación de energía eólica. Su principal característica es que el eje de rotación se encuentra en posición perpendicular al suelo y a la dirección del viento. (Busquets, 2013, p. 33)
El desarrollo de un modelo de rotor de eje vertical tipo Darrieus se lleva a cabo con base en la teoría de modelos. El modelo representa una réplica a escala de un prototipo. Un prototipo es un equipo a escala real 1:1. La teoría de modelos permite realizar pruebas de laboratorio con el modelo para obtener resultados cercanos y altamente fiables con respecto a lo que se mediría si se trabaja en campo con un prototipo.
El análisis dimensional es un método para verificar ecuaciones y planificar experimentos sistemáticos. A partir del análisis dimensional, se obtiene una serie de grupos adimensionales, que van a permitir utilizar los resultados experimentales obtenidos en condiciones limitadas, a situaciones en que se tengan diferentes dimensiones geométricas, cinemáticas y dinámicas; y muchas veces en casos en que las propiedades del fluido y del flujo son distintas de las que se tuvieron durante los experimentos. (Escuela Politécnica Superior de Ingeniería de Gijón Ingenieros Industriales, s. f.)
Esto, por un lado, permite reducir costos en equipo y personal para realizar pruebas en campo. Por otra parte, permite hacer cambios en el experimento, a partir del estudio de nuevos fenómenos o de fenómenos con poca documentación científica.
Para lograr el objetivo de este estudio, la teoría de modelos indica que mediante el teorema de Π de Buckingham se pueden determinar parámetros que gobiernan el desarrollo del modelo, al establecer relaciones de semejanza entre el prototipo y el modelo. Si se cumplen dichas relaciones, se obtienen mediciones fiables. Las relaciones de semejanza pueden ser: relación de semejanza dinámica, relación de semejanza cinemática y relación de semejanza geométrica.
Las relaciones de semejanza se emplean para el trabajo con modelos a escala en túneles aerodinámicos con el objetivo de que el comportamiento de los mismos sea lo más cercano posible a como se comportaría en una situación real el objeto en cuestión y poder extrapolar resultados. (Sánchez, 2017, p. 24)
En el presente trabajo se hizo uso de la semejanza dinámica y de la geométrica, lo cual se muestra con más detalle en la metodología. Para realizar la medición y el estudio del modelo desarrollado, se diseñó una estación de trabajo ―banco eólico de eje vertical― para garantizar las condiciones de flujo y, de este modo, variar dichas condiciones sobre el rotor. De la misma manera, el modelo de rotor obtenido se diseñó para permitir su remplazo por otro con características geométricas diferentes. El desarrollo del diseño del banco permite el reconocimiento de variables geométricas y de flujo sobre el desempeño del modelo de rotor de eje vertical. En este documento se desarrolla el objetivo de crear el modelo CAD y establecer parámetros de flujo y parámetros geométricos.
Para resolver problemas con el teorema de Π de Buckingham, se mencionan y se enlistan las características del problema: geométricas, dinámicas, del fluido, entre otras. Estos grupos contienen magnitudes físicas. Piden ciertos parámetros que se denotan como n, j y k, definidos como número de magnitudes físicas, parámetros repetitivos y parámetros adimensionales, respectivamente.
Metodología
Cabe resaltar que, para llevar a cabo el diseño y el modelamiento del rotor a escala con la teoría de modelos, es indispensable tener información de las características geométricas de un prototipo de rotor ―en este estudio, específicamente, un rotor Darrieus en H―. Las características del flujo ―como la velocidad― dependerán de la zona en la que se quiera hacer uso de dicho prototipo. De esta manera, se intuye que debemos garantizar la semejanza de flujo para el modelo de laboratorio si se desea saber qué está sucediendo con el prototipo en campo. La metodología fue la siguiente.
Consulta de rotores de eje vertical Darrieus H
Para la investigación, fue de vital importancia consultar diferentes tipos de rotor de eje vertical, con énfasis en rotores Darrieus H, debido al criterio del diseñador. Luego de consultar, se evidenció que no es extendido y que no existe mucha documentación sobre el uso de este tipo de rotores en el desarrollo de bancos para laboratorio, por lo cual, en un gran aspecto, se está innovando.
De diferentes tipos de estudios, se puede resaltar el de Geovo y González (2015), en el departamento de Córdoba, Colombia, quienes nos muestran que a través del modelado analítico DMST ―double multiple stream tube―,
se logró optimizar el alabe con el perfil NACA 0025 del aerogenerador VAWT, dejando como resultado una dimensión del alabe con una longitud de 2 m de altura, una longitud de cuerda del perfil de 0,55 m y un diámetro del rotor de 2.6 m, obteniendo con esto un incremento de la potencia captada nominal de 17.19 W hasta 45.57 W y una potencia máxima aproximada de 400 W y un torque máximo de 43 n. m. Se logra, adicionalmente, la condición de autoarranque para un viento mínimo de 2.5 m/s. (p. 47)
En ese trabajo, se diseñó y se modeló la geometría de un prototipo de turbina Darrieus, a la cual se aplicó el proceso matemático para realizar su reducción.
Teorema de Π de Buckingham
El teorema de Π de Buckingham permite obtener expresiones matemáticas a partir del análisis dimensional con las cantidades físicas implicadas en el problema a resolver.
Para que los resultados obtenidos en un modelo físico sean extrapolables al prototipo real, se deben satisfacer dos criterios:
Primero: el modelo y el prototipo deben ser geométricamente similares. La similitud geométrica puede establecerse mediante una escala de longitudes como la razón entre el prototipo y el modelo.
Segundo: el modelo y el prototipo deben ser dinámicamente similares. La similitud dinámica establece que los dos sistemas con fronteras geométricamente iguales tengan patrones de flujo geométricamente similares, en instantes de tiempo correspondientes. Esto requiere que todas las fuerzas individuales que actúan sobre elementos correspondientes de fluido tengan las mismas razones (proporciones) en los dos sistemas. (Domingo, 2003, p. 6)
Con esta herramienta teórico-matemática, se determinaron variables de flujo y variables geométricas para obtener las igualdades que gobernarían el desarrollo de dicho rotor de eje vertical. Como resultado se obtuvieron dos expresiones: el número de Reynolds y una simple escala geométrica que relaciona la altura y diámetro del prototipo, o bien la altura de cada alabe con la cuerda del mismo. Esta relación se conoce como relación de aspecto y entabla un cociente entre las magnitudes mencionadas.
Una vez recopilados los datos de entrada, se obtuvieron las variables de salida. Luego, se procedió con el análisis dimensional teorema Π de Buckingham y se desarrolló el flujograma que se muestra en la figura 1.
Figura 1
Flujograma de la metodología para aplicar el teorema
A partir de la metodología planteada para esta sección y luego de hacer los cálculos necesarios, se obtuvieron las siguientes ecuaciones.
En primera instancia, se han de mencionar las características que definen el problema, como se enlista en seguida:
- Características geométricas: longitud (L)
- Características dinámicas: velocidad (V)
- Características del fluido: viscosidad (v)
Cada característica posee dentro de sí una variable que se define como magnitud física, que a su vez representará un parámetro n dentro del desarrollo del problema. Entonces, se realiza una revisión a cada una de las características para obtener los parámetros n. Ordenamos los parámetros n que solicita el teorema de la siguiente manera:
- Características geométricas: diámetro (D), altura (A); en metros (m).
- Características dinámicas: velocidad de viento (V); en metro sobre segundo (m/s).
- Características del fluido: viscosidad cinemática(v); en metro cuadrado sobre segundo (m2/s).
Obsérvese que n=4.
Ahora, cada parámetro n se deja indicado en sus dimensiones primarias, como se muestra en la ecuación 1.
D[m1];A[m1]; V[m * s–1]; v[m2 * s–1] (1)
Al establecer una reducción de parámetros repetitivos j como el número de dimensiones primarias presentes en el problema, obtenemos la ecuación 2.
j=2 (2)
Como se observa en la ecuación 1, solo existen como unidades básicas el metro y el segundo. Una vez establecidas las cantidades de j y n, se determina k, como se muestra en la ecuación 3.
k=n – j
k=4 – 2 = 2 (3)
Entonces se determina que k = 2. Los grupos adimensionales π son formados al usar k y combinar los parámetros repetitivos j, que por lo general son los que poseen las magnitudes físicas más simples presentes en el problema. Para este caso, se establece que una altura tiene la magnitud física de la longitud y la velocidad posee la magnitud física de la longitud y el tiempo. Así, al combinar los parámetros restantes ―viscosidad cinemática y diámetro― con los j, se adicionan arbitrariamente exponentes a los parámetros j con las letras a1, b1, para el grupo adimensional 1; y exponentes con letras a2, b2, para el grupo adimensional 2, como se muestra en las ecuaciones 4 y 5.
π1= D * Aa1 * Vb1 (4)
π2= v * Aa2 * Vb2 (5)
Escribimos los parámetros en unidades básicas e igualamos los grupos adimensionales con las dimensiones primarias con exponente igual a cero para forzar a π a ser adimensional (ecuación 6).
[L0T0]=[L1 * La1*(L1 * T –1)b1] (6)
La ecuación para unidades de longitud y de tiempo es segregada (ecuación 7).
[L0]=[L1 * La1* Lb1] (7)
Los exponentes son expresados de la siguiente manera en una igualdad (ecuación 8).
[0]=[1 + a1+ b1] (8)
La ecuación 8 es solucionada y se obtiene:
[–1]=[a1+ b1] (9)
El mismo procedimiento es realizado para la magnitud de tiempo (ecuación 10).
[T0]=[T – b1]
[0]=[– b1]
b1 = 0 (10)
Por lo tanto, se tiene que el exponente b1 será igual a cero, entonces a1 tendrá un valor de -1.
Al remplazar exponentes en la ecuación 4, resulta:
π1= D * Aa1 * V0 (11)
Luego de realizar operaciones y acomodar la ecuación 11, se observa que la expresión denota una relación de longitudes, lo que se deduce como una relación geométrica de escala (ecuación 12).
π1= D/A (12)
Después se procede a realizar la misma operación para el grupo adimensional 2, y se obtiene de la ecuación 13 a la ecuación 20.
Se organiza todo de manera que se expresen las magnitudes como letras, unidades de tiempo y longitud para este caso.
[L0T0]=[L2 * T –1* La2*(L1 * T –1)b2] (13)
Dos ecuaciones son generadas a partir de la ecuación 13: una para unidades de longitud (L) y otra para unidades de tiempo (T).
[L0]=[L2 * La2* Lb2] (14)
Realizamos operaciones con exponentes y obtenemos la ecuación 15.
[0]=[2 + a2+ b2] (15)
[–2]=[ a2+ b2] (16)
El mismo procedimiento es realizado con la variable tiempo (T) (ecuación 17).
[T0]=[T – 1 * T – b2 ]
[0]=[–1 – b2]
[b2]=[–1]
[a2]=[–1] (17)
Al obtener los exponentes con subíndice 2, se reemplazan en la ecuación 5 y resulta la ecuación 18.
π2= v1 * A–1 * V – 1 (18)
Luego de reescribir la ecuación 18, se obtiene:
π2= v/A*V (19)
Se puede observar que la ecuación relaciona fuerzas viscosas con fuerzas inerciales. El teorema nos indica que es el número de Reynolds. Se reescribe la ecuación 19 para obtener la ecuación 20.
π2= A*V/ v (20)
Recuérdese que, para cada uno, modelo (m) y prototipo (p), existirán dos grupos adimensionales. Es decir, si se organizan las expresiones obtenidas mediante el teorema de Π de Buckingham, son 4 igualdades en total.
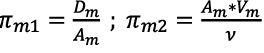 (21)
(21)
+
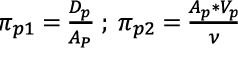 (22)
(22)
El grupo adimensional 1 del modelo se iguala con el grupo adimensional 1 del prototipo, así como con el grupo adimensional 2, con lo que se termina el proceso matemático para determinar las ecuaciones que gobiernan el diseño del modelo.
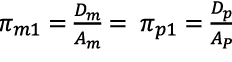 (23)
(23)
 (24)
(24)
Aplicación del teorema de Π de Buckingham
Para obtener las dimensiones del modelo de rotor Darrieus H, se usan las ecuaciones 21 y 22. Las características geométricas del prototipo de rotor Darrieus en H mostradas en la figura 1 son listadas a continuación:
- altura del prototipo: 2 m (AP)
- diámetro del prototipo: 2.6 m (Dp)
- perfil aerodinámico del prototipo: NACA 0025
- cuerda del perfil del prototipo: 0.55 m (Cp)
- número de aspas ―perfiles―: 3
En este punto, se resalta que, para la realización del modelo de laboratorio de rotor Darrieus H, se consideró una altura máxima de modelo de 38 cm, puesto que las maquinas-herramientas disponibles para realizar dicho rotor disponen de una longitud de mecanizado y de impresión máxima de 19 cm * 19 cm. Por lo tanto, se intuye que la pieza realizada será elaborada en dos secciones. Dicha altura también tiene una estrecha relación con la velocidad de viento requerida, lo que se explicará en esta sección.
Al remplazar valores en la ecuación 23, se obtiene el diámetro del modelo (Dm)
.
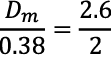
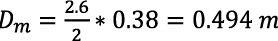 (25)
(25)
Una vez calculado el valor del diámetro del modelo (Dm,) el factor de escala es determinado como se muestra en la ecuación 26.
 (26)
(26)
Entonces, al conocer el factor de escalas, la cuerda del modelo de laboratorio es determinada (ecuación 27).
Cm = 0.55m * 0.19
Cm= 0.1045 m (27)
Se definen las características geométricas de nuestro modelo de rotor Darraieus H de la siguiente manera.
- altura del modelo: 0.38 m (Am)
- diámetro del modelo: 0.494 m (Dm)
- perfil aerodinámico del modelo: NACA 0025
- cuerda del perfil del modelo: 0.1045 m (Cm)
- número de aspas ―perfiles―: 3
Ahora se definen los parámetros con el segundo grupo adimensional, que hace referencia al número de Reynolds. Como se mencionaba antes, para que exista una relación entre prototipo y modelo, los números de Reynolds tanto para el prototipo Rep como para el modelo Rem, deben ser iguales. Por lo tanto:
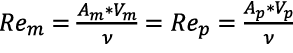 (28)
(28)
Por ahora, no es de interés saber en qué régimen de flujo se encuentra el fluido. Se asume que los números de Reynolds son iguales, modelo y prototipo. La viscosidad cinemática se cancela (ecuación 29).
Am * Vm = Ap * Vp (29)
De la ecuación 29 se despeja la velocidad del modelo Vm que se requiere en laboratorio para cumplir con la semejanza dinámica establecida por el número de Reynolds. Para este caso se usó una velocidad de viento en una zona donde equivale a 3 m/s.
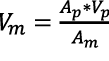
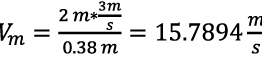 (30)
(30)
Como se aprecia en la ecuación 30, la altura del modelo se relaciona estrechamente con la velocidad requerida por él. Son inversamente proporcionales. Al reducir la altura a la longitud máxima de trabajo de las máquinas-herramientas, la velocidad toma un valor considerablemente alto. Esto hace más difícil la obtención de dicha velocidad en laboratorio. Hasta este punto se finaliza el proceso matemático del diseño. Ahora las siguientes secciones hacen referencia al cálculo de otros equipos y del diseño mecánico del banco.
Selección del equipo de generación de corriente de viento (ventilador-extractor)
Establecida la velocidad de viento requerida para el modelo, se calcula el régimen en el que se encontrará el fluido, tanto para el prototipo como para el modelo (ecuaciones 31 y 32).
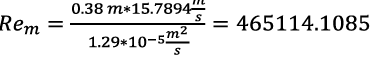 (31)
(31)
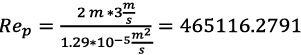 (32)
(32)
Esencialmente, el número de Reynolds del prototipo y del modelo son el mismo. Se establece que el régimen para ambos es un régimen de turbulencia totalmente desarrollada, puesto que el régimen de turbulencia empieza a apreciarse a partir de un número de Reynolds de 4000 en adelante. En este caso, se tiene un Re de 465000.
Se hizo una búsqueda de diferentes tipos de ventiladores y extractores para saber cuál de ellos sería el idóneo. Para esta aplicación se tuvieron en cuenta variables como el diámetro y el caudal para realizar el cálculo de la velocidad máxima ofrecida por el ventilador-extractor. La información se organizó en una tabla y finalmente se seleccionó un ventilador-extractor axial idóneo, cuyas características se muestran en la tabla 1.
Tabla 1
Características del ventilador-extractor seleccionado
|
Motor / especificación
|
Diámetro del rotor (m)
|
Área de ventilación (m2)
|
Caudal (m3/h)
|
Velocidad máx. de trabajo (m/s)
|
|
TRIFÁSICO 2HP (1700 RPM)
|
0,635
|
0,316692174
|
21060
|
18,47219626
|
La velocidad requerida por el modelo es de 15.7 m/s. La velocidad que ofrece el equipo seleccionado es de 18.4 m/s, por lo que se tiene un margen para evitar usar el equipo a su capacidad máxima. Así mismo, para no hacer uso del equipo al 100 %, se seleccionó un equipo variador de frecuencia para regular la velocidad de salida generada por el ventilador.
Tabla 2
Características del variador de frecuencia para ventilador-extractor
|
Marca
|
Características
|
|
Electromecánica & Automatización Ind.
|
2hp - 220 vac trifásico 600hz
|
Diseño mecánico del banco eólico de eje vertical
Este diseño se subdividió en dos partes. Por un lado, el soporte y los componentes del rotor de eje vertical Darrieus H (figuras 2 y 2a); y, por otra parte, un túnel de viento y la estructura que soporta el ventilador y el túnel de viento (figuras 3, 4 y 5).
Diseño mecánico del rotor de eje vertical. Una vez establecidas las medidas ―cuerda, altura, diámetro― y características como el perfil aerodinámico y el número de aspas, se planteó un diseño del modelo que incluyó un sistema que permitiera desacoplar el rotor de la base para la instalación y uso de diferentes rotores. De igual manera, la estructura soporte de las aspas permitirá el cambio del ángulo de ataque de estas.
Sistema de acople a la base del banco-varilla roscada. Para facilitar el ensamble del rotor a la base, se seleccionó una varilla roscada que permitiera sujetar al rotor de manera firme. Para asegurar que, durante su funcionamiento, no se desajustara, se seleccionaron dos tuercas a manera de contratuerca en cada uno de los extremos para asegurarlo. Esto facilita el proceso de instalación y de desinstalación. También es una manera efectiva y sencilla para lograr el uso de diferentes rotores sin mayor inconveniente, como se puede apreciar en las figuras 2 y 2a.
Figura 2
Vista lateral eje de acople

Figura 2a
Detalle. Tuercas de aseguramiento.

Modificación del ángulo de ataque. Perfil aerodinámico. Para facilitar el cambio del ángulo de ataque del perfil aerodinámico, se realizaron perforaciones en su centro y en los extremos en la parte superior (figura 3). Así, existen dos agujeros de 10 mm ubicados en el centro en cada uno de los extremos y dos agujeros de 5 mm en la cara superior para facilitar la sujeción a diferentes ángulos de ataque, comprendidos entre 0° y 30°.
Figura 3
Agujeros de sujeción y modificación de ángulo de ataque

Láminas sujetadoras. Seis láminas de aluminio permiten asegurar el perfil NACA a su posición de trabajo (figura 4). De esta manera, se diseñaron y se construyeron tres láminas que tienen unos pequeños radios en uno de sus extremos, lo que permite un recorrido semicircular que barre ángulos comprendidos entre 0° y 30°; y tres láminas más que poseen agujeros sencillos en sus extremos.
Figura 4
Láminas sujetadoras

Discos de sujeción. Para sujetar con facilidad las láminas y asegurar el eje roscado en su correspondiente posición, se diseñaron y se construyeron dos discos de acero, cuyo CAD se aprecia en la figura 5. Tienen un agujero central que permite el paso de la varilla roscada y agujeros dispuestos a 120° de distancia entre sí, de 8 mm de diámetro, que coinciden con las seis láminas, que de la misma manera tienen agujeros de 8 mm de diámetro en uno de sus extremos, lo que permite que se atornille entre discos y láminas.
Figura 5
Disco de sujeción

Figura 6
Modelo CAD del rotor de eje vertical Darrieus

Diseño mecánico del túnel de viento y estructura
Túnel de viento. Consta de una lámina rolada que forma un cilindro hueco de 1.5 mm de espesor, cuyo diámetro interior es de 70 cm y posee una longitud de 1.80 m, que se puede observar en la figura 7. En su interior se dispuso una malla que cumple el propósito de enderezar el flujo de aire a través del túnel. La distancia del túnel se calculó según la longitud de desarrollo de flujo turbulento. El diámetro se calculó especialmente para que las paredes del túnel no interfirieran con el desplazamiento del rotor.
Modelo CAD del túnel de viento del banco eólico de eje vertical

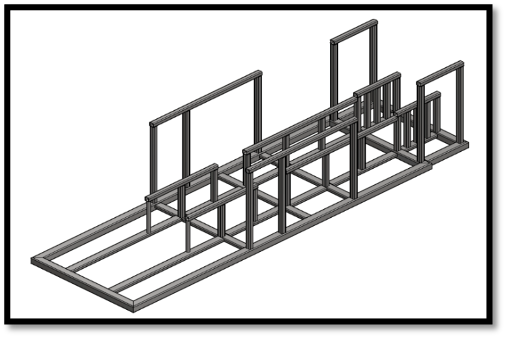
Estructura metálica o esqueleto del banco. Las medidas seleccionadas para la estructura se hicieron según la longitud y diámetro del túnel y del ventilador seleccionado. Consta de perfilería metálica cuadrada y soporta aproximadamente 70 kg de peso del túnel de viento y del ventilador. La figura 8 muestra el diseño CAD de la estructura.
Figura 8
Modelo CAD de la estructura, soporte del banco eólico de eje vertical
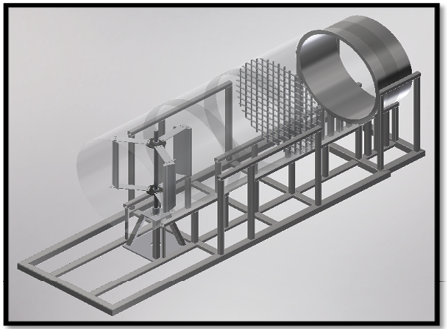
Modelo CAD del banco eólico de eje vertical. Finalmente se obtuvo el modelo CAD que se puede apreciar en la figura 9, en donde se ve el conjunto de los elementos ensamblados y, en su interior, el modelo de turbina eólica de eje vertical. En la figura no se ven las aspas del ventilador que está dispuesto al final de la estructura, puesto que para el montaje solo es necesario conocer las dimensiones de la carcasa.
Figura 9
Modelo CAD del banco eólico de eje vertical
Resultados
Se logró obtener el diseño en computadora ―CAD― con los parámetros geométricos y de flujo para cumplir con las relaciones de semejanza establecidas. Así mismo se levantaron planos de las piezas que hacen parte del banco eólico de eje vertical, planos que se usarán luego para construir lo desarrollado en este estudio. Después se verá reflejado el componente práctico con base en el componente teórico.
Las expresiones obtenidas a través del desarrollo matemático muestran la dominancia de diferentes números adimensionales en el desarrollo del diseño presentado. Sin embargo, existe uno que predominará frente a los otros resultados, en este caso. Como ampliamente se usa en mecánica de fluidos, el número de Reynolds fue clave para sustentar el componente teórico y obtener así las características del flujo y los parámetros obligatorios para corroborar resultados de campo en el laboratorio.
El diseño mecánico obtenido estuvo parametrizado por diferentes elementos, que se pueden clasificar de la siguiente manera:
- elementos de construcción ―según la capacidad de los equipos para realizar dichos componentes―.
- elementos de medición ―los dispositivos disponibles en laboratorio para realizar prácticas―.
- elementos de prueba ―en este caso, el equipo generador de corriente de viento―.
Conclusiones
El uso de las herramientas matemáticas facilita el estudio de diferentes fenómenos físicos presentes en la vida cotidiana y también en problemas de alta ingeniería. Esto representa un gran ahorro de recursos a la hora de realizar mediciones y pruebas con modelos de equipos máquinas ya existentes o ―en un caso más avanzado― en el desarrollo de nuevas tecnologías y máquinas sin tener que construir grandes y dispendiosos prototipos que tendrán un solo uso.
En el desarrollo de un equipo se involucran diferentes variables. A pesar de mostrarse independientes una de la otra, existe una conexión entre todas ellas. Es decir, no se puede construir un túnel de viento sin saber las medidas del modelo que habitará dentro de él. Así mismo, no se podrá construir un esqueleto sin saber las medidas y los espacios requeridos. En teoría de modelos se observa que dos variables ―como lo son la velocidad y la longitud― se relacionan entre sí. A medida que disminuye una de ellas y se acomoda a la disponibilidad de equipos ―en este caso, velocidad de viento―, automáticamente la segunda subirá de valor. Esto obliga a encontrar el punto intermedio para llevar la idea teórica a la práctica más ajustada a la capacidad de producción, a la matemática planteada y al factor monetario.
De esta manera, al desarrollar e innovar con teorías y materiales poco frecuentes en esta rama de la ingeniería, el impacto social y educativo tiene más valor, puesto que se hacen más visibles ciertas definiciones y formas de resolver problemas de la vida cotidiana.
Con las diferentes herramientas teórico-matemáticas de la ingeniería, se facilita el diseño y la construcción de nuevos dispositivos que pueden abrir la puerta al desarrollo de una comunidad o bien aportar a la bibliografía. Al crear experimentos caseros que permiten reforzar conocimiento básico en mecánica de fluidos y diseño mecánico, el estudiante de ingeniería podrá tener contacto directo con máquinas semejantes a un módulo industrial, lo cual facilita las prácticas y aumenta la creatividad en el momento de plantear soluciones a problemas de ingeniería.
Este documento abre un sinfín de ventanas al mundo del diseño y del estudio en mecánica de fluidos. El uso del banco eólico de eje vertical permitirá el reconocimiento de diferentes tipos de rotores de eje vertical en H, al variar el espesor, el alto y la cuerda del tipo de perfil usado ―NACA, etc.—. La motivación de esto es profundizar en el estudio de las energías renovables, puesto que, indirectamente, durante todo el diseño de este producto, se tuvo en mente el propósito de usar energías alternativas a las fósiles.
Referencias
Busquets, D. (2011). Diseño y fabricación de los alabes de un micro-aerogenerador de baja potencia. Tesis de grado, Universitat Politècnica de Catalunya]. UPCommons. http://hdl.handle.net/2099.1/17771
Domingo, R. (2003). Estudio teórico-experimental de un sistema de disipación de energía poco habitual al pie de una caída de agua [Tesis de grado, Universitat Politècnica de Catalunya.], base de datos, http://hdl.handle.net/2099.1/6002
Escuela Politécnica Superior de Ingeniería de Gijón Ingenieros Industriales. (s. f.). Curso 2004-2005.
Geovo, L., & González, A. (2015). Diseño y modelamiento de la geometría del perfil alar de un aerogenerador, basado en las condiciones de viento presente en el departamento de Córdoba para la generación de potencia [Trabajo de grado, Universidad de Córdoba]. Repositorio Universidad de Córdoba. https://repositorio.unicordoba.edu.co/handle/ucordoba/702
Sánchez, J. (2017). Diseño de una balanza para túnel de viento subsónico [Disertación doctoral no publicada]. Universitat Politècnica de València.

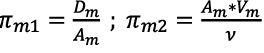 (21)
(21)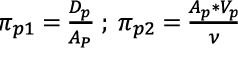 (22)
(22)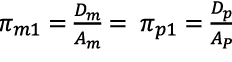 (23)
(23)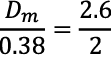
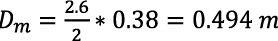 (25)
(25)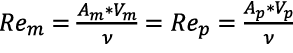 (28)
(28)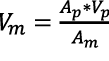
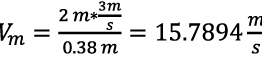 (30)
(30)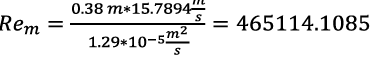 (31)
(31)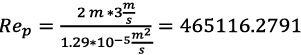 (32)
(32)




