Manuel Suárez Martínez ―1941-2020―, profesor emérito e investigador de la Escuela de Matemáticas y Estadística de la Universidad Pedagógica y Tecnológica de Colombia [UPTC], fue miembro del grupo de investigación Vialtopo, mediante el cual fomentó el estudio de la topología conjuntista de la mano de reconocidos profesores de la Universidad Nacional de Colombia [UNAL] y de la Universidad del Valle [Univalle]. Entre sus trabajos investigativos de mayor reconocimiento están: Criterios de convergencia secuencial (Suárez & Torres, 1982), La función topológica Hunza (Suárez, 1988), Funciones de núcleo o topologías (Suárez & Torres, 1990), Un ejemplo de álgebra booleana (Suárez, 1992b), El grupo de Klein y la teoría de la adjunción en la topología conjuntista (Suárez, 1994), Hacia una revisión de la topología conjuntista: utilizando como referentes a O. Ore, G. Boole, F. Klein, K. Kuratowski y J. Adamek (Ruiz & Suárez,1995), entre otros, los cuales configuran la base de su libro Topología general. IV parte (1995), que puede considerarse como el compendio de su vida investigativa en topología conjuntista.
Por otra parte, el profesor Suárez se preocupó por exponer de una forma clara, estructurada y accesible todo su conocimiento. Desarrolló cursos de topología que le permitieron ser admirado e incluso reconocido como un modelo a seguir por parte de sus estudiantes, en virtud de su disciplina de estudio y sus estrategias didácticas. En efecto, el libro Elementos de topología, que realizó junto a Carlos Ruiz Salguero en dos ediciones (1975, 1976), es la evidencia de su compromiso con el establecimiento de elementos didácticos diferentes y eficaces para la enseñanza y aprendizaje de la topología. En él se encuentra una guía a partir de la cual estudiantes y profesores pueden desarrollar un curso de topología general de una forma constructiva.
En este artículo se describe la acción didáctica e investigativa de Manuel Suárez, su alcance y su legado en la formación de profesores de matemáticas en la UPTC. Para tal efecto, iniciamos con algunos datos biográficos, sus pasiones y motivaciones, que siempre estuvieron ligadas al desarrollo de su formación académica y de su vida laboral. Así, detallamos sus principales reconocimientos y logros. En la segunda parte se tratan aspectos relacionados con su actividad como investigador. Precisamos los temas trabajados, grupos de investigación, publicaciones y eventos que dirigió y en los que participó. La tercera parte describe su labor docente, tema en el cual se revelan sus estrategias didácticas a partir de entrevistas de quienes fueron sus estudiantes y de sus publicaciones. Finalmente, se discute el alcance de su obra en la formación de una nueva generación de docentes de la UPTC, el fomento y la formalización de la investigación en matemáticas de dicha universidad, así como la incorporación de nuevos enfoques pedagógicos en las clases de topología.
Manuel Suárez, de matemáticas
Manuel Suárez Martínez nació en 1941 en San Gil ―Santander― e inició sus estudios en el Colegio Nacional San José de Guanentá de ese municipio. Desde sus primeros años de estudio ya conocía del caballete, la gramática y los grandes maestros de la pintura, arte que le abrió puertas hacia otros espacios y otras dimensiones del espíritu y del conocimiento:
Cuando apenas era un niño, realizando una tarea de ciencias naturales, al sembrar una semilla de maíz y ver cómo se desarrollaba la planta, me asombré con agrado de las maravillas de la naturaleza. Desde entonces inició mi interés y pasión por la ciencia. (M. Suárez, entrevista personal, 23 de septiembre, 2014)
Estudió durante tres años en la Facultad de Ingeniería de la Universidad Industrial de Santander [UIS], la cual abandonó después de un enfrentamiento entre el Ejército Nacional y los estudiantes, donde involuntariamente se encontraba en medio del disturbio y fue retenido por algunas horas. En 1967 se trasladó a la UPTC ―Tunja― (Imagen 1), en donde se graduó de la Licenciatura en Matemáticas y de la Licenciatura en Física en 1971, al obtener grado de honor por su desempeño académico.
Poco después de su titulación, fue designado como profesor en la UPTC, donde fue profesor titular. Dirigió también algunas cátedras en la UNAL y en la UIS. En su búsqueda por conocer la forma de crear matemáticas, terminó inmerso en el mundo de la topología y conoció al profesor Carlos Ruiz Salguero, quien se convirtió en su asesor, compañero de investigación y gran amigo. En 1971, el profesor Suárez inició sus estudios en el programa de Especialización en Matemática Avanzada de la UNAL. Allí se graduó con honores gracias a su trabajo La Función Topológica Hunza (1988), trabajo que fue expuesto en The Northeast conference on general topology and its applications (1989) de Nueva York. Su profundo aprecio y agradecimiento con la ciudad de Tunja ―Hunza― quedó inmortalizado en este trabajo, que fue entregado en ceremonia de honor al Concejo Local, el cual le retribuyó otorgándole las llaves de la ciudad.
El camino que siguió el maestro Suárez para posicionarse como investigador no fue sencillo, puesto que su innovadora función Hunza fue su primera publicación reconocida por la comunidad científica internacional, luego de muchos rechazos:
Cuando empecé mi producción de artículos, encontré muchos obstáculos. El principal era la falta de bibliografía actualizada de topología en el país. Yo establecía diferentes resultados que ya habían sido publicados por alguien más en el mundo y solo me enteraba cuando rechazaban mis trabajos en revistas y congresos. (M. Suárez, entrevista personal, 23 de septiembre, 2014).
De esta manera inició su producción matemática y contrajo, como él lo decía, matrimonio con las matemáticas, por lo que se presentaba jocosamente como “Manuel Suárez, de matemáticas”. En medio de ese amor, decidió continuar su formación académica y cursó la Maestría en Ciencias Básicas con énfasis en Matemáticas ofrecida por la UNAL. Finalizó este programa en 1994 con el trabajo de grado laureado El grupo de Klein y la teoría de la adjunción en la topología conjuntista.
Imagen 1
Manuel Suárez Martínez

Nota. Fotografía presentada como requisito de ingreso a la UPTC (1967).
Alcances de su investigación en topología conjuntista
Manuel Suárez fue partícipe de varios proyectos de investigación desarrollados entre la UPTC y la UNAL, la mayoría de ellos dentro del grupo de investigación Vialtopo, que era dirigido por Carlos Ruiz Salguero. En este grupo estaban vinculados inicialmente los grupos de trabajo en topología de la UNAL, Sede Bogotá ―coordinado por el profesor Carlos Ruiz Salguero―, de la Univalle, Cali ―orientados por el profesor Roberto Ruiz―, y de la UPTC, donde el profesor Manuel Suárez Martínez fungía de líder. El trabajo en este grupo era desarrollado a partir de una visión algebraica de la topología y se utilizaban enfoques: filtrado ―en Bogotá―, booleano ―en Bogotá y Tunja―, adjunto ―en Bogotá y Tunja― y homotópico ―en Bogotá y Cali―. En todos los casos tuvo como sustento común el enfoque categórico. Se desarrollaban dos actividades en el grupo, El Encuentro de Topología ―semanal― y El Encuentro de Topología ―semestral―.
En su primer proyecto de investigación, denominado Enseñanza de la Topología (1974-1976), se obtuvieron diferentes trabajos. El más notorio de ellos Elementos de topología ―cuadernos 1 y 2― (1975, 1976), trabajos realizados con Carlos Ruiz Salguero, con el auspicio de Colciencias, en el marco del V Coloquio de Matemáticas (Medellín, 1976) y como publicación de Colciencias en el VI Coloquio de Matemáticas (Bogotá), respectivamente.
Durante cinco años ―1976-1981―, el profesor Suárez fue designado como coordinador de la Especialización en Matemática Avanzada, que se realizaba en convenio entre la UPTC y la UNAL, años durante los cuales inició su participación en la Sociedad Boyacense de Matemáticas y Física ―1979― como organizador y ponente. “Era un increíble expositor, que tomaba un auditorio con medianos conocimientos en topología y durante la ponencia lo llevaba en un proceso de reconstrucción, elevando el nivel hasta llegar con todos los presentes al resultado que él había encontrado” (M. Álvarez, entrevista personal, 29 de noviembre, 2014).
Ya en 1982, inició su segundo proyecto de investigación denominado Convergencia Secuencial, proyecto que desarrollado durante cuatro años consecutivos, en el cual profundizó en los temas expuestos en su publicación Topología o convergencia (Ruiz & Suárez, 1980).
Su tercer proyecto, titulado Topología general, se desarrolló en cinco partes, desde 1984 hasta 2002 ―18 años―. Trabajó con las nociones booleanas, en la búsqueda de nuevas clases de espacios topológicos. Las nociones de la adjunción de funciones le permitieron fundamentar propiedades topológicas y explicar los isomorfismos existentes. Entre los resultados de este proyecto sobresalen los 15 trabajos de grado que dirigió en la Especialización en Matemática Avanzada de la UNAL, el artículo Funciones de fundamental o topologías booleanas desarrollado con Germán Torres Roa (1992), y también trabajos como Un ejemplo de álgebra booleana (1992b), Topologías asociadas con el álgebra de Boole PX (1991) y Estructuras sintopógenas y topologías (Lineros & Suárez, 1999).
Asimismo, el profesor Suárez fue fiscal de La Sociedad Colombiana de Matemáticas ―1987-1989― y secretario de 19 Encuentros de Topología, que se desarrollaron entre 1987 y 1997. En los años siguientes ―1991-1993―, fue director de las cinco primeras Jornadas de Matemáticas de la UPTC y miembro del comité organizador de las siguientes nueve ediciones hasta 1997. Enfocó su atención en las actividades de su proyecto de investigación alterno Matemática Educativa, que inició en 1993.
Por otra parte, entre los trabajos del profesor que aún no se han mencionado están: sus libros Topología conjuntista: una presentación booleana adjunta (Suárez, 1992a) y su continuación (Suárez, 1993b); su trabajo docente La función topológica de exterior (Camacho & Suárez, 1987); y sus artículos Conjuntos fronterizos (Gómez & Suárez, 1992) y Álgebras booleanas de cuantificadores (Suárez, 1993a).
Entre sus participaciones como ponente se destacan: el I Coloquio Bolivariano de Matemáticas en Quito ―Ecuador― el año 1990 con su conferencia: Funciones adjuntas en topología general; el I Congreso Iberoamericano de Topología realizado en Valencia ―España― en enero de 1995, con su trabajo: Hacia una revisión de la topología conjuntista: utilizando como referentes a O. Ore, G. Boole, F. Klein, K. Kuratowski y J. Adamek; el II Congreso Iberoamericano de Topología que se realizó en Morelia ―México― con la ponencia intitulada Conjuntos trivialmente compactos (Suárez & Suárez, 1997); el III Congreso Iberoamericano de Topología realizado en Gandía ―España― con la ponencia titulada Estructuras sintopógenas y topologías (Lineros & Suárez, 1999); el IV Congreso Iberoamericano de Topología realizado en abril de 2001 en Coímbra ―Portugal―, con la conferencia La noción topológica de m-filtro; y finalmente la investigación titulada Spring Topology and Dynamical Systems (2003), socializada en Texas ―Estados Unidos―, en el encuentro Joint Maps and Supratopologies.
Su legado en la formación de docentes y en la didáctica de la topología
El profesor Suárez tenía una idea clara: “La matemática no es difícil, solo hay personas egoístas que no saben cómo enseñarla” (M. Suárez, entrevista personal, 23 de septiembre, 2014), forma de pensar que lo acompañó durante toda su vida, como lo resaltó el periódico El Tiempo:
Su principal tarea como educador, investigador y científico ha sido promover la humanización de la enseñanza de las matemáticas. Para él lo importante no es la capacidad de resolver operaciones, sino la manera de construir nuevos pensamientos, y que el hombre tenga una nueva concepción de la vida desde esta perspectiva. (Redacción El Tiempo, 2000)
Su legado en la didáctica de la topología conjuntista es considerado a partir de sus prácticas, descritas como resultado de entrevistas a profesores de la UPTC que fueron sus estudiantes, cometido para el cual se construyó una red de análisis de la información. En la figura 1 se presentan las categorías principales que se obtienen de la implementación de la teoría fundamentada (Corbin & Strauss, 2002), cuya interpretación se presenta a continuación.
Figura 1
Red de categorías principales de análisis
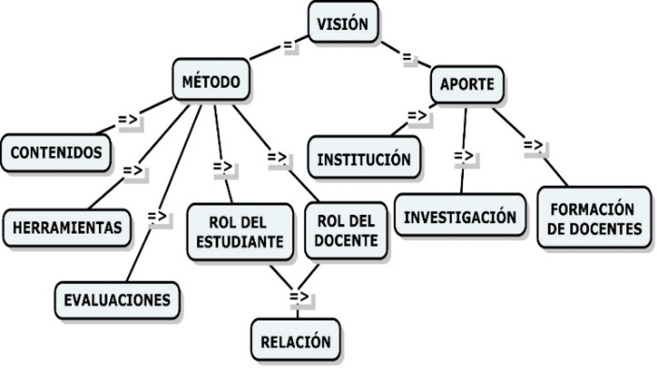
Nota. Realizado mediante ATLAS.ti 6.
Modelo pedagógico
El desarrollo de la enseñanza de la topología por parte del profesor Manuel Suárez se puede catalogar como constructivista, ya que en sus clases lo importante era que cada estudiante descubriera su propia forma de aprender, objetivo para el cual proponía actividades:
Absolutamente todo el tiempo mantenía al estudiante pensando: él iniciaba una clase haciendo un repaso y avanzaba en el tema gradualmente, siempre trabajando con base en diagramas que se elaboraban a partir de las ideas de los estudiantes y de preguntas del profesor para enlazar todo. Los avances no seguían un texto en especial, sino que se iban generando las propiedades. (F. Leguizamón, entrevista personal, 31 de julio, 2014)
Cada clase era iniciada con algún comentario de una situación cotidiana que invitaba a los estudiantes a un debate, a partir del cual se retomaba lo visto anteriormente, y luego se encauzaba la discusión hacia el tema previsto para la sesión.
Él intentaba que nosotros [estudiantes], que no es fácil por supuesto, visualizáramos los conceptos topológicos en situaciones concretas y hacía algunas comparaciones. Por ejemplo, en el caso de la métrica empezaba con algún comentario sobre el tráfico o alguna vía en mal estado y proponía una conversación en donde se comparaba la distribución de las calles y manzanas de algunos pueblos de Santander y Boyacá con la forma en que se determinaban distancias. (H. Manrique, entrevista personal, 12 de marzo, 2014).
Los anteriores elementos permiten relacionar la metodología del profesor Suárez con lo que Coll (1990) denomina las tres ideas fundamentales de la concepción constructivista: el estudiante es el responsable de su propio proceso de aprendizaje; la actividad mental constructiva del alumno se aplica a contenidos que poseen ya un grado considerable de elaboración; y la función del docente es enlazar los procesos de construcción del estudiante con el saber colectivo culturalmente originado. Como valor agregado se tiene la productividad de sus clases, que imponen altos niveles de exigencia mientras contextualizan el conocimiento y apuntan a la interdisciplinariedad, al apoyarse en el trabajo continuo, el desarrollo de actividades grupales y el buen uso del tiempo.
Rol del profesor
El profesor Suárez siempre trabajaba con la mejor energía, dispuesto a aprovechar cada instante en el aula y fuera de ella. Se preocupaba por que cada estudiante se mantuviera activo en la clase, es decir, que estuviera atento a todo lo que se hacía o se construía, lo que garantizaba su participación y su aprendizaje. Todo lo anterior es recordado por Miguel Arcángel Díaz con las siguientes palabras:
Lo que más recuerdo de las clases de él, el dinamismo con el cual abordaba las temáticas, la energía que irradiaba frente al grupo, el ambiente que creaba con su aspecto bastante imponente, pero a la vez muy accesible. Manejaba el espacio del salón de clase de una manera dinámica. Él se la pasaba recorriendo el salón y permanentemente estaba indagando al estudiante para poder ir llenando lo que él estaba construyendo en el tablero, mediante diagramas muy bien pensados que conducían al logro de las demostraciones, manejando un tono de voz que era bastante impactante en el sentido de irradiar energía. Las clases de él eran bastante activas y muy amenas. (M. Díaz, entrevista personal, 17 de junio, 2014)
Ahora bien, para reforzar el logro de una actitud activa del estudiante, el profesor se convertía en la base en la cual los estudiantes se podían apoyar para aprender y construir conocimiento. Era un orientador y no un simple transmisor de información en clase. Proponía ejercicios y consultas que invitaban a los estudiantes a desarrollar su capacidad de análisis, sin limitarse a desarrollar de manera mecánica ejercicios. Esto guarda relación con el supuesto de que el docente en las prácticas constructivistas debe ser un guía que fija objetivos, motiva a los estudiantes, promueve el autoaprendizaje, evalúa y a partir de estos tópicos retroalimenta y redirige los procesos constantemente (Zubiría, 2006).
De igual manera, buscaba la formación integral de los estudiantes. Se encargaba de propiciar espacios para la formación en aspectos adicionales a los matemáticos, como en valores y principios (Imagen 2). Se preocupaba por que cada uno estuviera en disposición de aprender. En este orden de ideas, era muy importante para él conocer el contexto en el cual estaba inmerso cada alumno, para ayudarlo en los problemas que pudiera tener, no solo en la asignatura, sino también en su vida personal.
Así, reflejaba con creces en cada clase las características que un profesor constructivista debe asumir: ser un mediador entre el conocimiento y el aprendizaje de sus estudiantes; ser un profesional reflexivo y crítico; promover aprendizajes significativos; prestar una ayuda pedagógica que se ajuste a los estudiantes y sus necesidades; respetar sus opiniones y a ellos; establecer una buena relación interpersonal con sus discípulos basada en valores que se intenten enseñar; y evitar convertirse en un simple transmisor de información o caer en la enseñanza unidireccional (Díaz & Hernández, 2005).
Imagen 2
Manuel Suárez y algunos de sus estudiantes

Nota. Manuel Suárez es el tercero de izquierda a derecha.
Rol del estudiante
El papel del discente era el de indagador. Siempre debía estar preguntándose por la veracidad de los contenidos, cómo llegar a ellos y cómo utilizarlos. Asumía una postura reflexiva que lo hiciera consciente de cada decisión o avance que se presentara en el aula. Esto lo resume su discípulo Germán Torres Roa, en las siguientes palabras: “El docente exquisitamente orientador y el alumno rigurosamente indagador” (G. Torres, entrevista personal, 10 de agosto, 2014).
El tiempo adicional a la clase que el estudiante debía dedicar era considerable. Siempre fue resultado de la motivación generada por el docente y no como una imposición. Cada estudiante decidía qué libros leer, qué ejercicios realizar y a qué ayudas recurrir. Eran conscientes siempre de que podían acudir a su profesor en el momento que lo necesitaran, sin importar el día de la semana que fuera. Incluso los festivos podían reunirse con él para dirigir correctamente su proceso de aprendizaje.
Generalmente, actividades individuales nunca dejaba. Dejaba temas y todo el mundo sabía que debía consultarlos y trabajarlos. Si alguien quería trabajar esos temas con él, los convocaba días diferentes de los horarios de clase, generalmente el sábado o fines de semana. No importaba. A veces el domingo trabajábamos. (A. Jiménez, entrevista personal, 27 de junio, 2014)
El papel del estudiante en los cursos dirigidos por el profesor Suárez guarda similitud con algunos aspectos asociados al constructivismo (Díaz & Hernández, 2005), como el hecho de que el aprendizaje es resultado de un proceso constructivo interno, autoestructurante, subjetivo y personal, el cual se facilita mediante la interacción con otros, es decir, en un proceso social y cooperativo de reconstrucción de saberes, donde además el autoconocimiento, las metas personales y la disposición por aprender se convierten en aspectos fundamentales para el éxito o fracaso del aprendizaje.
Interrelación entre el docente y el estudiante
Esta relación era de mucha cercanía gracias a la empatía natural y a las estrategias pedagógicas del docente (Imagen 3). La forma en que imponía su dinámica de clase permitía a los estudiantes pasar de sentir el temor y la inferioridad propios de la época, a tener seguridad y confianza completa en el aula. Con esto se propiciaban clases de comunicación multilateral en donde toda intervención era siempre respetada y valorada.
La incondicional disposición al diálogo que mostraba el profesor permitía a sus alumnos sentirse cómodos y sin temor de hablar con él, ya fuera de temas académicos o personales:
Él era una persona muy seria, pero a la vez muy dado a tener confianza con el estudiante. Nos hacía sentir libres para opinar, proponer y, en general, trabajar. Era una persona que siempre nos colaboraba en lo matemático y en lo personal. (F. Leguizamón, entrevista personal, 31 de julio, 2014)
Imagen 3
Manuel Suárez en ceremonia de grado de su estudiante Miguel Díaz Moreno (1979)

Imagen 4
Agradecimiento de estudiante en trabajo de grado

Nota. Agradecimiento de Publio Suárez Sotomonte. Tomado del trabajo Conjuntos trivialmente compactos (1989).
La estrecha relación que formaba con los estudiantes le permitió guiarlos a través de sus carreras de pregrado y posgrado, al vincularlos siempre con la investigación y la búsqueda de la enseñanza correcta de la matemática (Imagen 4). Disponía de su tiempo libre y de sus recursos para motivarlos a seguir adelante en su formación:
En un comienzo estudiábamos mucho en la casa de él. Teníamos grupo de estudio y lo frecuentábamos después de haber salido del pregrado. Incluso cuando estudiamos en la especialización en la UN, él fue nuestro cómplice permanente para poder nosotros adquirir el hábito de estudiar. (M. Díaz, entrevista personal, 17 de junio, 2014)
Recursos didácticos
Sin lugar a duda, una de las cosas más importantes para el profesor Manuel era ganar siempre la atención de sus estudiantes en la clase, razón por la cual, ante los escasos recursos de la época, se valía de la expresión corporal, del manejo de los colores en el tablero y, en algunas ocasiones, de acetatos ilustrativos. Sin embargo, estos aspectos no eran más que acompañantes para su principal herramienta con sello personal: los diagramas de flujo (Figura 2), en los cuales se desarrollaban desde definiciones o nociones de un tema, hasta demostraciones de teoremas o propiedades de topología.
Figura 2
Diagrama elaborado por Manuel Suárez
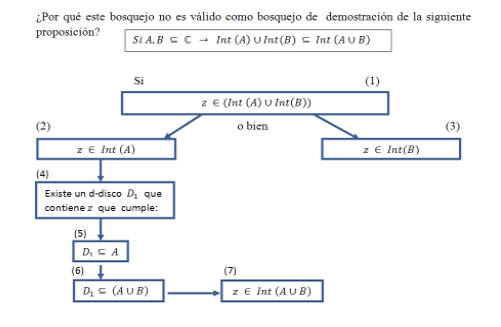
Nota. Diagrama elaborado por Manuel Suárez. Adaptado del libro Topología general. IV parte (Suárez, 1995).
Estos diagramas eran pensados por el profesor para desarrollar procesos de indagación. En efecto, él proponía una forma de iniciarlos y luego se avanzaba con ideas y aportes de los estudiantes. Al final de cada clase, quedaban diagramas que, por lo general, inundaban todos los tableros que existieran en el salón. Se procuraba no borrar nada de lo construido para que cada quien tuviera la oportunidad de detenerse o regresar a la parte del proceso que necesitara, de modo que, al revisar los apuntes de cada estudiante, se encontraban diagramas mucho más completos que los desarrollados por el profesor.
Cuando los cursos ya habían avanzado o cuando se pasaba al curso de Topología 2,
él no sólo planeaba las clases, sino que en distintas ocasiones delegaba en sus estudiantes el conocimiento previo del tema a tratar, delegando por turnos la elaboración de guías de trabajo para la apropiación del tema por parte del grupo. (G. Torres, entrevista personal, 10 de agosto, 2014)
Estas guías eran una oportunidad para mantener a los estudiantes más destacados activos y también una ayuda adicional para aquellos que por alguna razón quedaban relegados del avance de los temas.
Contenidos temáticos
El manejo de los contenidos temáticos de topología que aportaba el profesor era indiscutible y él se apoyaba en eso para organizar las clases y dosificar siempre los temas en tiempo, cantidad y dificultad, pero teniendo como prioridad su comprensión. Procuraba siempre que la relación entre el alumno y los conceptos topológicos fuera cada vez más independiente de él. El objetivo era que cada uno de los contenidos que se vieran en clase fuera el resultado de una elaboración conjunta de todos los que participaban en el aula y no una vertical imposición teórica. Pese a que la topología es una rama de las matemáticas muy formal, el profesor Manuel Suárez no asignaba prioridad a la cantidad o al orden estricto de los temas que se desarrollarían.
En realidad, él no se preocupaba mucho por los contenidos. Esa no era la filosofía de los cursos. No era plantear unos contenidos e intentar desarrollarlos. Lo importante era cómo se desarrollaban. Quedaba uno como estudiante sorprendido al ver cómo se alcanzaban muchos más temas de los que tenía el programa y con un aprendizaje realmente significativo. (M. González, entrevista personal, 15 de abril, 2014)
Evaluación
Se realizaban evaluaciones individuales de manera escrita, como parte de un proceso evaluativo más amplio, en el cual se tenía en cuenta toda la evolución del estudiante en la asignatura. Daba valor a la participación y al compromiso. Trasmitía la idea fundamental de que la evaluación no era más que una nueva oportunidad para aprender aún más. La nota de una evaluación no era un indicador para ningún estudiante de si sabía o no. Cada estudiante adquiría la convicción de cuáles eran sus falencias y de que en cualquier momento podía aprobar o no la materia.
Nadie sabía si iba a ganar o a perder, a pesar de que él devolvía las evaluaciones, explicando cuáles eran sus errores. En alguna ocasión, puso a habilitar a todo el grupo en Topología 2. Nos puso un día sábado todo el día habilitando. Cuando yo terminé y le entregué me dijo: “Usted no tenía que habilitar, pero tranquilo que eso es bueno”. Entonces en realidad él se preocupaba por que la gente estudiara. (A. Jiménez, entrevista personal, 27 de junio, 2014)
Resultados y conclusiones
Esta investigación es fundamentalmente un aporte a la memoria histórica de la UPTC, ya que Manuel Suárez marcó una época muy importante en el desarrollo de la Escuela de Matemáticas y Estadística de la universidad. Hacia el año 2000, Manuel Suárez recibió el Reconocimiento a la Calidad de la Investigación Científica en la IV Quincena de la Investigación de la UPTC. Ya en 2002, debido al cáncer que lo aquejaba, empezó a disminuir su trabajo investigativo y su labor docente. Se despidió definitivamente de la vida académica en 2004 con la condecoración Julius Sieber: Pedagogía y Ciencia en virtud de sus méritos, cualidades y contribuciones al desarrollo científico y educativo.
Entre los trabajos del profesor Suárez, se encontraron en total 19 registros de publicaciones ―5 libros y 11 artículos de revista, un informe de proyecto de investigación, así como los libros de sus trabajos de grado en especialización y maestría―, 30 ponencias en eventos tanto en Colombia como en el exterior y 19 trabajos de grado dirigidos.
A todas luces, más allá de los notables teoremas y desarrollos matemáticos alcanzados por el profesor Suárez, su más valioso legado radica en la formación de docentes, pues debido al éxito de sus clases, quienes fueron sus estudiantes (figura 3) terminaron por ser docentes exitosos. Algunos de ellos han impulsado el avance de la Escuela de Matemáticas y Estadística y el programa de Licenciatura en Matemáticas de la UPTC.
Entre las prácticas de aula que sus discípulos han conservado se destacan: el manejo de grupo, tiempos y espacios del aula, el cuestionamiento permanente al estudiante, la buena preparación teórica de los temas y la búsqueda constante de estrategias para luego enseñarlos, el uso de herramientas gráficas como mapas y diagramas, la generación de un ambiente de aula agradable que permita mantener una relación cordial y cercana con los estudiantes, la evaluación permanente e integral, así como el compromiso y dedicación para la construcción del conocimiento mediante la investigación como parte del proceso de aprendizaje, como lo expresa Jiménez (2005):
Para la enseñanza de la Matemática, seguí la disciplina de estudio y hasta las estrategias de clase usadas por mi profesor de Matemática de la Universidad, Manuel Suárez Martínez. Vale la pena destacar que era el único que hacía la clase en forma diferente de “solo llenar el tablero”, y quien marcaría mi futuro profesional. Usaba los procesos deductivos, a partir de un sinnúmero de ejemplos variados, para llegar a los conceptos y definiciones; exigía rigor extremo en los procesos de la Matemática, pero, al mismo tiempo interactuaba suficientemente con sus alumnos y buscaba que ellos viviesen, de alguna forma la matemática. (pp. 23-24)
Figura 3
Trabajos de grado dirigidos por Manuel Suárez
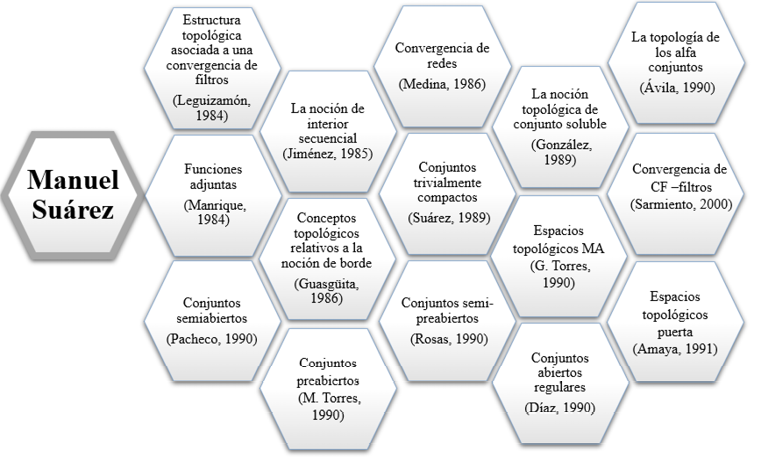
Nota. Trabajos de grado dirigidos en la Especialización en Matemática avanzada y la Maestría en Matemáticas.
Con el interés por enseñar una matemática más humana, Manuel Suárez rompió con la tendencia tradicionalista de la enseñanza que se imponía en la época en que inició su desempeño como docente. Fue el formador de una nueva generación de formadores, que adquirieron una concepción distinta de la matemática y su enseñanza. Además, fue el precursor y pionero de la vinculación de la investigación a las clases de matemática en la UPTC, al crear formalmente su primer grupo colaborativo de investigación en topología, con el que se obtuvieron diversos resultados topológicos y se formaron docentes investigadores que han liderado durante años el desarrollo de la matemática y de la educación matemática en el departamento de Boyacá.
Referencias
Amaya, R. (1991). Espacios Topológicos Puerta Tesis de Especialización no publicada]. Universidad Nacional de Colombia en convenio con la Universidad Pedagógica y Tecnológica de Colombia.
Ávila, A. (١٩٩٠). La topología de los alfa-conjuntos [Tesis de Especialización no publicada]. Universidad Nacional de Colombia en convenio con la Universidad Pedagógica y Tecnológica de Colombia.
Camacho, R., & Suárez, M. (1987). La función topológica de exterior. UPTC.
Coll, C. (1990). Constructivismo y educación: la concepción constructivista de la enseñanza y del aprendizaje. En C. Coll, J. Palacios, & A. Marchesi (Comps.), Desarrollo psicológico y educación II: Psicología de la educación escolar (pp. 29-66). Alianza.
Corbin, J., & Strauss, A. (2002). Bases de la investigación cualitativa. Técnicas y procedimientos para desarrollar la teoría fundamentada. Universidad de Antioquia.
Díaz, F., & Hernández, G. (2005). Estrategias docentes para un aprendizaje significativo. Una interpretación constructivista. Mc Graw-Hill.
Díaz, M. (1990). Conjuntos abiertos regulares [Tesis de Especialización no publicada]. Universidad Nacional de Colombia en convenio con la Universidad Pedagógica y Tecnológica de Colombia.
Gómez, C., & Suárez, M. (1992). Conjuntos fronterizos. Boletín de Matemáticas y Estadística, 2(1), 1-23.
González, M. (1989). La noción topológica de conjunto soluble [Tesis de especialización no publicada]. Universidad Nacional de Colombia en convenio con la Universidad Pedagógica y Tecnológica de Colombia.
Guasgüita, J. (1986). Conceptos topológicos relativos a la noción de borde [Tesis de Maestría no publicada]. Universidad Pedagógica Nacional.
Jiménez, A. (1985). La noción de interior secuencial [Tesis de Especialización no publicada]. Universidad Nacional de Colombia en convenio con la Universidad Pedagógica y Tecnológica de Colombia.
Jiménez, A. (2005). Formación de profesores de matemática: Aprendizajes Recíprocos escuela-universidad. Búhos Editores.
Leguizamón, J. (1984). Estructura topológica asociada a una convergencia de filtros [Tesis de Especialización no publicada]. Universidad Nacional de Colombia en convenio con la Universidad Pedagógica y Tecnológica de Colombia.
Lineros, C., & Suárez, M. (1999). Estructuras sintopógenas y topologías [Conferencia]. III Congreso Iberoamericano de Topología, Gandía, España.
Manrique, H. (1984). Funciones adjuntas [Tesis de Especialización no publicada]. Universidad Nacional de Colombia en convenio con la Universidad Pedagógica y Tecnológica de Colombia.
Medina, A. (1986). Convergencia de redes [Tesis de Especialización no publicada]. Universidad Nacional de Colombia en convenio con la Universidad Pedagógica y Tecnológica de Colombia.
Pacheco, C. (1990). Conjuntos semiabiertos [Tesis de Especialización no publicada]. Universidad Nacional de Colombia en convenio con la Universidad Pedagógica y Tecnológica de Colombia.
Redacción El Tiempo. (6 de septiembre 2000). La vida entre números. El Tiempo. http://www.eltiempo.com/archivo/documento/MAM-1277048.
Rosas, D. (1990). Conjuntos semi-preabiertos [Tesis de Especialización no publicada]. Universidad Nacional de Colombia en convenio con la Universidad Pedagógica y Tecnológica de Colombia.
Ruiz, C., & Suárez, M. (1975). Elementos de topología (cuaderno 1). Departamento de Matemáticas, UNAL.
Ruiz, C., & Suárez, M. (1976). Elementos de topología (cuaderno 2). Departamento de Matemáticas, UNAL.
Ruiz, C., & Suárez, M. (1980). Topología o convergencia (Fascículo 2) [Conferencia]. X Coloquio Colombiano de Matemáticas. Paipa. Colombia.
Ruiz, C., & Suárez, M. (1995). Hacia una revisión de la topología conjuntista: utilizando como referentes a O. Ore, G. Boole, F. Klein, K. Kuratowski y J. Adamek. [Conferencia]. I Congreso Iberoamericano de Topología y sus Aplicaciones, Benicassim, Valencia, España.
Sarmiento, E. (2000). Convergencia de CF-filtros [Tesis de Maestría no publicada]. Universidad Nacional de Colombia.
Suárez, H., Maluendas, P., & Serna, J. (2021). Topología: un curso introductorio. Vol. I. Editorial UPTC.
Suárez, M. (1988). La función topológica Hunza [Tesis de Especialización no publicada]. Universidad Nacional de Colombia en convenio con la Universidad Pedagógica y Tecnológica de Colombia.
Suárez, M. (1989). La función topológica Hunza [Conferencia]. The Northeast Conference on General Topology and Applications, Nueva York, Estados Unidos.
Suárez, M. (1990). Funciones adjuntas en topología general [Conferencia]. I Coloquio Bolivariano de Matemáticas, Quito, Ecuador.
Suárez, M. (1991). Topologías asociadas con el álgebra de Boole PX [Conferencia]. Topologies associated with the Boolean algebra P(X), Madison, Estados Unidos.
Suárez, M. (1992a). Topología Conjuntista: Una presentación booleana adjunta. IX Coloquio Distrital de Matemáticas y Estadística. Universidad Distrital Francisco José de Caldas.
Suárez, M. (1992b). Un ejemplo de álgebra booleana. Boletín de Matemáticas y Estadística, 1(1), 11-15.
Suárez, M. (1993a). Álgebras booleanas de cuantificadores. Ciencia en Desarrollo, (1), 130-136.
Suárez, M. (1993b). Topología conjuntista: una presentación booleana adjunta (Continuación). X Coloquio Distrital de Matemáticas y Estadística. Universidad Distrital Francisco José de Caldas.
Suárez, M. (1994). El grupo de Klein y la teoría de adjunción en la topología conjuntista [Tesis de Maestría no publicada]. Universidad Nacional de Colombia.
Suárez, M. (1995). Topología general. IV parte. Universidad Pedagógica y Tecnológica de Colombia.
Suárez, M. (2001). La noción topológica de m-filtro [Conferencia]. Cuarto Congreso Iberoamericano de Topología y sus Aplicaciones, Coímbra, Portugal.
Suárez, M. (2003). Spring Topology and Dynamical Systems [Conferencia]. Joint Maps and Supratopologies, Texas, Estados Unidos.
Suárez, M., & Suárez, P. (1997). Conjuntos trivialmente compactos [Conferencia]. II Congreso Iberoamericano de Topología, Morelia, México.
Suárez, M., & Torres, G. (1982). Criterios de convergencia secuencial. Revista Colombiana de Matemáticas, (16), 81-94.
Suárez, M., & Torres, G. (1990). Funciones de núcleo o topologías. Revista Integración, 8(2), 179-200.
Suárez, M., & Torres, G. (1992). Funciones de fundamental o topologías booleanas. Boletín de Matemáticas y Estadística, 11(1), 23-49.
Suárez, P. (1989). Conjuntos trivialmente compactos [Tesis de Especialización no publicada]. Universidad Nacional de Colombia en convenio con la Universidad Pedagógica y Tecnológica de Colombia.
Torres, G. (1990). Espacios topológicos MA [Tesis de Especialización no publicada]. Universidad Nacional de Colombia en convenio con la Universidad Pedagógica y Tecnológica de Colombia.
Torres, M. (1990). Conjuntos Preabiertos [Tesis de Especialización no publicada]. Universidad Nacional de Colombia en convenio con la Universidad Pedagógica y Tecnológica de Colombia.
Zubiría, S. (2006). Los modelos pedagógicos: hacia una pedagogía dialogante. Cooperativa Editorial Magisterio.






